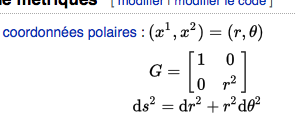Bonjour,
J'ai une question concernant le produit scalaire.
Tout d'abord:
Soit a un vecteur appartenant à un espace vectoriel de dimension 2. a(x,y)
Imaginons ce vecteur dans un repère orthonormée. Sa norme est donnée par la relation de pythagore.
Désormais ce vecteur est transformée dans un repère sphérique .
Je peux trouver sa norme en utilisant:
Le tenseur métrique étant intervenu.
Maintenant traçons un triangle sur un plan. Si je transforme le plan en cylindre , alors j'obtiens un espace localement euclidien.
Mais si je le "transforme en sphère" , la somme des angles du triangles n'est plus égale à 0...
Si je réalise le produit scalaire de deux vecteurs du triangle sur le plan , j'obtiens D.
Si le produit scalaire est invariant , et que mon angle entre deux vecteurs du triangle a varié ( sur la sphère) alors les normes des deux vecteurs ont également variées...
Mes questions sont donc:
Le produit scalaire est-il invariant quand on passe d'un espace euclidien à un espace non-euclidien?
Si oui, je ne comprends pas pourquoi la norme change..., la distance doit restée à mes yeux invariantes... ( en rg, on peut observer des contractions de longueurs mais cette longueur est mesuré par un observateur immobile par rapport à un référentiel en mouvement...)
-----