Coefficient angulaire d'une droite simultanement tangente a deux droites

[ThoriumUranium]

Bonjour,

Je dois trouver un nombre A qui est le coefficient angulaire d'une droite tangente aux deux paraboles y=x²+1 et y= -1-(x-1)²

Je ne me souviens plus de la méthode de résolution d'un tel problème, Pourriez vous m'aider?

Merci beaucoup
-----

[gg0]

Bonjour.

Il y a plusieurs méthodes possibles pour traduire la tangence :
* dire que le droite et la parabole se coupent en un point double
* passer à la limite sur les intersections droite/courbe
* utiliser la dérivée (qui donne d'ailleurs le coefficient angulaire).

A toi de choisir. A priori, on va utiliser une équation y=ax+b de la droite, avec a et b inconnus.

Cordialement.

[ansset]

Bonjour.

Il y a plusieurs méthodes possibles pour traduire la tangence :
* dire que le droite et la parabole se coupent en un point double
* passer à la limite sur les intersections droite/courbe
* utiliser la dérivée (qui donne d'ailleurs le coefficient angulaire).

A toi de choisir. A priori, on va utiliser une équation y=ax+b de la droite, avec a et b inconnus.

Cordialement.

la première me semble la plus "naturelle" ( ps : il y a deux paraboles )
attention : il y a au final deux solutions.

[Merlin95]

Bonjour,

Qu'est-ce que vous entendez par "se coupent en un point double", et il y a deux paraboles donc je n'ai pas compris la méthode.
Perso, je ne vois pas de méthodes plus puissantes que de passer par les dérivées.

[A voir en vidéo sur Futura]

[ansset]

je n'ai pas dit cela; j'ai dit qu'il y avait deux tangentes différentes communes aux deux paraboles.

soit f(x) la fonction correspondant à une parabole ( un polynôme du 2nd degré ici )
les intersections de toute droite y(x)=ax+b avec cette parabole revient à
f(x)=ax+b ce qui revient à
f(x)-(ax+b)=0 qui a donc 0,1, ou 2 solutions
Une tangente à la courbe correspond de fait à un discriminant de
P(x)=f(x)-(ax+b) nul ( double racine donc un point d'intersection unique )

dans le premier cas: y=x²+1
P(x)=x²-ax+1-b
Delta=a²-4(1-b)=0
soit a²=4(1-b)
tout couple ( a;b) vérifiant cette équation est tangente à la courbe quelque part.

deuxième cas
-1-(x-1)²-ax-b=0 soit
-x²+(2-a)x-(1-b)=0
Delta nul => (2-a)²=4(2-b)

Une droite qui soit tangente aux deux paraboles doit donc satisfaire ces deux équations
On en tire une équation du second degré en a
2a²-4a-4=0
ce qui donne 2 solutions pour a et donc pour les droites ax+b tangentes aux deux paraboles à la fois.( b dépendant de a ).

De mon coté, je ne vois pas directement comment trouver ces droites en partant simplement des dérivées.

[Merlin95]

Je ne m'adressais pas à toi en premier lieu, je rebondissais sur ca :

* dire que le droite et la parabole se coupent en un point double

Mais merci c'est plus clair.

[ansset]

c'est une autre manière de dire que l'intersection ne se fait qu'en un seul point ( qui est la double racine que j'évoque)

[ansset]

je corrige ce que j'ai dit plus haut , on s'en sort aussi assez bien avec les dérivées, mais..... "j'aime moins" ( question de goût )

[Merlin95]

Pour les dérivées, on a les points des deux paraboles P et P' où passent la même tangente.

A ces, les dérivées sont égales, on donc soit

on écrit l'équation de la droite à ces deux points :




soit en remplaçant x'0 par 1 - x0, un système à deux inconnues deux équations




soit



d'où




D'où deux solutions pour et on en déduit le coefficient directeur

[ansset]

ptite correction , désolé :

deuxième cas
-1-(x-1)²-ax-b=0 soit
-x²+(2-a)x-(1-b)=0

erreur, le calcul juste donne :
-x²+(2-a)x-(b+2)
d'où après

Une droite qui soit tangente aux deux paraboles doit donc satisfaire ces deux équations
On en tire une équation du second degré en a
2a²-4a-4=0

Devient :
a²-2a-4=0

les deux valeurs de a sont donc
1 +/- rac(5)

[ansset]

Ci-joint le graphique, si j'y parviens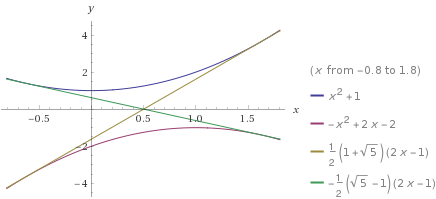

[Merlin95]

Pour conclure mon message précédent, c'est bien ce que je trouve

[ansset]

Je trouve effectivement le même résultat avec les dérivées ( c'est heureux ) , avec une démarche assez proche..

[ansset]

en prenant les deux points "tangentiels" (x1;y1) (x2;y2 )
j'ai écris comme toi au début
a=2x₁=-2x₂+2 d'où l'écriture de x₁ et x₂ en fct de a
puis
f(x₂)-f(x₁)=a(x₂-x₁)
en remplaçant les x_i par leurs expressions en a , on obtient l'équation du second degré en a.

[Merlin95]

C'est en effet à peu près la même méthode.