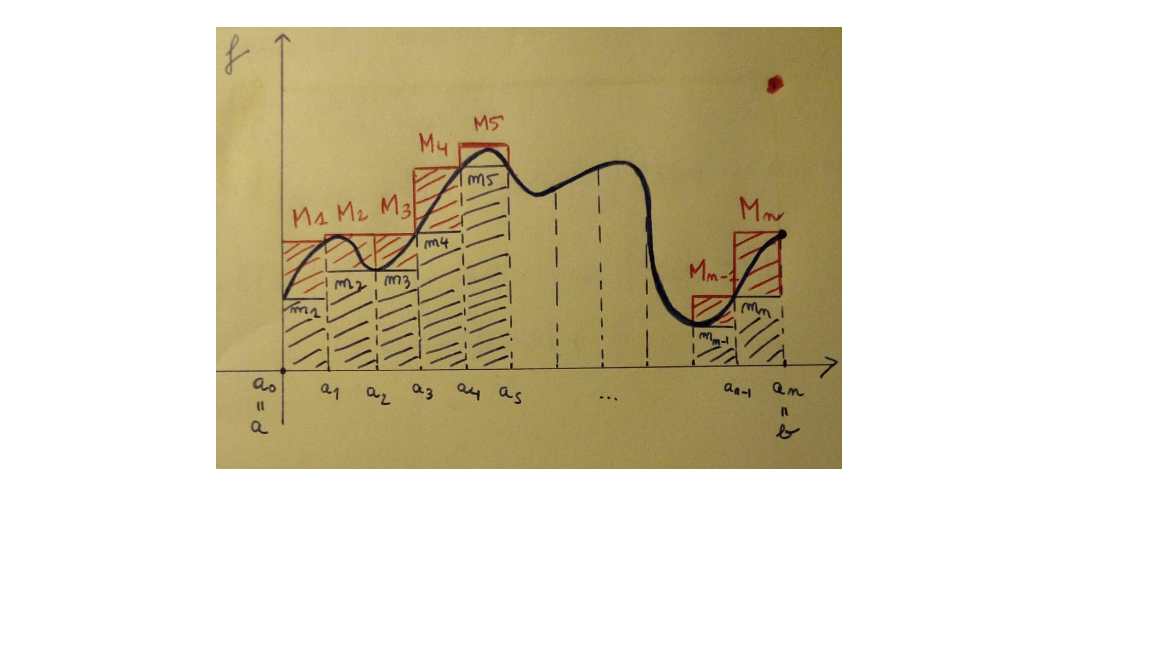
Fonction continue approchée par des fonctions en escaliers
Discussions similaires
-
Par andretou dans le forum Mathématiques du supérieur
Réponses: 94
Dernier message: 26/01/2018, 11h05
-
Par kaderben dans le forum Mathématiques du collège et du lycée
Réponses: 3
Dernier message: 16/04/2014, 21h02
-
Par invite2b14cd41 dans le forum Mathématiques du supérieur
Réponses: 8
Dernier message: 25/01/2011, 00h07
-
Par invite553bd433 dans le forum Mathématiques du supérieur
Réponses: 1
Dernier message: 29/03/2010, 14h13
-
Par Seirios dans le forum Mathématiques du supérieur
Réponses: 14
Dernier message: 10/12/2009, 22h25
et
à la place de b ?
fermés en
et ouverts en
?