Suites convergente, définition limite ...

[invitecb3dc26d]

Bonjour,

Je rencontre un énorme problème, je n'arrive pas à résoudre ce type d'exercices. Je ne cherche pas à avoir la correction, étant donné que je l'ai déjà, mais plus d'un "accompagnement". J'ai besoin de vos conseils, vos suggestions de méthodes et tout ce qui pourrait me servir pour surmonter ces lacunes en analyse.

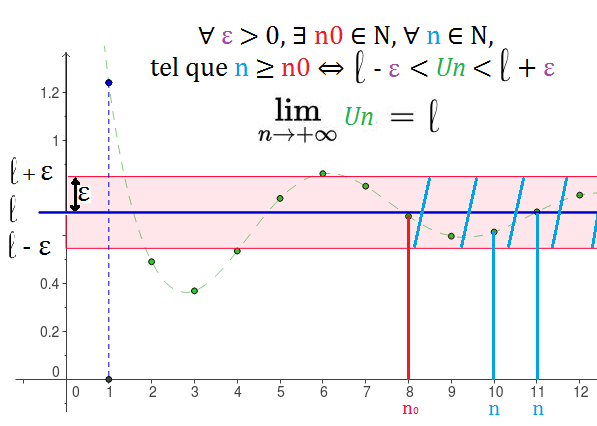
D'après ce qu'on m'a dit, avec la définition de la limite, je peux résoudre tous ces exercices, qui est :
∀ ε > 0, ∃ No ∀ n > No, |Un - l | < ε

Le problème, c'est que je me suis représenter cette définition avec un schéma(Comme j'ai pu faire et comprendre avec le TVI et les bornes atteintes) etc, tout ce que j'ai pu, je n'arrive pas à la comprendre réellement / parfaitement (Bien que je sache calculer certaines limites).

Donc je ne sais plus quoi faire, j'ai besoin d'aide s'il vous plaît.




Merci beaucoup,
Bonne journée,
-----

[albanxiii]

Bonjour,

Pour les exercices du type 1.2, il faut d'abord essayer de se demander si l'affirmation est vraie, et si on a des doutes il est amusant d'essayer de trouver des contre exemples simples.

Par exemple, pour la question 1, est-ce que vous pouvez trouver une suite positive dont certains termes deviennent de plus en plus grands et dont d'autres non ? Si vous pouvez, cette suite n'est pas majorée (quel que soit le nombre A>0 qu'on choisit, on peut trouver des termes de la suite qui sont plus grands), et si les termes "grands" et "pas grands" sont alternés, on ne peut pas dire que la suite tends vers + l'infini (puisque certains termes ne satisfont pas la définition de la limite dans ce cas). Personnellement, je trouve ce genre de contre exemple en visualisant.

Pour la 4, c'est du même tonneau, pensez à une suite dont les termes deviennent de plus en plus grands mais qui changent de signe régulièrement.

Exercice 1.5 : intuitivement, la suite u_n tend vers l, cela veut dire qu'à partir d'un certain rang les termes de la suite seront peut différents de l. Donc en gros, pour n grand, vous aurez beaucoup de termes proches de l au numérateur. Le tout divisé par n, ça doit donner quelque chose de proche de l.
Pour le formaliser, on peut penser à découper la somme en deux, les u_n avant n=N_à et ceux après, le N_0 étant choisi de sorte que pour n > N_0 le terme u_n est justement proche (à epsilon près) de l. Puis regardez comment évolue chaque groupe quand n devient grand (je n'ai rien inventé, votre exercice c'est le théorème de Césaro, le raisonnement est classique et il repose sur le fait que "l'infini c'est grand").

Pour la question 2, il est facile de trouver un contre exemple, en se souvenant qu'une suite divergente n'est pas forcément une suite qui tend vers l'infini.

Je vous laisse avec ça, d'autres compléteront et expliqueront autrement.

[gg0]

Bonjour Ingenil.

Je pointe la question 3 de l'exercice 1.2, qui est un résultat utile. La représentation géométrique d'une suite de limite l finie (*) permet de voir que c'est vrai, puisque pour tout n suffisamment grand, les Un seront plus près de l que 0.
La question 5 du même exercice est un peu un piège, car on a tendance à évacuer la question de la convergence. Il faut voir qu'on ne dit rien de la succession des Un, tout ce qui est dit est valable pour chaque n, seulement pour ce n.

Pour l'exercice 1.6, la définition ne suffira pas. Il est nécessaire d'apprendre tout le cours sur les suites, pour avoir des outils efficaces.

Cordialement.

(*) si la limite est infinie, la représentation est différente

[invitecb3dc26d]

Bonjour,


Le problème c'est que je n'arrive pas à visualiser les choses, même en cherchant des contre exemple je n'y arrive pas, ce genre de chapitre c'est vraiment mon point faible. Même en cherchant les contres-exemples il n y a rien qui sort de ma tête... (En plus je crois qu'il faut aussi des preuves et qu'un exemple ne suffit pas) et la définition de la limite je ne la comprend pas


Pour la question 1 il y a peut-être U(n) = (-1)^n, cette suite est non-majoré et elle ne tend pas vers +oo. Le seul problème c'est qu'il demande une suite positive et elle n'est pas postive puisqu'elle oscille entre valeur négative et positive

[A voir en vidéo sur Futura]

[gg0]

Pour tous ces exercices, il faut avoir calculé à la main, calculé beaucoup, essayé au brouillon, et pensé à tout ce qui s'est passé.
Et ne pas se laisser bloquer par la première petite difficulté, chercher encore.
Par exemple pour ton U(n) = (-1)^n, il suffit de pas grand chose pour que ça marche, mais tu n'as pas cherché. Comment faire pour qu'il n'y ait plus de valeurs négatives (qui sont quoi ?).
Il n'y a pas de miracle, seul la travail, la réflexion, l'essai de solutions (même si à la fin ça ne marche pas), ... te feront progresser.

Pour la définition de limite (finie), rien d'extraordinaire. Elle dit qu'à condition d'aller assez loin dans la suite (n>N0) tous les termes de la suite seront désormais très près de l; en fait, aussi près que l'on veut (puisque epsilon peut être choisi quelconque dans les strictement positifs, en particulier très proche de 0). Rappel : la limite d'une suite, c'est vu en lycée, et, à ce moment-là, le prof explique ce qu'on veut faire.

Cordialement.

[PlaneteF]

Bonsoir,

Pour la question 1 il y a peut-être U(n) = (-1)^n, cette suite est non-majoré

Ben non, cette suite est bel et bien majorée

Cordialement

[PlaneteF]

(En plus je crois qu'il faut aussi des preuves et qu'un exemple ne suffit pas)

Un seul contre-exemple suffit pour démontrer qu'une proposition est fausse. Par exemple si la proposition est "tous les corbeaux sont noirs", et bien le simple fait d'exhiber un seul corbeau qui serait d'une autre couleur, suffit à montrer que cette affirmation est fausse

Cordialement

[gg0]

En complément, Ingénil, rappelle-toi qu'une suite c'est n'importe quoi, au sens où un peut être à priori n'importe quel nombre. Tu as la liberté d'écrire tout ce que tu veux pour la valeur de Un, même une valeur prise au hasard à chaque terme.
2; 3,14; -56; 45848747; 0; 0; 0; 0; 548745,25478 est le début d'une suite, d'une infinité de suites plutôt, puisque on a les termes de U0 à U8 et qu'on peut mettre n'importe quoi pour U9, et encore n'importe quoi pour U10, etc.

Cordialement.

[azizovsky]

il suffit de bosser pour avoir une sorte d'idées mathématiques expérimentales, d'après l'histoire, Ramanujan était un grand bosseur ....
une idée expérimentale sur la limite d'une suite u(n)=1/2^n : si on coupe un carré de coté 1 en deux (dessin pour visualiser ) puis en deux , puis ....à l'infini

on'a : 1/2 +(1/2)/2+((1/2)/2)/2+.....=1/2+1/4+1/8+....

sur le schéma, le 1/2 va couvrir la moitié du carré, puis on rajoute le quart, puis le 8 ème , ....., à la limite , on voit (dessin) que à la limite , qu'on va couvrir tous le carré de surface 1, donc la limite est 1 et à la limite |u(n)-1|<epsilon .

https://www.google.be/search?q=dessi...psD0BtNYECTRM:

[jacknicklaus]

procédons dans l'ordre.

l'exercice 1.2

le 1 : Bien comprendre que "tendre vers +infini" signifie que quelque soit un grand nombre A choisi, il y a un rang de la suite tel que TOUTES les valeurs de la suite au delà de ce rang sont plus grandes que le nombre A choisi. On va jouer sur le TOUTES pour trouver un contre-exemple.

peux-tu trouver une suite positive, telle que les termes pairs tendent vers +infini (ce qui assure le non majoré), mais dont les termes impairs sont majorés, ce qui interdit de "tendre vers l'infini" ?

[invitecb3dc26d]

Par exemple pour ton U(n) = (-1)^n, il suffit de pas grand chose pour que ça marche, mais tu n'as pas cherché. Comment faire pour qu'il n'y ait plus de valeurs négatives (qui sont quoi ?).

Question 1 : Faux

Comme U(n) = (-1)^n est borné [Elle a pour minorant -1 et pour majorant 1] on ne peut pas prendre cette suite, vu qu'on cherche une suite non majoré. Mais pour que cette suite n'est plus de valeur négatives il faudrait prendre U(n) = (-1)^2n et maintenant on a une suite positive et non majorée, le seul problème qu'il reste c'est qu'elle tend vers +oo

Sinon { U(n) = (-1)^n si n est pair
{ U(n) = (-1)^n + 3 si n est impair


Sinon il y a U(n) = cos(n) + 2 mais bon...

Question 2 : Faux


La suite : U(n) = 1/n

Question 3 : Vrai


Il faut seulement écrire la définition de la limite qui est contradictoire à l'assertion




Question 4 : Vrai

Dans le cours "Si une suite est non bornée, elle ne peut pas converger, donc elle diverge"

La suite : U(n) = (-1)^n * n est non bornée et elle est diverge

Question 5

Quand je vois cette assertion ça me fait penser au théorème des suites adjacentes, mais on m'a dit qu'il ne fallait pas se laisser avoir et que ça n'avait aucun sens.

Les suites (un) et (vn) sont dites adjacentes si (un) est croissante et (vn) est décroissante et lim (vn - un) = 0
+ deux suites adjacentes convergent et ont même limite.

Question 6

...

[gg0]

Bonjour.

Question 1 : C'est effectivement faux. Mais je ne comprends pas tout ce que tu racontes. Comment faut-il interpréter ton écriture "(-1)^2n" ??? Tu ferais l'effort de regarder ce que signifient tes écritures, on pourrait savoir de quoi tu parles et tu apparaîtrait un peu plus intelligent. Exemple :
"(-1)^n si n est pair" Tu n'as jamais essayé de penser ce qu'est une puissance paire de -1 ?? Jamais ? Pourtant, tu as appris en début de collège, une règle qui en parle, la règle des signes. Mais tu ne cherches pas à savoir ce que ont les 1, multipliés entre eux.
tu devrais, pour commencer à être raisonnable, écrire les 20 premiers termes de la suite (-1)^n.

Finalement, dans cette première question, tu ne proposes que deux exemples : "U(n) = (-1)^n si n est pair; U(n) = (-1)^n + 3 si n est impair" et "U(n) = cos(n) + 2 ", qui sont des suites positives, mais majorées, donc qui ne contredisent pas la phrase proposée.

Question 2 :
Pourquoi parles-tu de cette suite décroissante ? Tu dis "faux", puis tu présentes un exemple qui confirme la phrase !!

J'arrête là, tu n'as pas voulu réfléchir sérieusement à ces questions très élémentaires, tu écris des expressions sans te soucier de ce qu'elles valent, inutile de continuer sur du plus difficile. Tant que tu n'auras pas essayé d'être intelligent, de comprendre de quoi tu parles et ce que tu écris, on perd son temps .

[PlaneteF]

Question 3 : Vrai


Il faut seulement écrire la définition de la limite qui est contradictoire à l'assertion

… Tu réponds que c'est vrai, puis tu parles de contradiction entre la proposition et la dédinition. Qu'est-ce que tu racontes ?

Si tu penses que c'est vrai, et bien démontre le !

Question 4 : Vrai

Dans le cours "Si une suite est non bornée, elle ne peut pas converger, donc elle diverge"

La suite : U(n) = (-1)^n * n est non bornée et elle est diverge

La 2e phrase sert à quoi ?

Question 5

Quand je vois cette assertion ça me fait penser au théorème des suites adjacentes, mais on m'a dit qu'il ne fallait pas se laisser avoir et que ça n'avait aucun sens.

Les suites (un) et (vn) sont dites adjacentes si (un) est croissante et (vn) est décroissante et lim (vn - un) = 0
+ deux suites adjacentes convergent et ont même limite.

Contre-exemple simple à trouver

Question 6

...

Contre-exemple très, très simple à trouver


Cordialement

[invitecb3dc26d]

Question 1 :

Faux, on a la suite

{ U(n) = n si n est pair
{ U(n) = 0 si n est impair

Elle est croissante et non majorée, mais elle ne tend pas vers +oo car les impairs reviennent en 0

Question 2 :

Faux, on a |cos(n)| / n

Question 3 :

Vrai. Dans cette assertion, je pense qu'il faut j'utilise la définition de limite avec epsilon assez petit pour m'assurer que tous les termes sont dans la bande et je peux dire que leur distance à 0 est strictement positive car la distance de la bande l'est. Par contre, je ne sais pas comment traduire ça mathématiquement...

Question 4


Vrai. Ici je peux me permettre de juste cité le cours "Si une suite est non bornée, elle ne peut pas converger, donc elle diverge"", je ne sais pas comment justifiez autrement car pour moi non-bornée -> divergente et bornée -> convergente

Pour la question 5 je pense que c'est faux et pour la question 6 je pense il faut utiliser la définition de la limite. Très simple à trouver peut-être mais je n'y arrive pas

Merci

[PlaneteF]

Question 1 :

Faux, on a la suite

{ U(n) = n si n est pair
{ U(n) = 0 si n est impair

Elle est croissante et non majorée, mais elle ne tend pas vers +oo car les impairs reviennent en 0

Non cette suite n'est pas croissante, … tu voulais dire "positive" ?

Question 2 :

Faux, on a |cos(n)| / n

Ce contre-exemple fonctionne peut-être mais est-ce si évident que cela ? Autant on sait comment se comporte cos(x) avec x réel, autant cos(n) avec n entier, comme ça à froid, intuitivement ça doit peut-être le faire, mais ce n'est pas si systématique que cela.

Tu peux trouver un contre-exemple bien plus simple

Question 3 :

Vrai. Dans cette assertion, je pense qu'il faut j'utilise la définition de limite avec epsilon assez petit pour m'assurer que tous les termes sont dans la bande et je peux dire que leur distance à 0 est strictement positive car la distance de la bande l'est. Par contre, je ne sais pas comment traduire ça mathématiquement...

Ecris la défintion de la limite en choisissant par exemple , et regarde ce que cela donne

Cordialement

[invitecb3dc26d]

Pour la question 1 : Oui positive pardon.
Pour la question 2 : J'ai pris du temps pour trouver cette suite sans trouver une autre (plus simple/plus difficile), mais si ça marche c'est ce qu'on veut, tant mieux

[invitecb3dc26d]

A moins :

{ Un = 1/2 si n est impair
{ Un = 0 si n est pair

mais bon

[gg0]

Tu parles de quelle question ???

[invitecb3dc26d]

J'ai déjà donné une réponse pour les questions 1, 2, 4. Pour la question 2, il m'a dit que ma réponse : |cos(n)| / n fonctionné peut-être, mais que je pouvais en choisir une plus simple. J'ai donné

{ Un = 1/2 si n est impair
{ Un = 0 si n est pair

[gg0]

Heu ... c'est une suite qui tend vers 0 ????

[invitecb3dc26d]

1/n * j'ai écrit 2 à la place de n j'avais pas vu

{ Un = 1/n si n est impair
{ Un = 0 si n est pair

[gg0]

OK. Cette fois c'est bon.

[PlaneteF]

@Ingenil,

Ton idée de "jouer" avec le cosinus était bien, tu pouvais tout simplement prendre :

Cordialement