Bonjour,
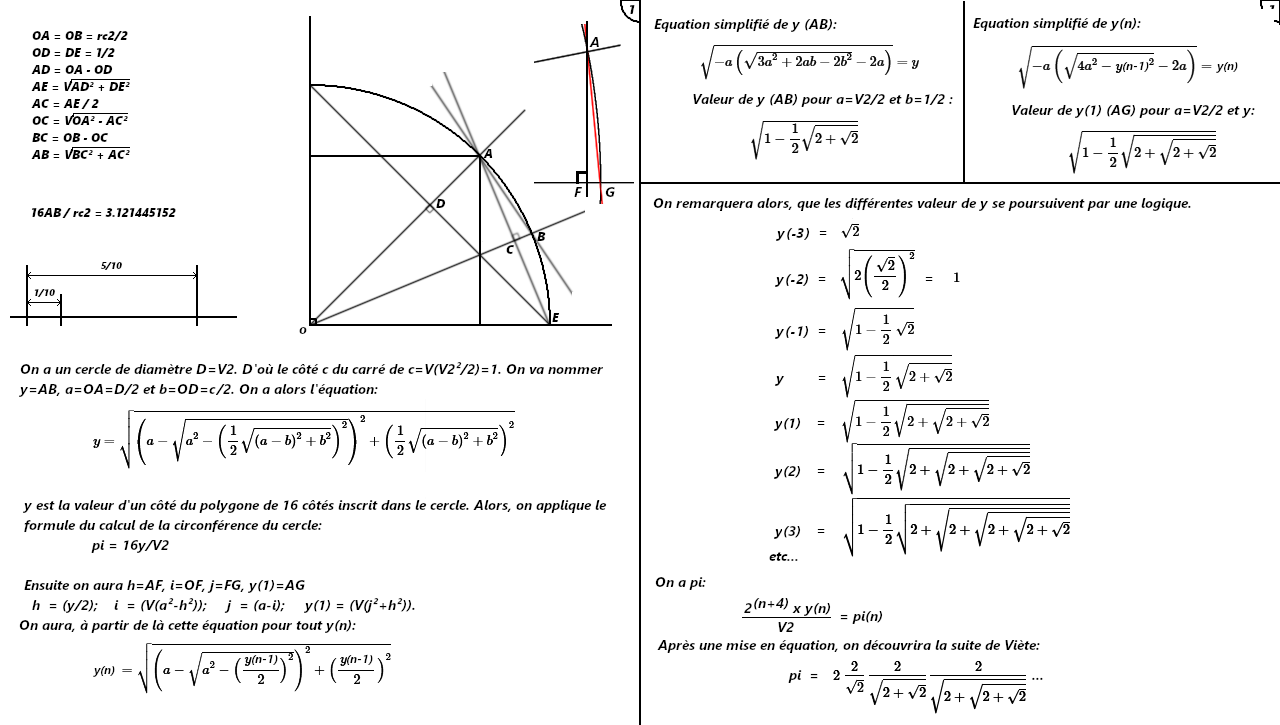
Je fait un peu de math et de géométrie en loisir, et je voudrais résoudre la suivante. Cela concerne pi (ben oui, en loisir). C'est moi qui est créé cette feuille, mais je n'arrive tout de même pas à résoudre ce problème. J'ai pourtant fait le programme sur un vieux Thomson et je trouve bien pi.
Si quelqu'un pourrait me faire le développement, je lui en serais reconnaissant.
Formules de base:
sin(2x)=2sin(x)cos(x); cos(2x)=2cos^2(x)-1
en en déduit:
maintenant on pose les suites :
etc (l'écriture LaTeX est vraiment fastidieuse...
dans le second membre on trouve n facteurs et le dernier contient au dénominateur n radicaux imbriqués.
comme
quand x tend vers 0 :
on obtient pour n grand, après avoir tout multiplié par 2x2^n :
J'espère que vous comprendrez et que cela correspond à ce que vous cherchez. Mes formules sont légèrement différentes des votres mais cela revient au même. Félicitation pour votre intérêt pour les mathématiques.
Bonjour,
C'est pas vraiment ce que j'attends. Je voudrais vraiment partir de ma feuille pour le raisonnement. J'ai déjà vu le développement par les aires des rectangles de la méthode de Viète. Moi je l'ai fait avec les triangles rectangle. Je vous poste la suivante:
en fait, je ne comprend pas bien ta question.
et ton approche est similaire à celle d'eudea, qui n'utilise pas les aires non plus mais bien les demi-angles à chaque itération.
On peut ajouter qu'il existe déjà un très grand nombre de formules de suites aboutissant à pi.
Dont beaucoup convergent bien plus vite.
Mais ton approche fonctionne si c'est ta question .?
Je vais compléter ce qu'a dit justement ansset.
Ta formule y(n)=f(y(n-1)) exprime directement la longueur du côté du polygone à m côtés en fonction uniquement de la longueur du côté du polygone à 2m côtés. Cette formule appelée formule de récurrence engendre la suite que tu connais.
Dans le calcul que j'ai développé, j'utilise la formule de récurrence suivante :
que géométriquement on peut écrire (avec tes notations) :
K étant le milieu de [AB].
Tu vois bien que cette formule de récurrence exprime la longueur du côté du polygone à m côtés en fonction non uniquement de la longueur du côté du polygone à 2m côtés, mais qu'il y a en plus la longueur OK. Cette formule engendre alors le produit infini de Viéte. Parce qu'à chaque étape ressort ce facteur.
Comment passer de l'un à l'autre, je ne vois (*) malheureusement pas d'autre alternative que de changer de formule de récurrence.
(*) ce n'est que mon avis !
Attendons alors l'avis d'autres artistes des mathématiques. ^^ Non, mais je crois que j'ai trouvé... je récupère le résultat de pi(-3) et je calcule pi(-2) et je divise le résultat de pi(-2) par pi(-3) et je trouve alors la multiplication suivante sous forme de chiffres et elle est bien égale à l' itération de la formule de Viète...Et vu que cela se répète, on peut l'écrire au final. ^^...Comment passer de l'un à l'autre, je ne vois (*) malheureusement pas d'autre alternative que de changer de formule de récurrence...(*) ce n'est que mon avis !
Bon, et bien, désolé pour le dérangement, cela s'est décoincé après avoir posté sur le forum...^^
En vous souhaitant une bonne soirée, et une bonne semaine à tous.
