J'ai une matrice Hermitien définie positive $P=P^*>0\in\mathbb{C}$, telle que $P*$ est transpose conjugué de $P$ et $r=\exp(i\theta)=. Alors, comment puis-je montrer que:
$$ (rP+\bar{r}\bar{P})^{-1}=rY+\bar{r}\bar{Y}$$
Tel que $Y$ est une matrice Hermitien définie positive et $\bar{Y}$ son conjugué?
Rappel de la charte du forum :
Et merci d'utiliser la fonction de prévisualisation de vos messages et la balise TeX correcte.2. La courtoisie est de rigueur sur ce forum : pour une demande de renseignements bonjour et merci devraient être des automatismes.
Not only is it not right, it's not even wrong!
Vraiment désolé pour la male écriture j'ai oublié comment ecrire en latex j'ai cru que les dollars jouerons le role. Merci de me donner l'autorisation de modifier mon msg.
cordialement,
on ne peut pas revenir sur un message déjà posté, éventuellement demander à le supprimer.
par ailleurs la balise Latex ( en mode avancé ) n'est pas lisible.
c'est l'avant dernière dans le bandeau le plus bas qui apparait en blanc.
donc j'essaye de le faire pour toi, en espérant avoir bien recopié ton énoncé.
J'ai une matrice Hermitienne définie positive:
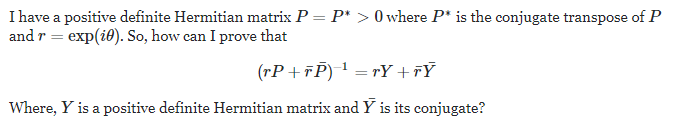
, telle que
Alors, comment puis-je montrer que:
Tel que
Ou demander à un modérateur de le faire. Je ne me permet de modifier les messages sans l'autorisation de l'auteur que s'il y a des infractions à la charte.Envoyé par ansset
Là, j'arrive trop tard, vous avez retranscrit l'énoncé.
Not only is it not right, it's not even wrong!
désolé !
cordialement.
bjr
Je crois qu'on peut exprimer Y en fonction de P.
Après il faut démontrer que Y a les propriétés demandées.
Voici une première ébauche, en espérant qu'il n'y ait pas d'erreurs:
hermitia.pdf
Merci a tous le monde. Et pour pilum2019 vous avez fait un bon travail.
