Bonjour,
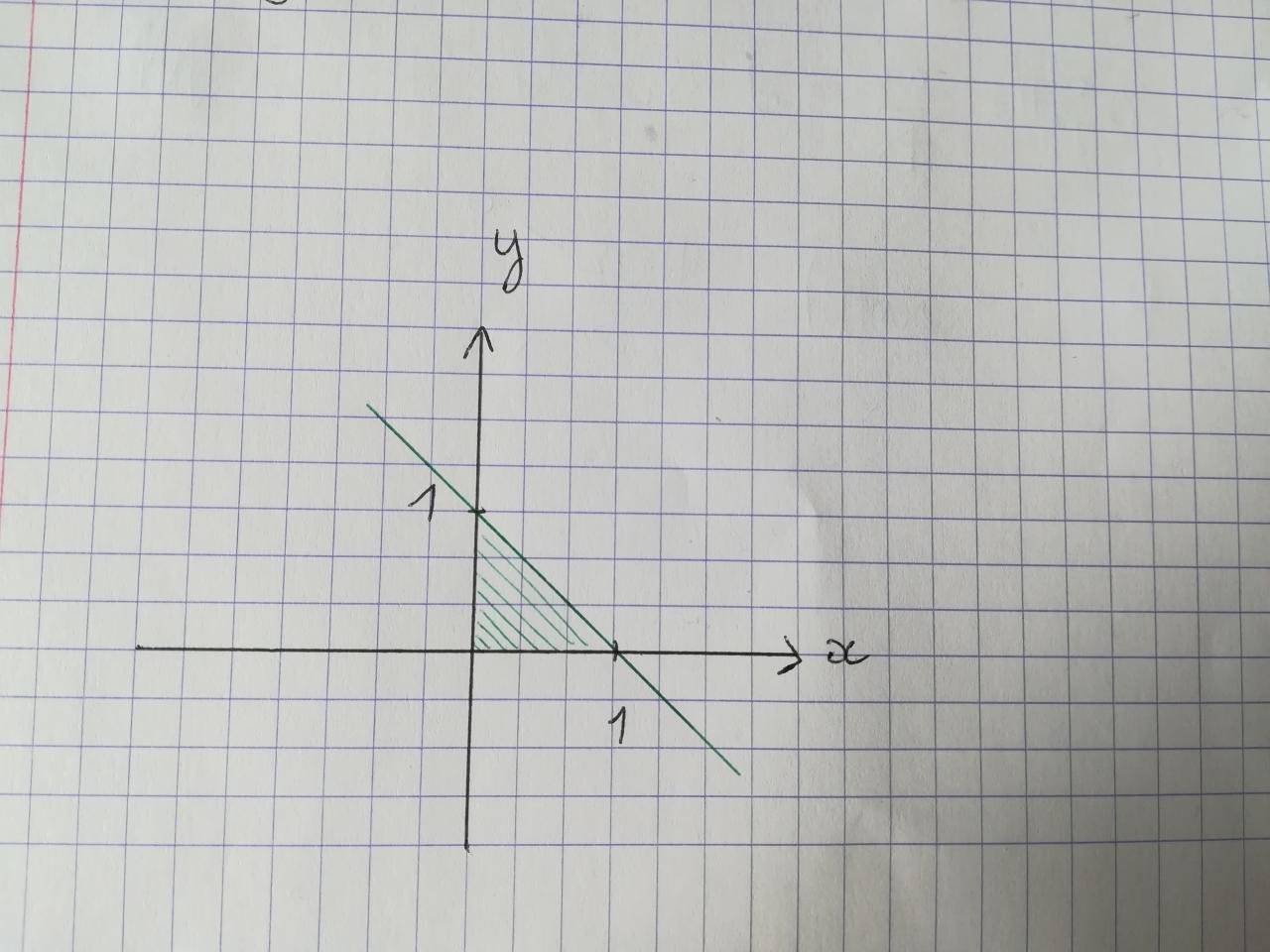
Dans un exercice je souhaite calculer une intégrale double qui dépend de 2 varibles : x et y.
Dans l'exercice, x varie de 0 à 1 et y varie de 0 à 1-x.
Je réalise le changement de variable suivant : u=y-x et v=y+x.
Ainsi, je calcule le jacobien qui vaut 2 en valeur absolue. Cependant, je rencontre un problème lors du changement de variable : je n'arrive pas à savoir dans quel intervalle varient u et v.
Merci d'avance,
Faire un dessin est utile.
On peut alors voir queet
Merci pour votre réponse mais pouvez vous m'expliquer comment vous faites svp?
Il l'a dit :
L'avez-vous fait au moins ?Envoyé par Tryss2
Not only is it not right, it's not even wrong!
Oui j'ai réalisé le dessin,
J'arrive à comprendre avec la notion de minimum et maximum que v varie entre 0 et 1 mais j'ai du mal à encadrer u.
Est-ce que tu peux tracer les lignes u= constante, et donner l'ensemble des valeurs que peut prendre v sur cette ligne ?
Bonjour non je n'y arrive pas car je n'arrive pas à visualiser le repère de (u, v) donc je ne sais pas dans quelle orientation tracer u=cste
Quand même...
Je l'ai déjà fait et représenté mais je ne vois pas où vous voulez en venir... je ne trouve pas
autre présentation:
u=y-x
v=y+x
u+v=2y => 0<=u+v<=2 et u+v=0 correspond à x=1 y=0
donc -v<=u et borne atteinte
de même
u-v=-2x => -2<=u-v<=0 et u-v=0 correspond à x=0 y=1
donc u<=v et borne atteinte.
Bonjour,
Tout d'abord merci beaucoup pour toutes les réponses.
Finalement j'ai trouvé une méthode beaucoup plus visuelle : mon domaine dans (x,y) est un triangle (Colorié en vert sur mon schéma)
Je prends mes 3 sommets du triangle en coordonnées (x,y) puis je les exprime aussi dans le repère (u,v) grâce aux relations u=y-x et v=y+x
Puis on voit très bien l'intervalle sur lequel est compris u
bonne journée
