Bonjour,
J'ai trouvé ce que je cherchai avec mon histoire de "carré de Mondrian" cf post en science amusante.
En étudiant la suite formée par l'intervalle de nombres premiers de 137 à 193 (137,139,149,151,157,163,167,1 73,179,181,191,193) j'ai constaté que la somme des termes était constante en aditionnant le premier avec le dernier, le deuxième avec l'avant dernier etc.. soit une valeur de 330.
137+193=139+191=149+181=151+17 9=157+173=163+167=330
J'ai en cherché ce genre de relation à l'intérieur des suites formées par les résidus de la division euclidienne pour ces nombres et j'ai trouvé pour mod(120) (pour faire le triple égal je vais noté /// )
137///17mod(120) ,139///19mod(120) etc.. soit la suite suivante de restes (17,19,29,37,43,47,53,59,61,71 ,73) la constante des sommes obtenues par la méthode des sommes des opposés décrites plus haut est 90:
17+73=19+71 etc..=90
Partant de là l’extension est simple, la somme des deux termes opposés dans la suite de nombres premiers est égal à 330 et ceux de la suite de restes à 90, je cherche le reste r inférieur à 19 tel que r+120 soit premier et 330-(r+120) le soit aussi et j'arrive à étendre ma suite "carré de Mondrian" en décroissance et en croissance.
Peut-on dire que le fait de connaître deux "petits" nombres premiers p1 et p2 tel que p1+p2=120 permet de connaître deux plus "grands" avec cette relation?
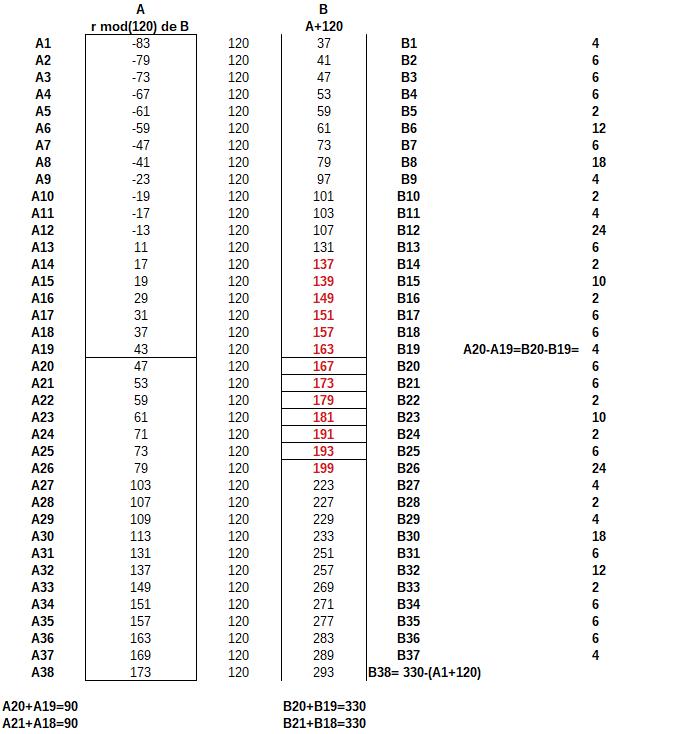
Je vous propose un tableau pour illustrer mon propos:
Pièce jointe 398602
-----