Bonjour,
J'ai une matrice et je dois démontrer qu'elle est diagonalisable, j'aimerai la simplifier avant de procéder aux nombreux calcules mais je ne sais pas si j'ai le droit de faire ces nombreuses opérations (voir pièce jointe). Pourriez vous m'aider s'il vous plaît en disant si c'est juste ou non. J'aurais également aimé savoir quand est ce qu'il est judicieux de calculer l'exponentielle d'une matrice? Merci d'avance
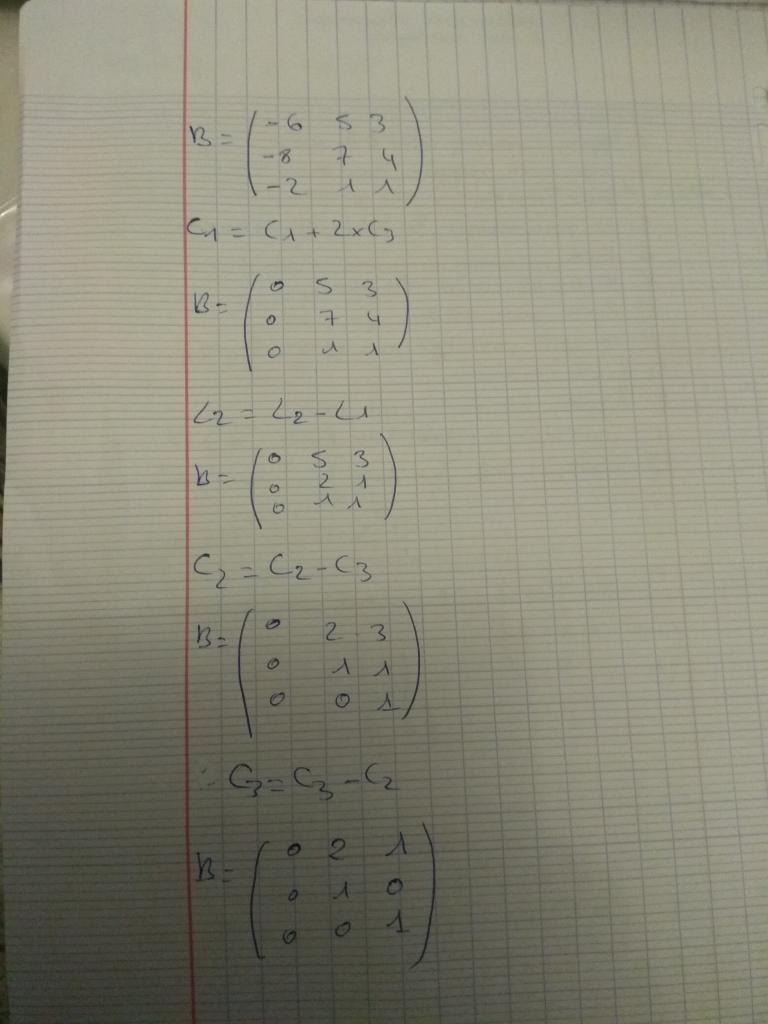
Bonjour,
Tu as donc triangularisé ta matrice.
Ses valeurs propres, situées sur sa diagonale, sont donc 0 de multiplicité algébrique 1 et 1 de multiplicité algébrique 2.
Pour répondre à la question, il te faut déterminer la dimension du sous-espace propre associé à la valeur propre 1 ...
salut,
en général, tu ne peux pas commencer par échelonner puis regarder les valeurs sur la diagonale pour avoir les valeurs propres ( en échelonnant, on verra seulement si 0 est vp ou non); on peut toujours échelonner une matrice, alors que sur R, il existe des matrices sans valeurs propres ( dans le plan, une matrice d une rotation d un quart de tour par exemple, de pol. cara. X²+1 ).
Dernière modification par slivoc ; 12/01/2020 à 08h50.
