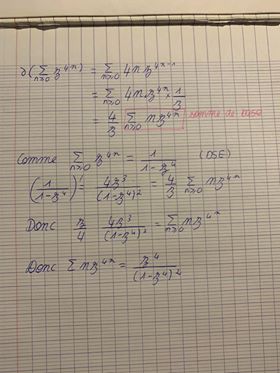Somme de série entière

[lolette99]

Bonjour,
Voici l'exercice que j'ai à faire dans le cadre d'un DM qui porte sur les séries entières :



J'ai réussi à calculer la rayon de convergence de la série grâce au critère des séries numériques de D'Alembert. J'ai fais Un+1/Un et j'ai trouvé un rayon de convergence égal à 1.
Pour la question de la somme de la série, je ne comprends pas vraiment en quoi la somme écrite en-dessous peut aider à calculer la somme de la série que nous devons calculer. Je l'ai quand même calculée et j'ai trouvé qu'elle était égale à 1/(1-z^4).
J'ai essayé de dériver la somme écrite en aide pour trouver une correspondance avec celle que nous devons calculer mais cela n'a abouti à rien.

Bonne journée
-----

[jacknicklaus]

indice : calculer la dérivée de la fonction sur R définie par



où n est un entier positif.

[lolette99]

Cela me donne f'(z)=4n*z^(4n-1)
Cela ressemble à la somme que nous devons calculer mais le puissance n-1 me gene

[gg0]

mot clef : factorisation.

[A voir en vidéo sur Futura]

[lolette99]

factorisation de la dérivée ?

[gg0]

On factorise dans une somme, non ?

[lolette99]

si je factorise par 4 la dérivée de la somme (z^(4n)), cela me donne 4(somme(n*z^(4n-1))
cela ressemble à la fonction de départ à part la puissance 4n-1

[jacknicklaus]

indice :

[lolette99]

J'ai trouvé quelque chose avec l'indice que vous m'avez donné. voila ce que j'ai fais :
ce n'est pas très bien rédigé, merci pour votre aide
je ne suis pas certaine que ce soit correct