vitesse d'un point sur une sphère en expansion

[doslegartos]

Bonjour à tous,

J'aimerais trouver la vitesse d'un point sur une sphère qui enfle uniformément. A ce sujet j'ai plusieurs questions. Mais d'abord je vais montrer où je me suis perdu. J'ai beaucoup à apprendre, j'espère être compréhensible.

1. La sphère étant en expansion, le volume augmente, le point qui appartient à la sphère s'éloigne donc du centre.

Ne sachant par où prendre le problème et que je sais comment calculer le volume d'une sphère j'ai voulu visualiser l'effet dans un tableur les valeurs que prenaient :

- V selon r = ((3.V)/(4π))^(1/3)
- r selon V = (4π.r³)/3

J'ai pas été choqué de voir des fonctions exponentielles mais ça m'avance peu. Alors j'ai dessiné*:



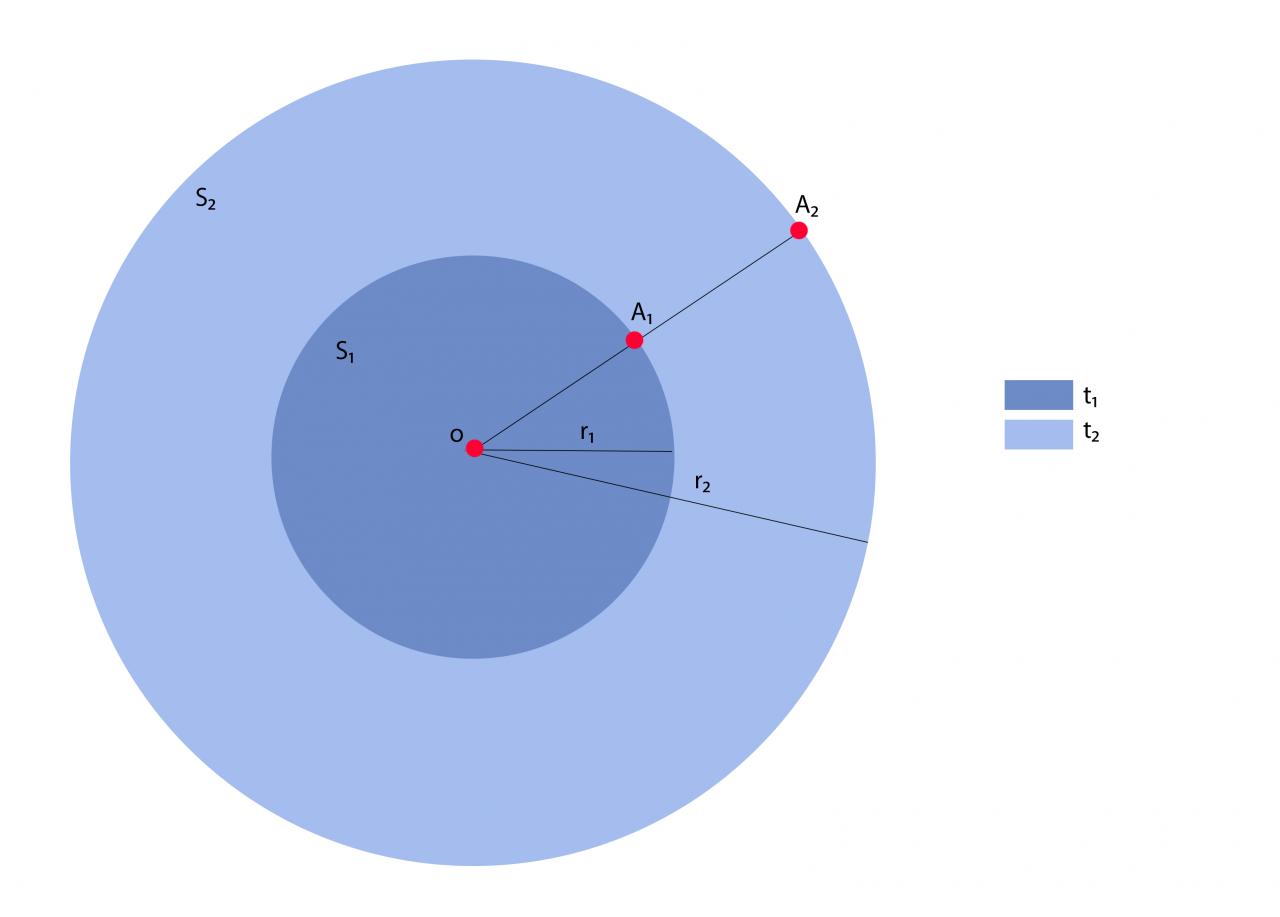
Soit une sphère dynamique S de centre O prise à deux intervalles de temps t1 et t2. On appellera S1 l'instantané de la sphère de volume V1 et de rayon r 1 et du centre O, prise à l'instant t1. Et S2 l'instantané de la sphère à un instant t2, de même centre O et de volume V2 et d'un rayon r2. On appellera A un point sur la Sphère appelé A1 à l'instant t1 et A2 à l'instant t2. Quelle est la vitesse Va du point A*entre t1 et t2?

2. La vitesse est une distance parcourue en un temps donné. Donc la vitesse du point A vaut la différence entre la position de A au temps T2 moins sa position au temps t1 sur l'écart de temps mesuré (t2 - t1).

Va = (A2 – A1) / (t2 – t1)

Le point A appartenant à la sphère S de centre O, la distance [OA] est égale au rayon on a donc:

Va = ( r2 - r1 ) / ( t2 - t1 )

Je trouve ça trop incomplet. J'aimerais obtenir une valeur en fonction du volume; donc:

Va = ([((3.V2)/4π)^(1/3)] - [((3.V1)/4π)^(1/3)]) / ( t2 - t1 )

Ça fonctionne comme ça ou c'est faux?

3. Autre question facultative :

Alors je me demande si je peux utiliser les sphères de n dimensions et considérer ma sphère qui enfle comme une 3-sphère*? Le temps étant ma 4ème dimension finalement.

A ce moment il me suffirait d'utiliser les formules déjà définies et la valeur du rayon d'une 3-sphère. Avec n=4 (paire) dans mon cas de 3-sphère, le 3-volume serait*:

V = (π².r⁴)/2

Ce 3-rayon correspondrait à la vitesse de mon point dans la 2-sphère fonction du volume.

r = ((2.V)/(π²))^(1/4)

Je fais fausse route*si je fais ça*? Qu'est-ce qu'il faut que je bosse pour pouvoir résoudre ce problème? Une piste pour m'orienter sans me donner la solution dans un premier temps?

Merci d'avance à ceux qui m'aideront à embrasser ce problème.
-----

[ansset]

J'aimerais trouver la vitesse d'un point sur une sphère qui enfle uniformément.

même si elle enfle uniformément, il te faut préciser comment.
donc préciser une fonction du temps, soit pour le rayon, soit pour sa surface, soit pour son volume.
cette fonction du temps peut être linéaire ou pas, d'ailleurs.

sachant que dans tous les cas la vitesse de ton point sera la vitesse d'augmentation du rayon. ( que l'on peut déduire d'une fonction liée à la surface ou au volume si c'est le modèle choisi )

[doslegartos]

Comme par exemple f(t)=t.(x+V) pour un volume qui augmenterait d'un volume constant et f(t)=t.(x.V) pour un volume qui augmenterait d'un volume croissant?

Merci, je vais creuser ça demain, je reviendrai voir si j'ai su utiliser tes conseils.

[ansset]

Edit: je reformulerais demain.

[A voir en vidéo sur Futura]

[gg0]

Bonjour.

Comme la sphère est définie par son rayon, il suffit de connaître le lien entre le rayon et le temps : r=f(t).
par exemple r=t pour une croissance linéaire; r=t² pour une croissance quadratique; r=1 -1/(t+1) (t>=0) pour une croissance finie.

Le fait de calculer en fonction de V à la place de r ne change pas grand chose (en tout cas pas la vitesse), mais il faut une liaison entre la sphère et le temps. La vitesse est un rapport distance/temps, si la distance ne dépend pas du temps, ça n'a plus de sens.

Cordialement.

[ansset]

re-, et désolé ( j'ai du interrompre brutalement hier soir ).
comme je le disais il faut que tu précises la valeur qui augmente et de quelle manière.
sachant qu'au bout du compte la vitesse du point à la surface sera celle de son rayon.

ainsi , si tu proposes que le rayon évolue linéairement:
r(t)=kt+r0 alors la vitesse d'un point qcq sera bêtement r'(t)=k

si tu proposes que c'est le volume qui évolue ( je reprend un cas linéaire ), alors il faut faire un calcul pour en déduire l'accroissement du rayon.
on sait que
d'où

supposons une croissance linéaire du volume



Il faut donc maintenant trouver r'(t) et donc dériver cette expression.
ce qui donne

soit en simplifiant

avec

on voit dans ce cas , que si la vitesse reste tj >0 , elle tend pourtant vers 0 au fur et à mesure que le volume augmente.

[doslegartos]

Merci à tous pour vos réponses! Maintenant je vais essayer d'assimiler tout ça!

Vous êtes super!

Modérateur: On peut peut-être placer ma question dans "maths du lycée". Ma question sur la 3-sphère étant finalement hors-sujet.