Salut,
Moi aussi (si, si, je suis toujours cette discussion dont je suis heureux de voir qu'elle a fini par bien fonctionnerEnvoyé par minushabens
)
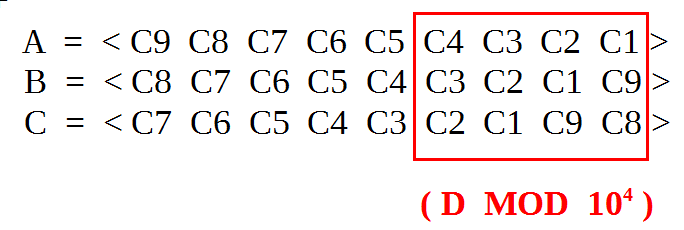
A moins de poser diverses contraintes limitant le nombre de solutions. Et c'est loin d'être évident. Il faut peut-être voir quelle est l'objectif : pourquoi ce problème des sommes de permutations ? Ca pourrait aider à trouver ces contraintes. Pour peu que cela ait un intérêt, je ne sais pas.
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Sous ce rapport, tu vas être déçu.Je suppose qu'en augmentant la longueur des nombres, le nombre de solutions tend vers 1.
Une erreur numérique stupide (ça l'est toujours) et très discrète compromettait le calcul final.
Fin de la liste de la présélection: 100 combinaisons ont été retenues sur les 106 possibles, soit une proportion de 1/10000 .
La durée d'exécution n'atteint une demi-seconde; je suis franchement surpris par cette rapidité.
Merci, c'est plus logique comme ça (je ne suis pas logique). Pourrais-tu tester le même D à 5 permutations STP ? Uniquement pour comparer. Pour ce qui est du zéro, je ne me suis pas trompé, je ne considère pas 0 comme chiffre isolé : 90318 / 31890 / 18903. Même non standard, cette combinaison existe et donc doit apparaître avec les autres. On a eu comme exemple 23001 et ça a marché (le standard donnerait : 23001 / 30012 / 00123).
J'ai dit une bêtise là. La raison à été donnée, j'étais distrait. Et là, l'augmentation des solutions, ça peut ne pas être une gêne, ça dépend des protocoles. Je laisse donc continuer
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Combinaison 3, pourquoi B et C prennent un zéro supplémentaire ?
On devrait avoir :
A : 62787120
B : 278712062
C : 787120622
Du coup, D est changé.
OK j'ai compris (!)
Quand même, pourquoi A démarre-t-il avec un zéro ?
[QUOTE]Quand même, pourquoi A démarre-t-il avec un zéro ? [/QUOTE
Parce que les 9 chiffres du premier entier recherché ont fait l'objet d'une énumération systématique, par une instruction du type:
Si tu tiens à supprimer les réponses à (c) chiffres commençant par un ou plusieurs zéros, tu peux imposer aux 3 entiers la condition:Code:FOR X[i]:=0 TO 9 DO ...
A (ou B ou C) >= 10(c - 1) .
Je le vois comme une transgression contre la logique implicite de l'énoncé, qui suppose que les chiffres successifs se décalent d'une position d'un entier à l'autre. En plus cette tolérance complique l'algorithme.Pour ce qui est du zéro, je ne me suis pas trompé, je ne considère pas 0 comme chiffre isolé : 90318 / 31890 / 18903. Même non standard, cette combinaison existe et donc doit apparaître avec les autres. On a eu comme exemple 23001 et ça a marché (le standard donnerait : 23001 / 30012 / 00123).
Mais tu fais évidemment ce que tu veux.
Oui, mais ton programme a visiblement fait une exception pour 23001. Compte tenu de la "transgression", il n'aurait pas dû afficher de résultat. Ces combinaisons non standard méritent d'être étudiées (puisqu'elles existent).
Ex (à 3 permutations): A = 320523269 / B = 205232693 / C = 523269320. Au lieu de calculer avec 9 chiffres, on calcule avec 8 (dont le nombre 20), tous les nombres ont le même nombre de chiffres et zéro sert à quelque chose (on n'a pas : 0319 , par exemple, dans lequel il ne sert à rien). Cette conception a quelque chose à voir avec la cryptographie (lettres chiffrées).
L'algo est plus compliqué certes (s'il est plus lent, c'est même mieux), mais la distribution de tels triplets est probablement très différente pour un D donné, à priori plus économique, du fait que A commence toujours par un nombre à 3 chiffres contenant un ou deux zéros.
On peut essayer sur des 5 et 6 chiffres pour commencer. Si tu estimes que c'est inutile, on s'arrête là.
Bonne soirée.
Je n'ai jamais envisagé ce cas, et le programme gère le zéro comme les 9 autres valeurs entières; dans le cas de séquences de longueur 5, les deux entiers successeurs de (A = 23001) s'obtiennent par les relations:... mais ton programme a visiblement fait une exception pour 23001
B = 10*(A MOD 104) + (A DIV 104) = 10*3001 + 2 = 30012 ;
C = 10*(B MOD 104) + (B DIV 104) = 10*12 + 3 = 123 .
Ce qui aurait dû être clairement dit, c'est que (B) et (C) sont des permutations circulaires de (A), ce qui implique de travailler sur des chaînes de caractères de longueur fixe.
Réduire "00123" à "123", c'est introduire le réflexe humain de lecture dans le codage et se condamner à un algorithme complexe, se prêtant peu à une démarche simplificatrice.
Il faudra, dans le cas d'un entier (A) à neuf chiffres, envisager une à une les 109 combinaisons possibles ... donc faire preuve de patience.
Dernière modification par Opabinia ; 08/06/2020 à 21h28.
@Opabinia : j'admire ta patience.
@akntn : et si tu te mettais à l'écriture d'un programme par tes propres moyens, au lieu de le faire faire par les autres et de critiquer leurs résultats ? Ne pas avoir produit la moindre ligne de code par toi même lors de ce fil, alors que tu t'intéresses à la cryptographie, me semble pour le moins surprenant, voire franchement antinomique.
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
Et c'est assez impoli de ne définir les contraintes que au fur et à mesure que les autres aident. Pourtant, dès le début, une demande de clarification des règles a été donnée, toujours sans réponse !!
Salut,
En fait c'est cette discussion qui est cryptée
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Opanibia, je comprends : ton programme est parti de A = 12300, donc pas de problème d'adaptation du zéro, le calcul est standard. Si on part de 30012 ou de 23001, le résultat est différent en standard. En non standard, je parviens au même résultat : 30012 / 12300 / 23001 (65313) et 23001 / 30012 / 12300 (65313).
Pour 90318, le programme ne peut pas trouver car le calcul standard donne un D différent de 141111.
Formes non standard avec 5 chiffres et 3 permutations
90000
90001 + 19000 = 109001
90010 + 10900 = 100910
90100 + 10090 = 100190
90012 + 12900 + 29001 = 131913
90123 + 12390 + 23901 = 126414
90102 + 10290 + 29010 = 129402
90120 + 12090 + 20901 = 123111
98000 + 80009 = 178009
98001 + 80019 + 19800 = 197820
98010 + 80109 + 10980 = 189099
98012 + 80129 + 12980 = 191121
Hypothèse : raréfaction
Voici ce que donne un programme zappant les zéros à gauche, en partant d'un entier à six chiffres, conduisant à une somme
D = 22455086 :
Les triplets anormaux sont aisément repérables.
Le prix à payer, c'est le recours à un algorithme néandertalien, plus simple mais dont le délai d'exécution est beaucoup plus grand (ici 121 s).
Je te laisse le soin d'estimer ce qui va se passer pour des nombres de 9 ou 10 chiffres ...
Dernière modification par Opabinia ; 10/06/2020 à 10h37.
Salut,
Et de plus le nombre de possibilités explose quand même, malgré le souhait.
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Dans les programmes précédents, la convention d'un décalage fixe des chiffres permettait une présélection très efficace, qui diminuait considérablement le nombre de calculs à effectuer; il suffisait pour cela de contrôler la valeur de la somme partielle sur un nombre réduit de chiffres (par ex. 4) comptés à partir de la droite:
On avait ainsi: D MOD 104 = 111*X[1] + 1110*X[2] + 1100X[3] + 1000X[4] + X[8] + 11*X[9] ,
dont le calcul était très rapidement effectué.
On aurait pu de même envisager d'autres décalages, par exemple de deux positions de (A) vers (B), puis de 3 pour aller au terme suivant.
Mais ce stratagème devient impossible dans le cas d'un décalage variable, dépendant du chiffre placé à l'extrême-gauche: il faut alors examiner le cas de tous les entiers (A) à (c) chiffres, variant par conséquent de (10(c - 1)) à (10c).
Voici le programme source rédigé en Pacal, qui se lit pratiquement comme du pseudo-code, et que tu traduiras sans peine dans ton langage préféré:
Instructions d'affichage:Code:PROGRAM XXX; // EnC = 1000000 121 s USES Crt, E_Texte; CONST NmaxT = 10000; Nd = 2245086; E1 = 10; EnC1 = 100000; EnC = E1 * EnC1; TYPE Quad_E = ARRAY[1..4] OF LongInt; Tab_Qe = ARRAY[1..NmaxT] OF Quad_E; VAR LstQ: Tab_Qe; PROCEDURE Aff_T(j: LongInt); CONST o = 13; BEGIN E(0009); We(5, 5 + j, j, 5); E(0014); Write(LstQ[j][1]:o); Write(LstQ[j][2]:o); Write(LstQ[j][3]:o); E(0012); Write(LstQ[j][4]:o); E(0013) END; FUNCTION Success(x: LongInt): LongInt; VAR u, v, w: LongInt; BEGIN u:= x; REPEAT v:= E1 * (u MOD EnC1); w:= u DIV EnC1; u:= v + w UNTIL (u>=EnC1); Result:= u END; PROCEDURE Enumeration(VAR L_q: Tab_Qe); VAR k, Na, Nb, Nc, s: LongInt; Nabcd: Quad_E; BEGIN k:= 0; FOR Na:= EnC1 TO (EnC - 1) DO BEGIN Nb:= Success(Na); Nc:= Success(Nb); s:= Na; Inc(s, Nb + Nc); We(60, 2, Na, 9); IF (s=Nd) THEN BEGIN Inc(k); Nabcd[1]:= Na; Nabcd[2]:= Nb; Nabcd[3]:= Nc; Nabcd[4]:= s; L_q[k]:= Nabcd; Aff_T(k) END END; A_ END; PROCEDURE Aff_0; CONST C1 = 5; L1 = 3; BEGIN E(1015); Wt(C1, L1 - 1, 'Somme D = '); Wt(30, L1 -1, 'Nombre de termes calcul‚s:'); E(0111); We(12, L1 - 1, Nd, 9); E(0015); Wt(C1, L1 + 1, 'k = '); Write('A = B = C = D ='); END; BEGIN Aff_0; Enumeration(LstQ); END.
Wt(x, y, '****'): écriture d'un texte ou d'un caractère;
We(x, y, k, n): écriture d'un entier sur (n) cases.
j'allais le dire, et j'avoue ne pas être surpris ( c'était purement intuitif ).
du coup, en tant que piste pour de la crypto, c'est pas vraiment une très bonne voie, si ?
ceci dit, même si c'est pas ma tasse de thé, il semble qu'il y en a deux qui s'amusent beaucoup avec cette histoire (*), et on ne peut leur reprocher.
(*) sachant que je n'ai tj pas compris les règles exactes !! je pense ne pas être le seul.
Ca dépend des protocoles. On ne sait pas du tout ce qu'il veut en faire. Il est même fréquent qu'une redondance soit utile.
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Opanibia : je constate que ton programme, pour D = 2245086, donne une seule forme non standard : 500079 / 795000 / 950007. La permutation 2 est standard et redonne le même D, sinon le programme n'aurait pas mentionné cette forme. Dans le cas de 90318 par ex, la permutation 3 (18903) est standard mais ne redonne pas le même D (141111), ce qui fait que le triplet 90318 / 31890 / 18903 n'est pas repérable, ou sinon par force brute (en testant tous les nombres). Il serait intéressant de savoir si, pour D = 2245086, il existe d'autres formes non standard que 500079 / 795000 / 950007 (en testant D par force brute). Mon idée repose justement sur l'impossibilité de détecter rapidement ces triplets non standard.
Merci pour l'ensemble de ces résultats.
Bon après-midi.
Il y a deux triplets anormaux, c'est a dire pour lesquels l'un des deux couples au moins (A, B) ou (B, C) ne vérifie pas la relation simple:je constate que ton programme, pour D = 2245086, donne une seule forme non standard : 500079 / 795000 / 950007.
Successeur(u):= 10 * (u MOD 100000) + (u DIV 100000) ;ce sont les triplets de rang (7) et (31), aisément repérables à la séquence de 3 zéros qu'ils comportent:
k=7 _ 500079 / 795000 / 950007On pourrait au passage leur associer celui de rang (22): k=22 795000 / 950007 / 500079 ,
k= 31 _ 950007 / 500079 / 795000
banal celui-là, et constitué des mêmes chiffres.
On observerait deux suppressions consécutives de zéros si l'on partait d'entiers tes que (905007) ou (900007) .
Le décalage simple des chiffres d'une position vers la gauche s'obtient par la fonction
(les instructions inutiles ont été maintenues à des fins de comparaison).Code:FUNCTION Success(x: LongInt): LongInt; VAR u, v, w: LongInt; BEGIN u:= x; v:= E1 * (u MOD EnC1); w:= u DIV EnC1; u:= v + w Result:= u END;
La suppression systématique des zéros à gauche découle de l'intervention de la boucle conditionnelle (REPEAT / UNTIL):
Il serait peut-être opportun de passer à la partie programmation, au lieu de discuter de cas particuliers (sujet certes inépuisable, mais un peu répétitif).Code:FUNCTION Success(x: LongInt): LongInt; VAR u, v, w: LongInt; BEGIN u:= x; REPEAT v:= E1 * (u MOD EnC1); w:= u DIV EnC1; u:= v + w UNTIL (u>=EnC1); Result:= u END;
Dernière modification par Opabinia ; 11/06/2020 à 15h19.
Tu ne nous as encore rien dit de la façon dont tu comptes utiliser les séquences (A, B, C, D) pour élaborer un procédé cryptographique.
Il serait intéressant de connaître des informations précises sur ce que tu recherches ...... C'est par rapport à un projet cryptographique que je pose ces questions ...
Le recours au binaire, la manipulation de bits ne fourniraient-ils pas des solutions plus simples ?
Bonjour, je comptais un seul triplet vu qu'on a les mêmes permutations. Je reviens sur mon projet.
Mon système est une variante minimaliste du système d'échange de clé de Ralph Merkle (très peu coûteux en opérations, aucune puissance ni multiplication, que des additions). Au lieu d'une liste de 2^32 problèmes, une liste de 10000 nombres seulement, ce qui n'empêche pas Eve d'avoir une chance sur 100 millions de trouver la clé.
Avant d'entrer dans les détails de l'algo, je dois :
1) Etre certain que les triplets non standard sont peu nombreux.
2) Connaître le temps de résolution du programme pour un D de 9 chiffres (celui-ci doit approcher les 10 ').
Salut,
J'ai une question bêtement terre-à-terre : pourquoi la recherche d'un protocole cryptographique (c'est pas ce qui manque et il y en a de super bon, super rapide...) ?
Actuellement la recherche tourne beaucoup autour de la cryptographie homomorphe (particulièrement utile et j'ai vu qu'il y avait déjà des applications) et la cryptographie post-quantique (crypto classique résistant au futur calcul quantique, y a divers tests et concours en cours).
Est-ce que c'est dans ces cadres là ? (aucune obligation de répondre, si tu préfères protéger tes travaux, c'est juste de la curiosité)
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Bonjour, je sais qu'il y a tout ce qu'il faut dans ce domaine (RSA). En l'occurrence, l'enjeu est d'utiliser un matériel extrêmement économique (fonction à sens unique basée sur 3 additions ...). La crypto homomorphe, je connais pas bien. La crypto post-quantique est intéressante, mais peut-on faire mieux que le masque jetable ? Une autre application de mon algo non standard est de pouvoir chiffrer un message (ou un texte) par lui-même (c'est à dire sans clé, et sans avoir recours à d'énormes nombres premiers) de telle manière qu'il soit seulement déchiffrable par l'ordinateur quantique. Absurde ? Peut-être pas, d'autant plus que cette machine est encore loin d'être opérationnelle. Mais ce questionnement n'est valable que si j'ai la certitude que mon algo repose bien sur une fonction unique.
Ce n'est pas avec des essais sur quelques cas particuliers que tu prouveras que tu as bien une "fonction unique". Pour des nombres faibles (comme ceux que tu as utilisés), un algorithme optimisé donnera directement le résultat voire tous les résultats (le plus long est le temps d'affichage). Et pour des nombres ayant suffisamment de chiffres pour ne pas être décodés rapidement, il faut une preuve. As-tu plus qu'une envie que ça marche ?
Cordialement.
Bonjour, je n'ai aucune preuve évidemment. Je compte sur la recherche d'Opanibia pour des nombres atteignant 9 ou 10 chiffres. Si 1) les triplets non standard sont uniques ou rares, et si 2) le temps d'exécution du programme est non polynomial, c'est "gagné".
