Bonjour à tous,
J'espère être au bon endroit pour ce genre de question
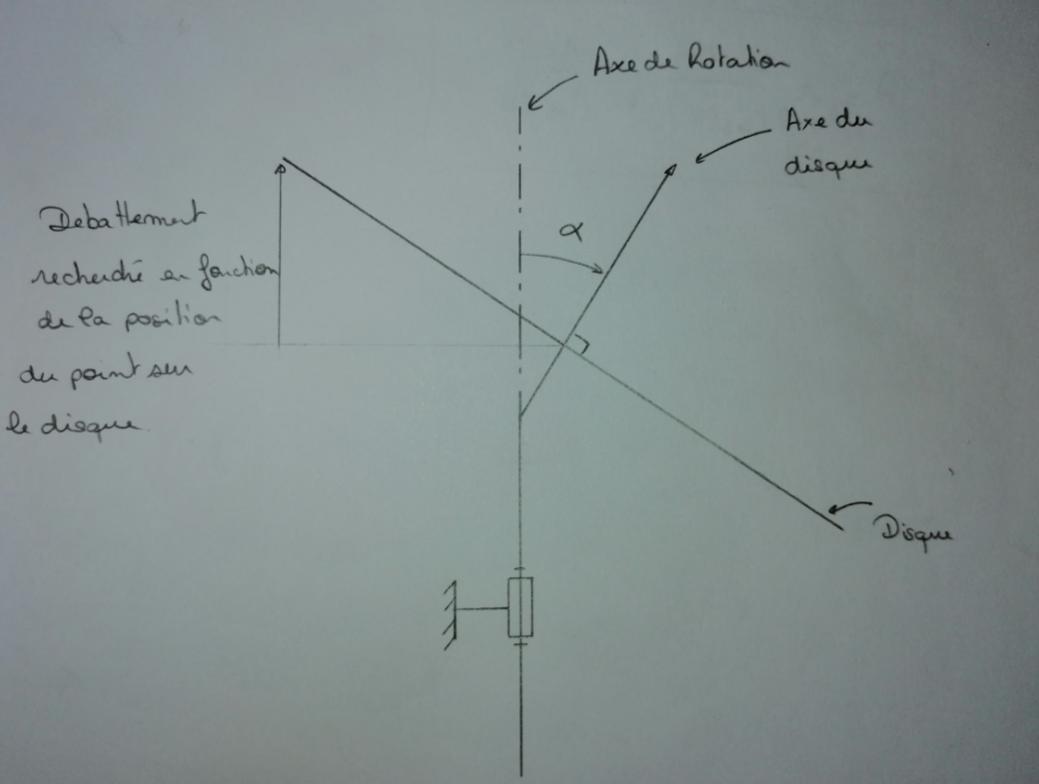
Je cherche à modéliser pour une future étude mécanique le battement radial d'un disque qui tourne autour d'un axe incliné en fonction de la position du point sur le plateau.
Je ne sais pas si c'est très clair.
Bonne journée à tous.
Bonjour,
tu parles d'un disque d'Euler ?
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
Oui ça pourrait y ressembler, je vous mets un schéma probablement plus clair ;p
Et dans un premier temps je peux considérer que les deux axes sont concourants au niveau du disque, ce qui enlève le battement radial si je ne m'abuse.
Salut
Quel battement ?
Tous les points décrivent un cercle .
Bonjour.
Sur le dessin du message #3 ce qui est marqué "débattement" vaut de façon évidente (trigonométrie élémentaire) R sin(alpha).
Cordialement.
Oui j'y avais pensé, mais je cherchais plus une manière d'obtenir le battement pour tous les points du plan lorsque le disque tourne.
Intuitivement ça devrait être un truc du genre h(r,theta)= r sin(alpha)*sin(theta+déphasage ) mais je ne vois pas trop comment l'obtenir proprement.
En tout cas merci de ton temps.
Et je m'attendais à trouver une équation de plan mais je ne suis pas sûr que c'en est une, (peut-être en coordonnée cylindrique) mais je ne vois pas comment le vérifier.
OK.
Mais un peu d'explication de ce que tu voulais et des données que tu as aurait été bien !
Tu peux considérer d'abord la question d'un disque fixe (tes points passent par différentes positions, mais comme tu présente ton problème, tu as laissé tomber le temps, donc le mouvement). Pour un point M, tu peux déterminer l'angle bêta de OM (O est le centre du cercle) avec le plan horizontal, puis en déduire par le même procédé, ton débattement : r sin(bêta). En utilisant un repère adapté de centre O, ça ne devrait pas être bien difficile.
Bon travail !
Rappel : imaginer la réponse est généralement inefficace en maths. Mettre en place les outils (noms, variables, méthodes) pour traiter le problème amènera à la vraie réponse.
Merci Beaucoup je vais essayer de refaire tout ça au propre.
Bonne continuation.
