Bonjour
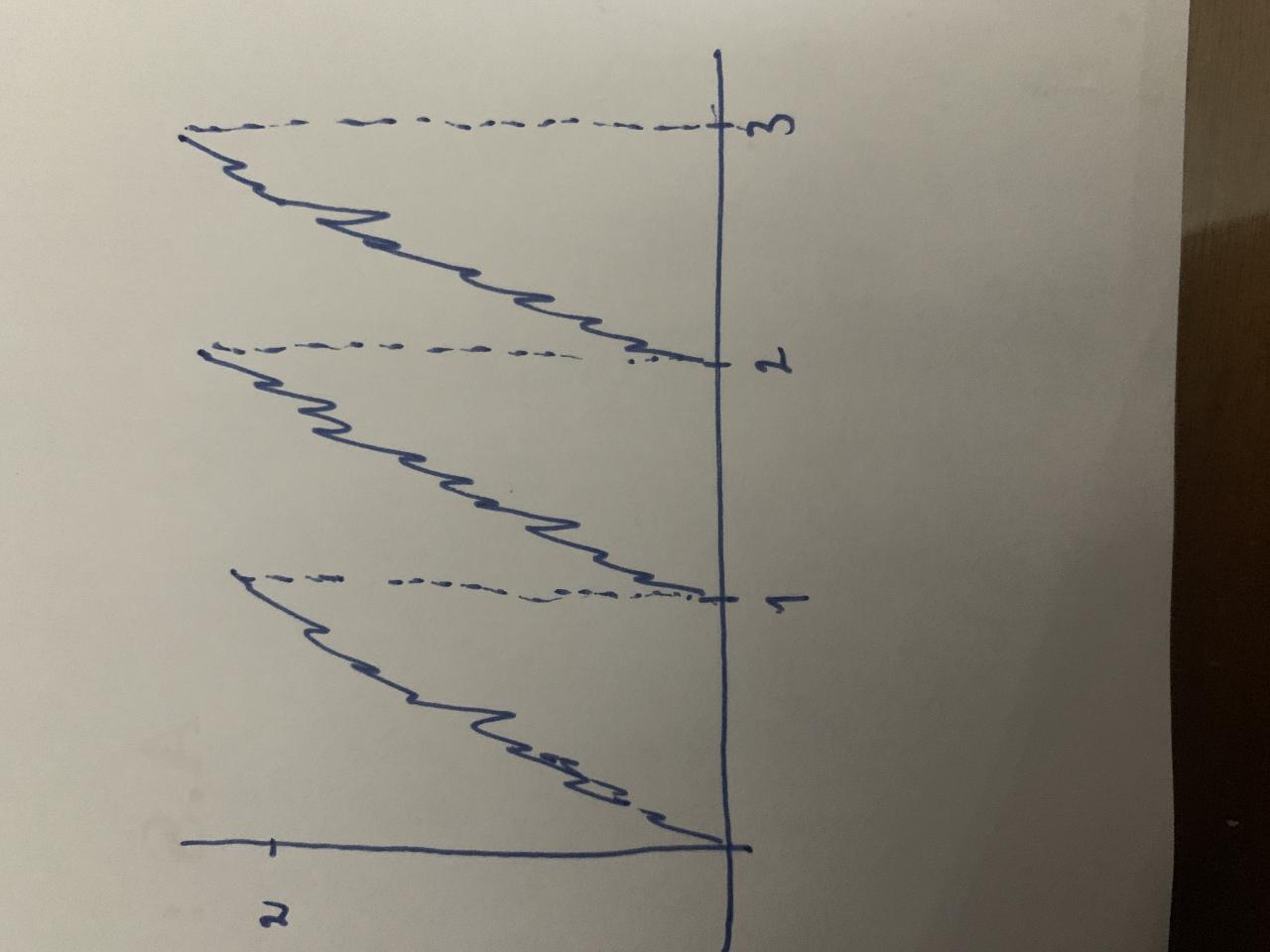
Pouvez vous m’aider à montrer que la fonction g est dérivable à gauche en tout point mais pas dérivable à droite en aucun point
Étant donné que la fonction fait intervenir la partie entière, j’ai pensé qu’un encadrement puis le théorème des gendarmes est le moyen à utiliser pour calculer la limite du taux d’accroissement
Ma recherche ainsi que la fonction sont en pièce jointe
Merci pour votre aide
-----



 et tout k, on a
et tout k, on a