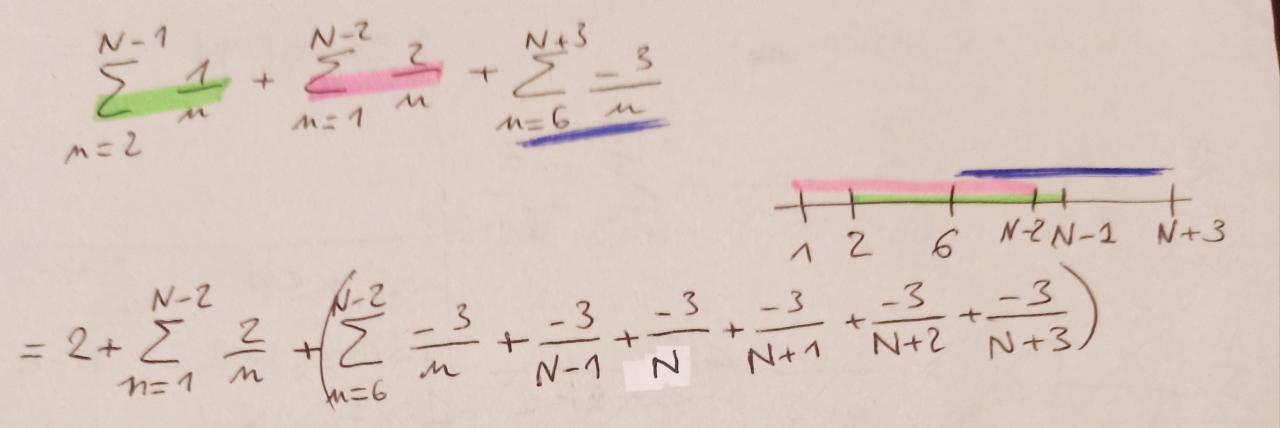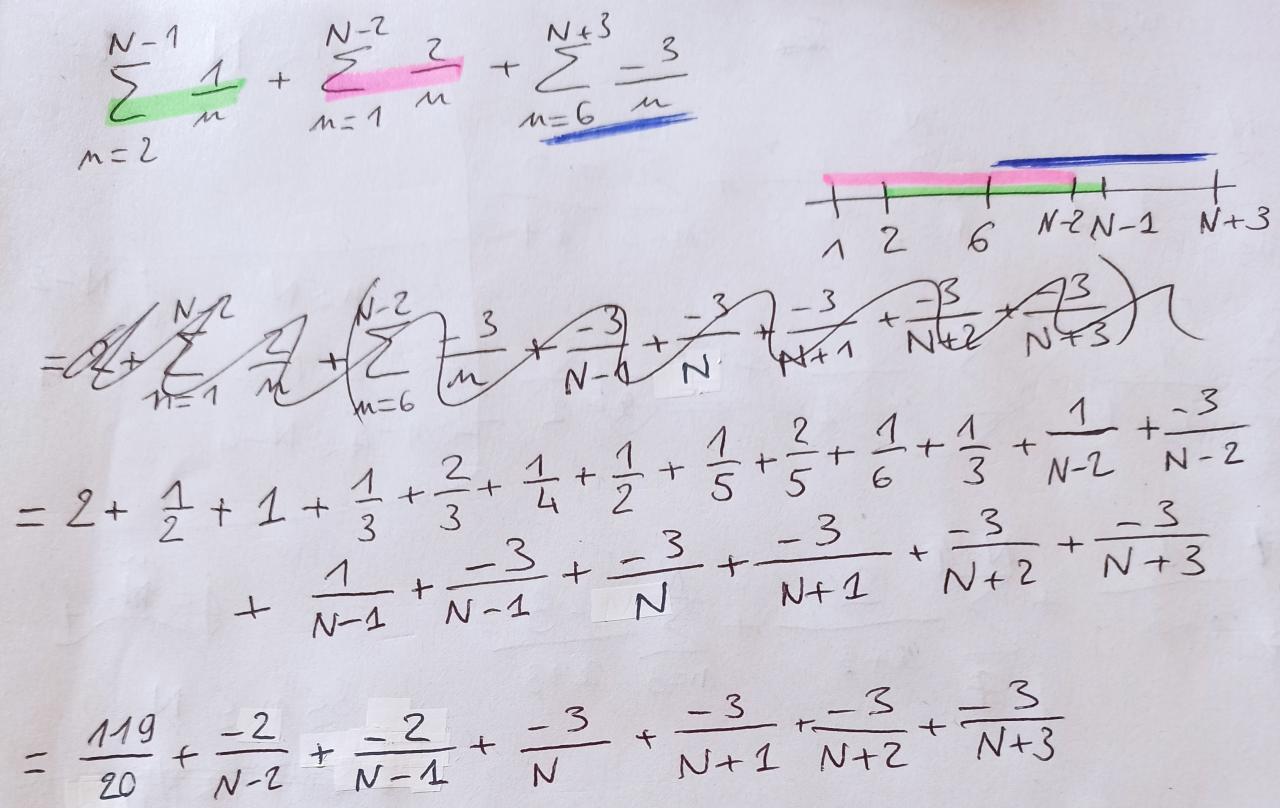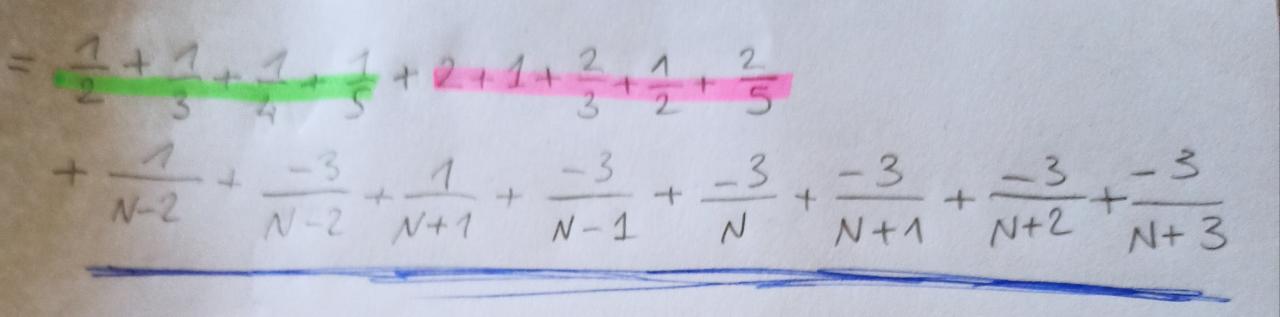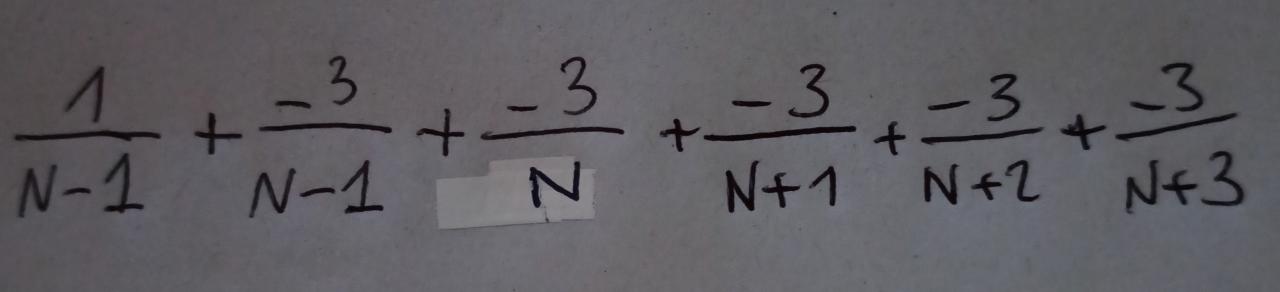Bonsoir,
J'ai un exercice à faire que voici :
Ce que j'ai fait :
1) J'ai cherché la limite du terme général de la série, j'ai trouvé que sa limite = 1. Comme 1 ≠ 0, la série diverge.
2) J'ai mis au même dénominateur puis par identification j'ai trouvé un système linéaire à 3 équations que j'ai résolu. Je trouve a = 1, b = 2 et c = 3.
À partir d'ici je bloque, je ne vois pas les termes qui se compensent donc comment calculer la somme de n = 3 jusqu'à N...
Pourriez-vous me guider ?
Merci d'avance,
Bonne soirée
-----





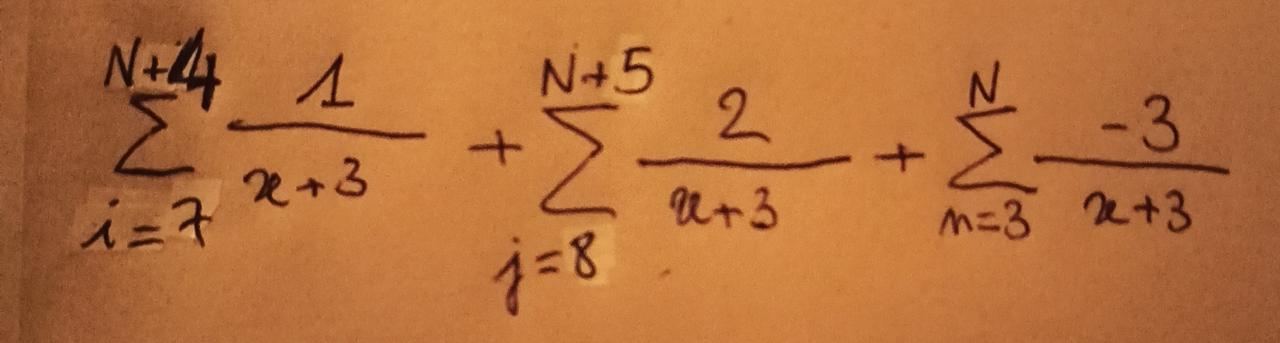
 ' et
' et