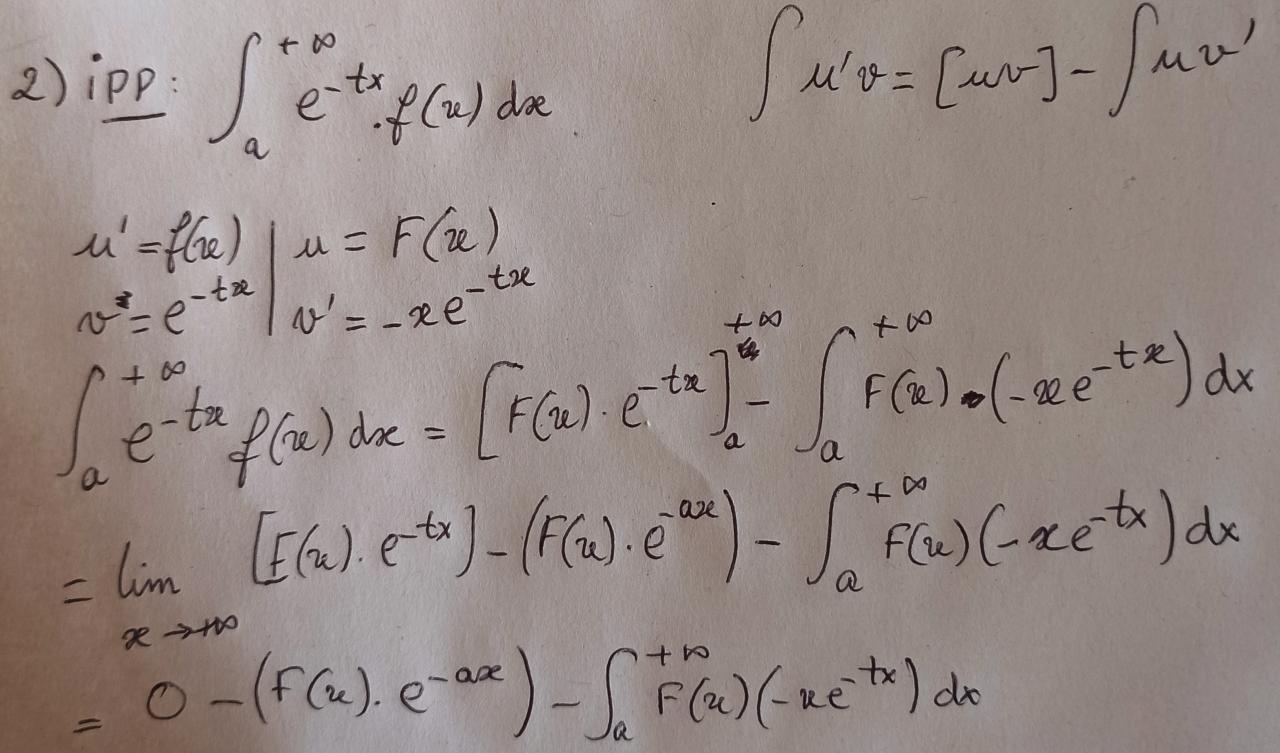Bonjour,
J'ai un exercice à faire dont voici l'énoncé :
1634289314899.jpg
J'ai fait les deux questions, j'aimerais savoir si ce que j'avais fait était juste.
1) Pour définir la convergence de l'intégrale, j'ai utilisé le théorème d'Abel. J'ai donc vérifié les conditions du théorème : f(x) est continue sur [a,+infini[ tel que l'intégrale de a à +infini de f(x)dx converge. Puis pour exp(-tx) : lim exp(-tx) = 0 en +infini, la dérivée de exp(-tx) = -xexp(-tx) comme elle est toujours négative la fonction est strictement décroissante, et exp(-tx) > 0 sur R donc elle est positive, elle est aussi dérivable et continue sur [a,+infini[. Donc d'après le théorème d'Abel, l'intégrale g(t) converge.
2) Voici ce que j'ai fait : 1634293230403.jpg
-----