Formule de Green-Riemann (pour le calcul d'aire)

[Scorp]

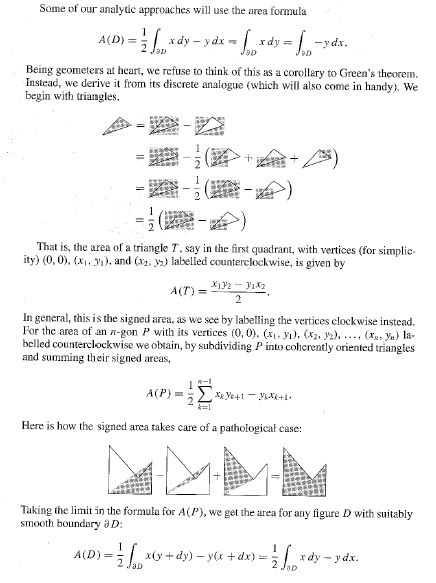
Bonjour à tous !
Je voulais démontrer les formules pour le calcul d'une surface :
Je suis arriver à la conclusion qu'il suffisait d'utiliser la formule de Green-Riemann :
en prenant Q=x et P=0
Mon problème est que maintenant, je n'arrive pas à montrer cette formule de Green-Riemann, surtout qu'à priori, cette formule doit marcher pour tout P et Q continues et tant que sont (à moins que je me trompe dans les hypothèses de ce théorème). J'ai essayé de la montrer en prenant et de montrer que mais sans résultats ( n'est pas forcément exacte, ni même fermée sinon serait toujours nulle, non ?)
Enfin bref, je nage un peu dans un flou magistral quand il s'agit d'intégrale curviligne et de différentielle, donc si quelqu'un pouvait m'aider à y voir plus claire...
Merci d'avance
-----

[GrisBleu]

Salut

Une idee simple est
- tu prend un rectangle (S) dont les frontieres sont paralleles aux axes x,y. La frontiere () est donc facile a parametrer. Tu calcule
facilement.
en gros, si les cotes sont (x=a,y=c), (b,c), (b,d) et (a,d), tu obtiens une expression, par exemple pour Q,

De meme pour P

- soit une surface pas trop tarte, tu peux, a la limite, la recouvrir de rectangle colles les uns aux autres (dont l'aire devient de plus en plus petite). Ce qu il faut verifier c est que tous tes rectangles soient orinetes de la meme maniere. Alors les contributions des cotes communs s annulent.

- la formule etant vraie sur la reunions des rectangles, a la limite, elle est vraie sur ta surface quelcconque, moyennant une surface suffisamment reguliere.

As tu compris l idee ?

++

[invite6b1e2c2e]

Salut,

D'ailleurs il y a la même idée pour démontrer la formule de Cauchy pour des fonctions holomorphes sur des lacets continus dans le Rudin, Real and Complex Analysis. (C'est juste avant que ça devienne vraiment complexe , au chapitre 10 je crois, enfin sur l'édition sur laquelle je travaillais)

__
rvz

[Scorp]

Il me semble que j'avais fait une démonstration un peu similaire pour montrer le théorème de Green-Ostrodasky et celui de Stokes-Ampère (mais c'était en physique). Donc j'espèrais qu'il y avait en math une démonstration sans passer par cette astuce de "maillage" de la surface.

[A voir en vidéo sur Futura]

[GrisBleu]

Si tu veux une vraie demonstration, il te faut le theoreme general.
Soit une forme n-1 lineaire sur une variete a bord, avec w differentiable (C1 ?) alors

regarde la par exemple
http://faculty.luther.edu/~macdonal/Stokes.pdf
tu verras que l histoire du maillage est encore utilise

++

[edpiste]

Une explication géométrique de l'intérêt du maillage (tirée d'un article de Blasjo sur l'inégalité isopérimétrique) :

[Scorp]

Tient, c'est sympa de faire remonter les anciens postes a la surface. Je vais allez voir ca de suite en espérant que ca soit pas trop dur pour moi : je ne suis même pas sur de savoir ce qu'esl l'inégalité isopérimétrique (c'est pas avec ca qu'on montre que pour un périmètre fixé L, la surface d'air maximal est le disque de périmètre L [ou quelque chose comme ca ])

[edpiste]

C'est exactement ça. L'article en question donne une bonne dizaine de preuves différentes de ce résultat, un peu à la manière du théorème fondamental de l'algèbre...