Equation distance entre droite et cercle

[inviteafb8ed29]

Bonjour à tous,

Mes meilleurs voeux pour cette nouvelle année,

Je bute sur un sujet au travail et je n'arrive pas à mettre la main sur la solution...



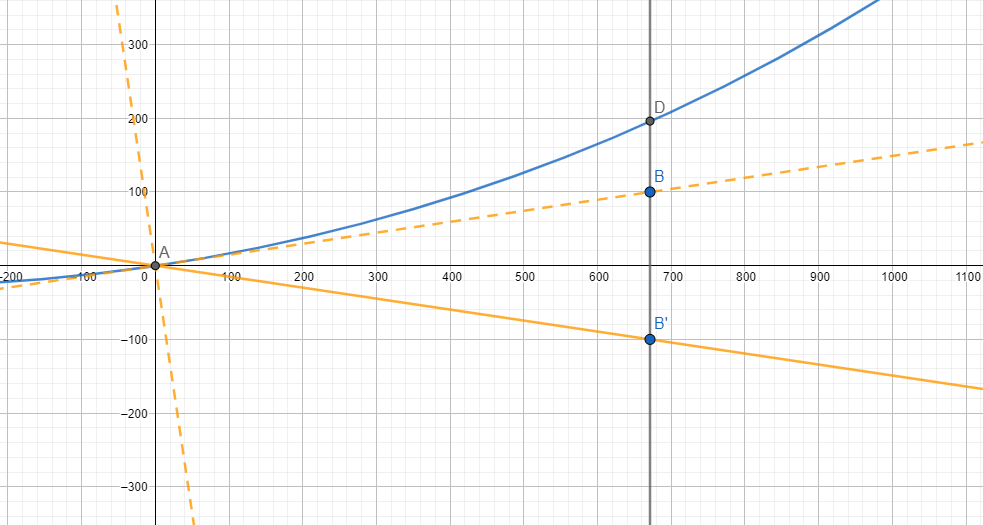
Sur l'image ci dessus ce trouve une droite (AB') avec A étant l'origine. la droite (AB) est la symétrie de la droite (AB) / X
Je connais l'angle B'AB donc je sais également définir l'equation de la droite (AB')

S'y trouve également un Cercle passant par A et tangent à la droite (AB) dont je connais également le Rayon R
J'arrive à trouver l'equation du cercle en faisant de la trigonométrie pour trouver son centre etc

Le point D est l'intersection, une des intersections qui m'intéresse, entre la droite (BB') ou (BD) qui est perpendiculaire à l'axe X, et mon cercle, ou arc de cercle.

Comment puis je connaitre la position en X de la droite (BD) pour une longueur de segment [B'D] donné ?

Merci pour votre aide !
-----

[gg0]

Bonjour.

Tu as l'équation du cercle, l'équation de la droite AB, donc tu peux trouver, pour une abscisse X0 de B l'ordonnée a de D, l'ordonnée b de B, donc la distance d=B'D = a+b en fonction de X0. Puis tu résous l'équation obtenue.
Si tu as du mal à résoudre l'équation, on t'aidera.

Cordialement.

[Polyalg]

Bonjour,
La tangente étant la perpendiculaire au rayon du cercle, faire une rotation de -90° dans le sens trigo.
Puis, par itération progressive, faire un petit déplacement pour obtenir un triangle. Puis, vérifier à chaque fois si le point B' coïncide avec D en testant si le point se trouve sur le rayon du cercle.
Il est sur le rayon, si R- racine ( (dx-cx) ² + (dy-cy) ²) = 0
cx et cy sont les coordonnées du centre du cercle.