Noyau / espace nul

[herrmattoon]

Ce fil a été extrait de la discussion de départ qui se trouve ici : https://forums.futura-sciences.com/m...-matrices.html afin de ne pas polluer le fil initial et d'ajouter de la confusion non nécessaire. Et aussi de poursuivre la discussion engagée ici.


Je suis attristé de lire une telle réaction . Je vais essayer - avec mon faible vocabulaire mathématique - d'illustrer mes propos :

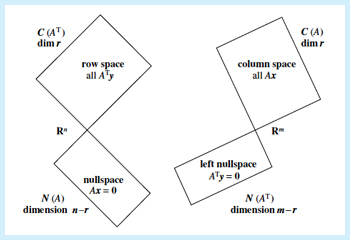
On peut représenter la multiplication d'une matrice avec un vecteur comme la combinaison linéaire des vecteurs colonnes de la matrice (première colonne * premier élément du vecteur,...,dernière colonne de la matrice * dernier élément du vecteur. C'est-à-dire :


La même chose se produit si l'on multiplie à gauche par le vecteur transposé, à la différence que le vecteur résultant sera la combinaison linéaire des lignes de la matrice, selon les éléments du vecteur.

Exemple avec une matrice de rang 2 (me suis pas foulé la rate disons que la deuxième colonne vaille 2*la première et la dernière soit linéairement indépendante des autres :



...Peut être réécrit ainsi:



La matrice utilisée en exemple ne permet donc pas de générer davantage que des vecteurs qui "se trouvent sur un plan" (rang 2) si elle avait été de rang 3, elle aurait permis de générer tous les vecteurs qui auraient pu remplir le volume (R3). Si finalement toutes ses colonnes étaient multiples d'un seul vecteur, cette matrice n'aurait pas pu générer plus que des vecteurs posés sur une même ligne (réécrire l'exemple ci-dessus avec le dernier vecteur combinaison linéaire des deux autres pour le constater).

L'espace nul (corrigez-moi si je me trompe) est - selon les exemples ci-dessus - l'ensemble des vecteurs qu'il est possible d'ajouter à la colonne manquante de la dernière matrice pour pouvoir "remplir" tout Rn (passer à det(A) != 0), n étant le nombre de dimensions des vecteurs colonne. Pour trouver ces vecteurs, je crois qu'il faut trouver tous les vecteurs dont le produit scalaire avec tous les vecteurs colonne de la matrice sont nuls.

Je le sais bien, mon vocabulaire mathématique n'est pas très adapté aux yeux des puristes et je m'en excuse. Pourtant, je sais qu'il est possible de visualiser bien des propriétés des matrices (au moins jusqu'au rang 3). Se contenter des définitions par coeur et de les utiliser où cela s'impose serait dommage. Avoir l'intuition sur ce qui se produit c'est quand-même moins barbant

Cordialement
-----

[herrmattoon]

...Je crois bien que le produit scalaire ne permette pas de trouver l'espace nul d'une matrice étant donné que les vecteurs ne doivent pas nécessairement être orthogonaux pour étendre l'espace... Me souviens plus de la méthode

[gg0]

Désolé, Hermatoon, mais GBZM a raison, ce que tu avais écrit n'a rien à voir avec les mathématiques.
Le noyau de la matrice est l'ensemble des vecteurs qui, multipliés par la matrice, donnent le vecteur nul (d'où le nom "espace nul"). Rien à voir avec ce que tu racontes.

C'est bien gentil de vouloir aider, encore faut-il comprendre la question ... Et avoir les idées claires (tu avoues que ce n'est pas le cas).

Cordialement.

[Nini42]

herrmattoon si tu prends la matrice , tu peux remarquer que, sauf erreur, l'espace nul et l'image n'engendrent pas l'espace entier.

[A voir en vidéo sur Futura]

[herrmattoon]

Hello à tous,

Merci pour vos retours courtois

Effectivement, je n'ai vraiment pas les mots adéquats pour communiquer sur le sujet. Pour illustrer, cette fois-ci, ce que j'ai maladroitement exprimé plus haut, je laisse s'exprimer une image qui provient d'ici :
https://ocw.mit.edu/courses/res-18-0...inear-algebra/

A savoir celle-ci :



Où l'on peut mieux voir la relation entre les dimensions de l'espace nul (de dimension n-r) et celles de l'espace des lignes de A (de rang r).
De même, à droite, on constate que le "left null space" et l'espace des colonnes étendent à eux deux l'espace Rm de la matrice, étant perpendiculaires l'un par rapport à l'autre.

Le noyau de la matrice est l'ensemble des vecteurs qui, multipliés par la matrice, donnent le vecteur nul

Donc en partant de cette définition, selon l'exemple de Nini42 le vecteur [1 0 0]^T serait l'un des vecteurs du noyau de la matrice ? En effet, si je procède à la multiplication, j'obtiens le vecteur 0 :



Revenant sur l'image, le vecteur de l'espace nul ci-dessus est clairement perpendiculaire à toutes les lignes de la matrices puisque son produit scalaire avec chacune d'entre elles donne zéro. Autrement dit, il se place dans l'espace "null space" en bas à gauche dans l'image. L'espace qui lui est perpendiculaire est celui d'au-dessus, le "row space".

De même, si je trouve un vecteur ligne qui multiplie la matrice à gauche et qui donne le vecteur [0 0 0], j'aurai trouvé un vecteur de l'espace perpendiculaire à toutes les colonnes de la matrice (column space), autrement dit un vecteur qui appartient à l'espace "left null space" en bas à droite.

Si maintenant je remplace une ligne de la matrice qui est linéairement dépendante par le vecteur appartenant à l'espace nul, j'augmente le rang de la matrice. De même, si je remplace une colonne linéairement dépendante par l'un des vecteurs du left null space.

Est-ce que mes réflexions ne font réellement pas de sens ? Dans tous les cas c'est là où je voulais en venir dans mes messages précédents.

Cordialement.

[Deedee81]

Salut,

Je me demande s'il n'aurait pas été préférable d'ouvrir un nouveau sujet plutôt que de risquer d'induire un étudiant en erreur. on peut cliquer sur le triangle pour demander de scinder si tu veux

[albanxiii]

Je me demande s'il n'aurait pas été préférable d'ouvrir un nouveau sujet plutôt que de risquer d'induire un étudiant en erreur. on peut cliquer sur le triangle pour demander de scinder si tu veux

En effet, il est préférable de scinder le fil initial, c'est ce que j'ai fait.

[Nini42]

Effectivement, je n'avais pas compris que tu parlais de l'espace engendré par les lignes... Dans ce cas, comme tu le dis, les espaces sont complémentaires

[GBZM]

Bonjour,

Que veut dire "espaces complémentaires" ? À mon avis, ça n'a pas de sens.
Ce qu'explique la vidéo du MIT, c'est que le noyau (à droite) est le supplémentaire orthogonal de l'espace des lignes, et le noyau à gauche le supplémentaire orthogonal de l'espace des colonnes. Mais il est sous-entendu qu'on travaille avec des matrices à coefficients réels, car ça se gâte sérieusement si on travaille avec d'autres corps. Par exemple, sur , le noyau (à droite) de est égal à son espace des lignes !

[Nini42]

Je me suis en effet mélangé les pinceaux, je voulais dire supplémentaire...

[herrmattoon]

Bonjour,

Cette démo m'a rendu perplexe, étant donné que je ne suis pas familier avec les matrices complexes. Si je ne me trompe pas (corrigez-moi au besoin), il me semble que le produit scalaire de deux vecteurs dans le corps des complexes se calcule ainsi :



Or, selon la matrice donnée en exemple, une ligne multipliée avec l'une ou l'autre des lignes donne un produit scalaire nul (éléments du vecteur nul).

Si je le réécris de la manière suivante :



Sur la base de la définition du produit scalaire donnée plus haut, on constate que les éléments du vecteur nul sont en fait le résultat du produit scalaire des lignes de la matrices avec le vecteur A mon avis le conjugué complexe des vecteurs du noyau de cette matrice font bien partie de l'espace perpendiculaire à l'espace des lignes de cette matrice.

Faut-il encore que l'expression du produit scalaire dans Que j'ai donnée plus haut soit correcte.