Bonjour,
Dans N,
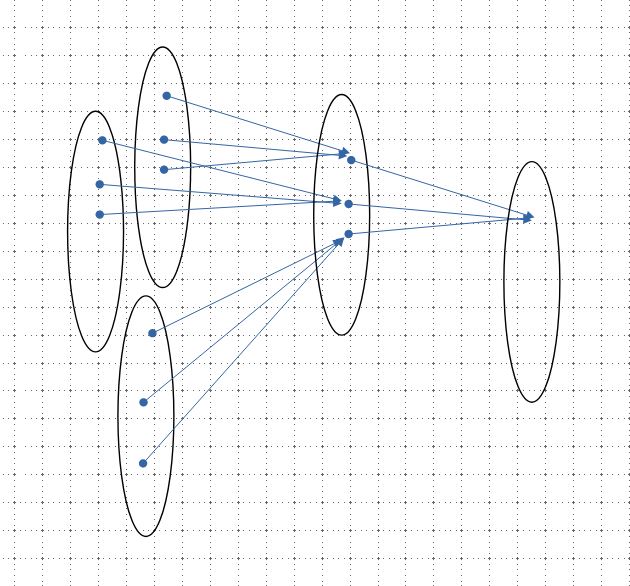
soit A1,...,An,... une infinité de sous-ensembles de N, chacun de cardinal infini, disjoints deux à deux, et l'union de tous ces ensembles est N. On considère f, l'application telle que pour tout i dans N, fi associe un unique élément de An à An+/-k, k élément de N et tel que n+/-k > ou = à 1.
Quelles sont les propriétés d'une telle "structure" ?
Sans questions il n'y a que des problèmes sans réponses.
Bonsoir Liet Kynes,
Que signifie le passage suivant :
?Envoyé par Liet Kynes
Cordialement.
L'application donne une unique image d'un élément de An dans An+/-k pour tout i élément de N
Sans questions il n'y a que des problèmes sans réponses.
Donc il n'y a pas de fi ... puisque tu dis "l'application" et qu'il n'y a qu'une seule application : f.
Du coup, la suite ne veut rien dire !! On ne sait pas qui est k. Pire, f ne peut envoyer un élément de A5 (n=5) à la fois dans A3 et dans A7 (k=2) puisqu'ils sont disjoints !
Et, question bête, tu connais une situation de ce genre ? Enfin, de ce que tu as dans la tête, parce que ce que tu as écrit est du non sens.
Dernière modification par gg0 ; 22/12/2022 à 20h57.
Bonsoir,
Voici ce que je pense,
On a,, par la bijection,
On peut donc prendre, pour tout,
Soit
Edit : Grillé par gg0.
Ah il y a de l'affinage à faire du coup.. c'est hyper difficile à formuler ce truc (enfin pour moi).. je traite le problème de f et de k et je reviens merci pour les premiers retours.
Sans questions il n'y a que des problèmes sans réponses.
Ton
Enfin, on écrira,
L'idée en écrivant de An vers An+/-k c'est de dire que f est une surjection de An vers un ensemble qui ne soit pas inclus dans An donc qu'ils sont disjoints.
L'application f contient une ou plusieurs variables liées à l'élément de départ.
Le schémas ci-dessous donne une idée*:
Sans questions il n'y a que des problèmes sans réponses.
Rien d'exceptionnel dans ton schéma !! Par contre, tes explications ("L'application f contient une ou plusieurs variables liées à l'élément de départ") sont toujours de la plus haute fantaisie, faute de l'utilisation de ta part du vocabulaire élémentaire de seconde de lycée. Arrête d'employer des mots que tu ne connais pas , c'est ridicule ! Tu recommence comme il y a quelques années ...
Soit tu as une idée floue, alors donne des exemples simples de ce que tu veux, soit tu n'as même pas d'exemple, et ta priorité devrait être de clarifier tes idées jusqu'à ce que tu puisses les écrire clairement ("Ce qui se conçoit bien s'énonce clairement). Et pour ça, apprends les maths qu'on apprend à 15 ans.
Oui, je suis le premier à en être gêné, j'ai été formé après les réformes de 70 (https://fr.wikipedia.org/wiki/Math%C...rnes_en_France) et j'ai ancré en lieu et place de certaines incohérences enseignées à cette époque des idées personnelles encore plus incohérentes :
je ne suis pas passé par un système d'enseignement de qualité (5 profs de maths en 3ème ) et la majorité étaient mal formés... ils n'y pouvaient rien non plus.
Les définitions que j'ai des choses sont donc dysfonctionnelles : il aurait été plus simple que je ne passe pas par la case collège-lycée dans ma vie pour apprendre correctement aujourd'hui.
Donc du coup une application c'est quoi ?
Sans questions il n'y a que des problèmes sans réponses.
il y a plusieurs définition de ce qu'est une application. Dans la tradition française une application est un triplet (A,B,f) où A est appelé ensemble de départ, B ensemble d'arrivée et où f est une partie de l'ensemble AxB (qui est l'ensemble des couples {a,b} avec a dans A et b dans B) telle que pour chaque a de A, f contienne un unique couple de la forme {a,b} b quelconque. En d'autres termes, f donne une image unique à chaque élément de A.
mais une autre tradition définit f comme un ensemble de couples {a,b}, avec toujours la même restriction : pour chaque a il n'y a qu'un seul couple {a,b}. L'ensemble de départ est simplement la réunion des membres de gauche des couples et on ne définit pas d'ensemble d'arrivée, mais un "range" (en angais) qui est la réunion des seconds membres des couples.
Bonsoir Liet Kynes,
D'après ton dessin ( i.e : schéma ) que tu as mis, ta nouvelle structure est déjà connu en mathématiques, particulièrement, en théorie des catégories, et géométrie algébrique. C'est une notion très importante en mathématiques et s'appelle : système inductif ( Voir ici : https://fr.wikipedia.org/wiki/Limite_inductive ). Il existe une notion duale à la notion de système inductif qui lui ressemble. C'est un système projectif ( Voir ici : https://fr.wikipedia.org/wiki/Limite_projective ).
Cordialement.
Merci à vous, j'y vois un peu plus clair dans mes idées, les systèmes inductif et projectifs sont hors de mon niveau.
La définition anglaise est plus parlante, "un seul couple {a,b}" c'est ce qui donne la notion d'unicité ? b peux être le même pour tout les a pourvus que tous les a soient différents ?
L'union de plusieurs ensembles peut être définie par une application ?
Sans questions il n'y a que des problèmes sans réponses.
Bonjour.
L'anonyme est très fort pour trouver des grands noms, mais comme toi-même ne sais pas de quoi il s'agit, il n'y a aucune chance que ce soit adapté. Et comme il mélange système inductif et limite inductive (deux notions sans rapport direct), il raconte n'importe quoi comme d'habitude. mais il aime étaler ses connaissances (les mots, il ne sait rien en fait).
La notion d'application est élémentaire c'est intuitivement l'idée : à chaque objet j'associe un et un seul objet, son image. Et comme d'habitude, si on dit "pour un a donné, un seul couple (a,b)", donc un seul b, ça ne dit rien de a. Le fait que tu poses la question montre qu'après des années à parler avec des matheux, tu n'acceptes toujours pas de ne donner à leurs phrases que le sens précis qu'elles ont, tu continues à penser en poète.
"L'union de plusieurs ensembles peut être définie par une application ? " prise strictement ta phrase appelle la réponse oui (il est possible qu'une application serve à définir une réunion d'ensembles). Après, vu ton manque de prise en compte des mots, il n'y a pas de réponse à une question écrite trop imprécisément.
J'affine avec mon peu de moyens certaines connaissances, j'ai l'impression que derrière ce qui parait très simple se cache souvent du très compliqué. Et c'est vrai que certains esprits fonctionnent un peu de façon inattendue, mais cela peut quand même fonctionner
Pour illustrer, dans ma procrastination (mon sujet habituel dans ces forums) , j'ai trouvé une des applications qui me manquait ce matin avec la formule ((((3^a-2^a)*2^(((2*(3^(a-1)))-a))*2^a)-(3^a-2^a))/3^a) ben dans l'idée le résultat est plus compliqué que ce qu'il n'y paraissait au moment où je me posai la question de la trouver et je suis bien incapable de savoir pourquoi je l'ai trouvé, je sais juste comment j'ai fait mais pas pourquoi: ceux qui font vraiment des maths savent les deux.
Du coup pour revenir dans le sujet les éléments d'un ensemble peuvent être formés à partir d'une application "interne" à l'ensemble ? (Je ne sais pas si c'est le bon mot)
Dernière modification par Liet Kynes ; 24/12/2022 à 15h27.
Sans questions il n'y a que des problèmes sans réponses.
Désolé, mais ta question n'a aucun sens. Si tu veux dire par "interne" une application de l'ensemble dans lui-même, alors l'application nécessite les éléments de l'ensemble pour être définie, donc ces éléments "préexistent" à l'application. par contre, une application de E dans E définit certains éléments de E, globalement, par le fait que ce sont des images. par exemple, l'application de N dans N donnée par f(n)=2n "définit" les entiers pairs.
Je remarque que tu continues à employer de travers le vocabulaire; ce que tu appelles "formule" - ((((3^a-2^a)*2^(((2*(3^(a-1)))-a))*2^a)-(3^a-2^a))/3^a) - est une expression, tout à fait simplifiable par factorisation. Mais peut-être voulais-tu dire une incantation, une formule cabalistique, un équivalent de "abracadabra"; en tout cas ce n'est pas une formule mathématique. Et en plus tu dis "
Pour illustrer, dans ma procrastination (mon sujet habituel dans ces forums) , j'ai trouvé une des applications qui me manquait ce matin avec la formule" ?? Une application de la formule ? Ou bien une application au sens mathématique, une fonction ? Tu baratines trop pour qu'on puisse te comprendre ! Mais est-ce ton objectif ? Ou bien le fait d'écrire ici te suffit à faire grossir ton égo ?
Bof mon égo on s'en fiche pas mal d'ailleurs avec toutes les conneries que j'ai pu écrire il est pas mal écorné
Ta réponse me fait comprendre une erreur d'interprétation que j'ai, il faut que je travaille dessus.
Sans compter les confusions que j'ai avec les notions de suite.
Pour l'expression du post d'avant:
Ce n'est pas poli de ne pas expliquer et en même temps mes explications sont si souvent mal dites que c'est quasi tout aussi impoli de les donner, le but pour moi reste d'énoncer clairement un raisonnement donc pour l'instant j'exprime maladroitement.
En grossissant le trait, l'expression " ((((3^a-2^a)*2^(((2*(3^(a-1)))-a))*2^a)-(3^a-2^a))/3^a) " est le "1" dans le 4x+1 pour Collatz le 4 étant (x*(2^(2*(3^(a-1)))))
Cela donne (x*(2^(2*(3^(a-1)))))+((((3^a-2^a)*2^(((2*(3^(a-1)))-a))*2^a)-(3^a-2^a))/3^a) qui bien écrit (merci wolfram) : 4^(3^(a - 1)) (-(2/3)^a + x + 1) + (2/3)^a - 1 ,
la suite générée pour un couple (x,a) a étant la valuation 2 adique de x+1, x étant impair, donne des nombres qui convergent tous vers le même résultat.
Par exemple pour 31, v2(x+1)=5 , 31 converge vers 121 avec (((3^a*x)+(3^a-2^a))/2^a)/2^b avec a et b à choisir judicieusement comme vu dans d'autres posts (pour 31, a=5 et b=1)
4^(3^(5- 1)) (-(2/3)^5+ 31+ 1) + (2/3)^5- 1= 186302365094494027959989059169 627912826593277577055 ce nouveau nombre u(n+1) converge vers 121 sa valeur de b est celle du b de 31 + 2*(3^(a-1)) et si je réapplique à ce nombre la fonction 4^(3^(a - 1)) (-(2/3)^a + x + 1) + (2/3)^a - 1 à ce nombre le nouveau nombre converge aussi vers 121. La valeur de b de u(n+1) est simplement celle de b de u(n) + 2*(3^(a-1)) et a est une constante*:
(((3^5*18630236509449402795998 9059169627912826593277577055)+ (3^5-2^5))/2^5)/2^(1+(2*(3^(5-1)))=121
Sans questions il n'y a que des problèmes sans réponses.
