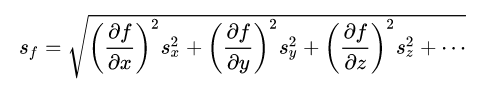propagation d'incertitude d'un système d'équations asphérique vs ellipse

[vadg]

Bonjour

J'ai une définition d'une asphérique avec une spécification en Rayon et en Constante conique.
R=R_cible+/-∆R=80+-0.1mm et k=k_cible+/-∆k=0.5+/-0.03

J'aimerai passer ces spécifications dans la définition ellipsoïdal de mon asphérique.
On a effectivement le rayon du grand axe et du petit axe : a=R/(1+k) et b=R/√(1+k).
Je veux connaitre les incertitudes autorisées sur "a" et "b".

Par la loi de propagation des incertitudes, on a : ∆a=√((∂a/∂R ∆R)^2+(∂a/∂k ∆k)^2 )=√((1/(1+k) ∆R)^2+(-R/(1+k)^2 ∆k)^2 ) et/ou
∆b=√((∂b/∂R ∆R)^2+(∂b/∂k ∆k)^2 )=√((1/√(1+k) ∆R)^2+(-R/〖2(1+k)〗^(3/2) ∆k)^2 )

Mais je suppose que ça signifie qu'on s'autorise à avoir une ellipse définit par :
- a=a_cible+/-∆a=R_cible/(1+k_cible)+/-∆a et b=b_cible (b sans incertitude).
- ou alors a=a_cible (a sans incertitude) et b=b_cible+/-∆b

On a donc le système d'équation définissant l'ellipse par les paramètres asphériques (R+/-∆R;k+/-∆k) qui peut être retranscrit en système d'équation définissant l'ellipse par les paramètres elliptiques (a+/-∆a;b) ou (a;b+/-∆b).
Sauf que j'aimerai que le système d'équation définissant une ellipse comporte avec à la fois les incertitudes sur "a" et sur "b" : (a+/-∆a;b+/-∆b).

J'espère avoir été clair...
Merci
-----

[gg0]

Bonjour.

Je ne comprends pas tout à tes calculs, mais je ne vois pas pourquoi tu dis que l'ellipse est définie avec a ou b sans incertitude. Ta supposition n'a aucune raison. la propagation d'incertitude suppose les nouvelles valeurs calculées avec les anciennes; qui servent aussi à calculer les nouvelles incertitudes en complément des incertitudes.

Cordialement.

[vadg]

Bonjour,

On a la loi de propagation des incertitudes (avec s l'ecart type, noté ∆ dans mon précédent message) :


J'utilise aussi le site suivant pour automatiser les calculs : https://nicoco007.github.io/Propagat...ty-Calculator/

Si on applique les formules et leurs applications numériques, j'ai mon asphérique définit par (R+/-∆R;k+/-∆k)=(80+-0.1;0.5+/-0.03) qui devrait être équivalent à la définition en ellipse (a+/-∆a;b+/-∆b)=(53+-1;65.3+/-0.7).
Ca ne me semble pas correct, tout simplement car si on essaie de faire le retour inverse, en imaginant qu'on a les valeurs des incertitudes en définition elliptique (a+/-∆a;b+/-∆b)=(53+-1;65.3+/-0.7) et qu'on veut les retranscrire en définition asphérique (R+/-∆R;k+/-∆k); alors en appliquant le même procédé, cette fois ci on trouve (R+/-∆R;k+/-∆k)=(80+-2;0.5+/-0.07). Ce qui n'est pas du tout équivalent à ce qu'on avait au départ : (R+/-∆R;k+/-∆k)=(80+-2;0.5+/-0.07) a des incertitudes beaucoup plus grandes que (R+/-∆R;k+/-∆k)=(80+-0.1;0.5+/-0.03).

Ce qui me fait dire que pour un "système d'équation", la propagation d'incertitude est un peu différent...

Merci

[gg0]

Mais la propagation d'incertitude n'a aucune raison d'être réversible !! D'ailleurs elle a le gros inconvénient d'augmenter en fait l'incertitude. C'est ce que tu constates.

Cordialement.

[A voir en vidéo sur Futura]