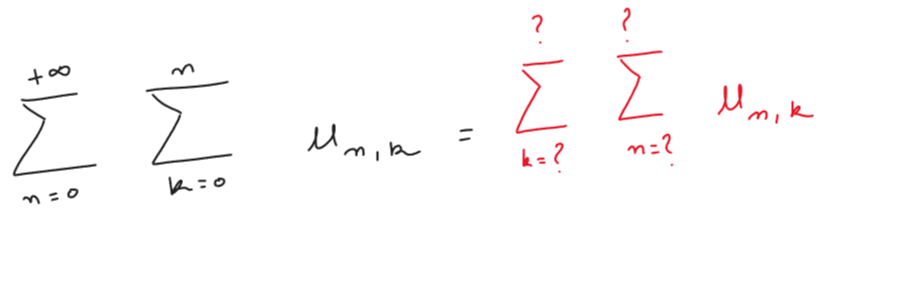Bonsoir,
svp je sais pas comment procéder pour justifier qu on peut intervertir les deux sommes dans ce cas, déja c'est quoi la condition pour pouvoir les intervertir?puis que sera l'expression(càd les indices)?
Je sais qu'il y a le theoreme de FUBINI qui s'interesse à l interversion des sommes mais dans le theoreme on a deux sommes infinies!
Veuillez aussi citer d'autres cas de sommation et les conditions qu'on doit satisfaire pour faire l'interversion.
Merci.
Dernière modification par itslunyitsluny ; 14/01/2023 à 22h35.
Bonjour.
Mauvaise lecture, je reviens.
En changeant éventuellement d'indice, on a deux sommes de 0 à m et n. La règle est simple : Tous les termes d'indices concernés apparaissent une fois et une seule :
En fait, dès qu'on décode la notation de la somme double, on sait. Et la justification est la commutativité et l’associativité de l'addition (valable pour les sommes finies).
Cordialement.
Dernière modification par gg0 ; 15/01/2023 à 08h18.
je sais pas pourquoi l image n apparait pas,en tout cas je crois que maintenant ca fonctionne.
comment intervertir cette somme et c'est quoi la condition?
y a t il d autres cas que je dois connaitre?
Tu peux appliquer les règles pour les séries en posant u_{n,k} = 0 si k>n et écrivant la deuxième somme comme une série. Mais sans ce genre de convention, tu ne peux pas inverser, puisque au départ, k dépend de n.
Cordialement.
donc on doit se rendre "toujours" au cas de deux sommes infinies puis on applique le fubini
Voyons !! Je traite un cas particulier que tu as proposé, tu en déduis une règle générale ?? Une règle établie sur 1 seul cas, ce n'est pas sérieux.
Réfléchis à bien comprendre ce qui se passe, puis, dans d'autres exercices, tu réfléchiras plus sérieusement à ce qui s'y passe. C'est ça, l'expérience, c'est l'habitude de penser sérieusement à ce qu'on a à faire. Les règles, tu en as déjà assez dans ton cours, à parfaitement connaître, pour ne pas en inventer.
je dis pas une regle mais au moins il va falloir retenir qqchose de cet exemple,et je vois que parfois il faut se ramener à deux sommes infinies pour appliquer ce qu on a dans le cours.Merci en tout cas.
Bien évidemment, se souvenir des exercices qu'on a fait est utile, mais tu écrivais "on doit se rendre "toujours" au cas..". Non, on n'est pas obligé d'imiter systématiquement.
Oui vous avez raison.
