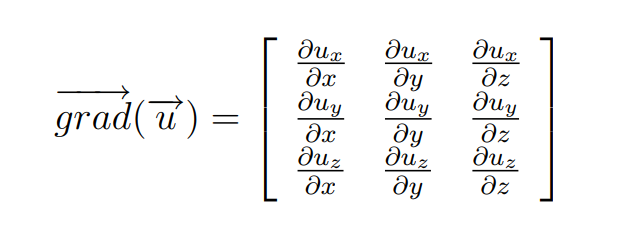Bonjour ma question est plutôt simple.
J'ai appris en maths que le gradient d'un vecteur donne cette matrice :
Ma question est la suivante : quelle est la démonstration pour l'obtenir ?
car j'ai essayé de la retrouver en faisant une multiplication comme pour les matrices, donc grad fois u, mais en appliquant les règles mathématiques liées à la multiplication de matrice je n'obtiens pas le résultat.
Est-ce que ma question est claire, et si oui est-ce que quelqu'un peut me l'expliquer simplement ? (une démonstration papier/ord sera plus simple qu'un texte je pense).
Merci beaucoup
-----