Portrait de phase

**leroisinge** · 10/02/2024, 23h51

Bonjour,

Je n'ai pas du tout compris la réponse à la question 8. Comment raisonne t'on ?

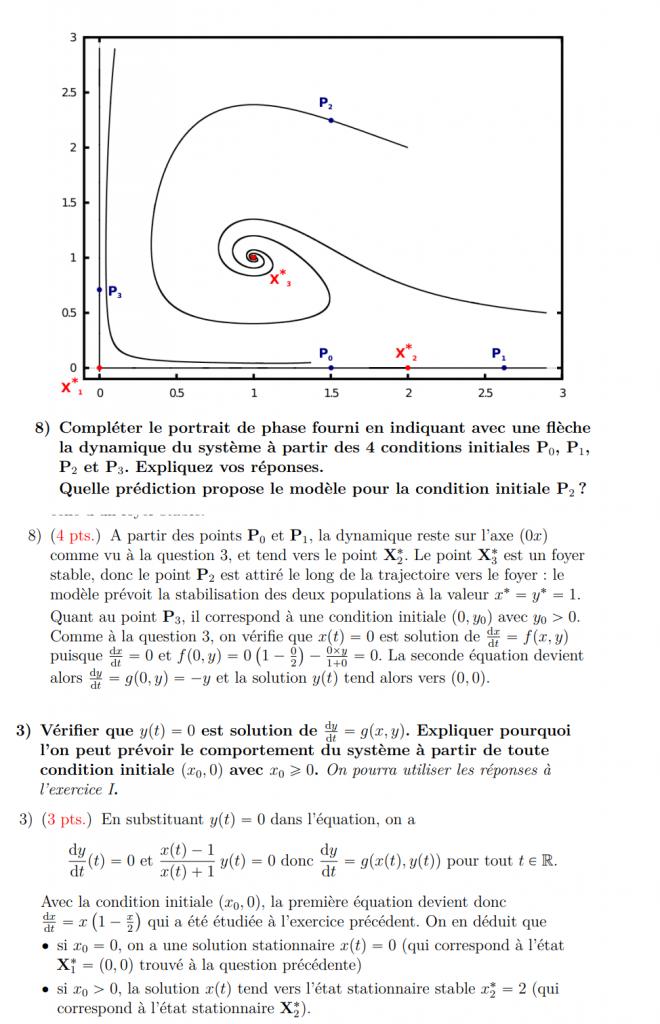
Au point X1* et X2* on a un point selle.
Au point X3*, on a un foyer stable.

Je vous joins également la réponse à la question 3.
Je ne sais pas si vous avez besoin de d'autres éléments pour répondre à la question.

Merci de votre attention

1 PJ :

Nom : question.jpg
Affichages : 129
Taille : 98,6 Ko

Nom : question.jpg
Affichages : 129
Taille : 98,6 Ko

**Anonyme007** · 11/02/2024, 00h59

Bonsoir,

- Est ce que tu peux préciser comment sont définis $\text{[math]}$ et $\text{[math]}$ telles que, $\text{[math]}$ ?
- Est ce que tu peux calculer ensuite le système linéarisé du système $\text{[math]}$ ?

Cordialement.

**Anonyme007** · 11/02/2024, 02h18

Envoyé par leroisinge

Comment raisonne t'on ?

On va aller étape par étape,
- Autour du point $\text{[math]}$ ,
L’image inséré dans ton corrigé nous apprend que $\text{[math]}$ et $\text{[math]}$ se trouvent sur l'axe $\text{[math]}$ , et se dirige vers le point $\text{[math]}$ . On dit que le point $\text{[math]}$ est un point attractif.
Le raisonnement suivi dans la réponse à la question $\text{[math]}$ du corrigé de ton exercice répond à la question : Est ce que cette conclusion faite ci-dessus à partir de l’image de ton exercice était à priori, prévisible et se déduisait directement par le calcul à partir de l'expression du système, $\text{[math]}$ .
La réponse est oui. En effet, ( Comme répondu dans ton corrigé d’ailleurs )
La question $\text{[math]}$ conclut que, autour de $\text{[math]}$ ( C'est à dire, lorsque, $\text{[math]}$ et $\text{[math]}$ ) $\text{[math]}$ qui tend vers $\text{[math]}$ et $\text{[math]}$ , sont solution au système, $\text{[math]}$ ( Vérifie le corrigé de la question qui précédait la question $\text{[math]}$ . C'est ce que ton corrigé précise. Il dit que si tu cherches l'expression de $\text{[math]}$ autour de $\text{[math]}$ , il faut retourner à la question qui précédait la question $\text{[math]}$ pour s’assurer qu'elle tend vers $\text{[math]}$ ).

============================== ==================

Je te laisse le soin de suivre la meme méthode de raisonnement,
- Autour du point $\text{[math]}$ ,
- Autour du point $\text{[math]}$ ,

Cordialement.

**Anonyme007** · 11/02/2024, 02h29

Envoyé par Anonyme007

L’image inséré dans ton corrigé nous apprend que $\text{[math]}$ et $\text{[math]}$ se trouvent sur l'axe $\text{[math]}$ , et se dirige vers le point $\text{[math]}$ . On dit que le point $\text{[math]}$ est un point attractif.

Pardon, je corrige,
L’image inséré dans ton corrigé nous apprend que $\text{[math]}$ et $\text{[math]}$ se trouvent sur l'axe $\text{[math]}$ , et se dirige vers le point $\text{[math]}$ . On dit que le point $\text{[math]}$ est un point attractif.

C’est $\text{[math]}$ et $\text{[math]}$ , et non, $\text{[math]}$ et $\text{[math]}$ .

A voir en vidéo sur Futura · Aujourd'hui

**leroisinge** · 11/02/2024, 13h48

Bonjour Anonyme007,

Merci de votre longue réponse.

Comment sait t'on, graphiquement, que P0 et P1 se dirigent vers X2* = (2,0)
(Je ne l'ai pas précisé, mais l'image fait partie de l'énoncé, et non du corrigé. C'est à dire que lors de l'exercice, j'ai accès à l'image).

Vérifie le corrigé de la question qui précédait la question . C'est ce que ton corrigé précise

Nous avons précédemment montré que X1*, X2* et X3* sont des états stationnaires du système.

D'ailleurs, dans la question 3, si x0>0 et y0=0, comment voit on que x(t) tend vers 2 ?
Est ce un calcul de limite ? Je n'en ai pas l'impression !

Je vais essayer d'avoir le même raisonnement pour X1* et X3*
Est ce que je dois, pour cela, réutiliser la question 3 ?

**Anonyme007** · 11/02/2024, 14h14

Bonjour leroisinge,

Envoyé par leroisinge

Comment sait t'on, graphiquement, que P0 et P1 se dirigent vers X2* = (2,0)
(Je ne l'ai pas précisé, mais l'image fait partie de l'énoncé, et non du corrigé. C'est à dire que lors de l'exercice, j'ai accès à l'image).

C'est le corrigé des questions qui précédaient la question $\text{[math]}$ qui le précise.

Envoyé par leroisinge

Nous avons précédemment montré que X1*, X2* et X3* sont des états stationnaires du système.

D'ailleurs, dans la question 3, si x0>0 et y0=0, comment voit on que x(t) tend vers 2 ?
Est ce un calcul de limite ? Je n'en ai pas l'impression !

C'est le corrigé des questions qui précédaient la question $\text{[math]}$ qui le précise. Montre nous ce corrigé que tu as oublié de nous insérer.

Envoyé par leroisinge

Je vais essayer d'avoir le même raisonnement pour X1* et X3*
Est ce que je dois, pour cela, réutiliser la question 3 ?

Même remarque. Montre nous ce corrigé des questions qui précédaient la question $\text{[math]}$ que tu as oublié de nous insérer.

Montre nous aussi comment est défini le système $\text{[math]}$ .

**leroisinge** · 11/02/2024, 15h03

Oh ! Pardon ! Je me rends compte qu'il vous manque les questions précédentes pour m'aider !

Voici les questions 1 à 8
question.jpg

Voici la solution
réponses.jpg

**Anonyme007** · 11/02/2024, 18h22

Voilà. D’accord. Merci.
Donc, le système $\text{[math]}$ est, $\text{[math]}$ .
Le point $\text{[math]}$ est un point stationnaire. ( On dit aussi un point d’équilibre ).
Pour étudier le comportement des trajectoires $\text{[math]}$ autour du point stationnaire $\text{[math]}$ suivant une condition initiale $\text{[math]}$ ( i.e, le portrait de phase autour du point stationnaire $\text{[math]}$ ), on linéarise le système $\text{[math]}$ autour du point stationnaire $\text{[math]}$ qui est un système linéarisé défini par la matrice $\text{[math]}$ du système $\text{[math]}$ , le portrait de phase du système initial $\text{[math]}$ et le portrait de phase de son linéarisé défini par la matrice $\text{[math]}$ sont identiques, d’après le théorème de Grobman-Hartman.
On étudie donc, le système linéarisé défini par $\text{[math]}$ à la place du système $\text{[math]}$ , parce que, ce système linéarisé est linéaire, donc facile à étudier, vu que les mathématiciens de nos jours disposent d'une théorie d'EDO qui permet d'étudier le portrait de phase du système linéarisé, alors que le système initial $\text{[math]}$ est non linéaire et donc très compliqué et difficile à aborder, et que de nos jours, on ne dispose pas d'une théorie capable de le traiter directement sans passer par le système linéarisé.
Voilà donc, on va étudier le portrait de phase du système linéarisé, $\text{[math]}$ , où, $\text{[math]}$ .
L'étude du portrait de phase du système, $\text{[math]}$ autour du point stationnaire $\text{[math]}$ consiste à étudier la nature du point stationnaire $\text{[math]}$ à partir de l'étude de la matrice $\text{[math]}$ , qui comprend les étapes énumérés à la page, 27-28 du pdf suivant, https://www.imo.universite-paris-sac...P2S3-Chap7.pdf . Tu verras après quelques petits calculs, qu'il s'agit effectivement d'un point selle, et par la suite, on peut donc dessiner le portrait de phase autour de ce point selle, c'est à dire l’allure approximative des trajectoires $\text{[math]}$ passant par n’importe quelle condition initiale $\text{[math]}$ se trouvant proche de $\text{[math]}$ sur l’image de ton exercice.
Voilà. Donc, je t'ai tout expliqué. Retourne aux deux pages du pdf que je t'ai indiqué et essaye de suivre ses indictions pour établir qu'il s’agit en fait d'un point selle. $\text{[math]}$ est un point selle.

**leroisinge** · 11/02/2024, 19h27

Merci d'avoir pris le temps de m'écrire !

J'ai compris que X2* était un point selle.

Comment sait t'on, graphiquement, que P0 et P1 se dirigent vers X2* = (2,0)
(Je ne l'ai pas précisé, mais l'image fait partie de l'énoncé, et non du corrigé. C'est à dire que lors de l'exercice, j'ai accès à l'image).

Est ce que cela explique que P0 et P2 se dirigent vers X2* ? En fait je n'ai pas compris le raisonnement, et le lien avec les questions précédentes.

D'ailleurs, dans la question 3, si x0>0 et y0=0, comment voit on que x(t) tend vers 2 ?
Est ce un calcul de limite ? Je n'en ai pas l'impression !

Je vous repose cette question !

**Anonyme007** · 11/02/2024, 21h17

Envoyé par leroisinge

J'ai compris que X2* était un point selle.
Comment sait t'on, graphiquement, que P0 et P1 se dirigent vers X2* = (2,0)
(Je ne l'ai pas précisé, mais l'image fait partie de l'énoncé, et non du corrigé. C'est à dire que lors de l'exercice, j'ai accès à l'image).
Est ce que cela explique que P0 et P2 se dirigent vers X2* ? En fait je n'ai pas compris le raisonnement, et le lien avec les questions précédentes.

- Si $\text{[math]}$ , alors, $\text{[math]}$ est un point attractif.
- Si $\text{[math]}$ , alors, $\text{[math]}$ est un point répulsif.
Regarde ici, https://www.imo.universite-paris-sac...P2S3-Chap7.pdf , page, 14 pour en savoir plus.

Envoyé par leroisinge

D'ailleurs, dans la question 3, si x0>0 et y0=0, comment voit on que x(t) tend vers 2 ?
Est ce un calcul de limite ? Je n'en ai pas l'impression !

En résolvant le système linéaire, $\text{[math]}$ , on obtient l'expression de $\text{[math]}$ et l'expression de $\text{[math]}$ .
Dans ce cas là, on peut en conclure que $\text{[math]}$ tend vers $\text{[math]}$ lorsque $\text{[math]}$ tend vers $\text{[math]}$ ou $\text{[math]}$ suivant si $\text{[math]}$ est un point attractif ou un point répulsif.

**Anonyme007** · 11/02/2024, 21h49

Pardon. je corrige.

En résolvant le système linéaire, $\text{[math]}$ , on obtient l'expression de $\text{[math]}$ et l'expression de $\text{[math]}$ .
Dans ce cas là, on peut en conclure que $\text{[math]}$ tend vers $\text{[math]}$ lorsque $\text{[math]}$ tend vers $\text{[math]}$ ou $\text{[math]}$ suivant si $\text{[math]}$ est un point attractif ou un point répulsif.

**leroisinge** · 11/02/2024, 23h22

Je n'arrive pas à citer votre message.

Vous dites que si la limite en + l'infini de X(t) est X2*, alors X2* est un point attractif. Si la limite en - l'infini de X(t) est X2*, alors X2* est un point répulsif.
Mais, alors, si la limite (en plus ou moins l'infini) n'est pas X2*, mais X1*, ou autre chose, alors, qu'est ce que c'est ?

Pouvez vous me montrer, dans le cadre de mon exercice, comment la limite de X(t) en + l'infini est X2* ? je n'arrive pas à le comprendre

**Anonyme007** · 11/02/2024, 23h38

Envoyé par leroisinge

Vous dites que si la limite en + l'infini de X(t) est X2*, alors X2* est un point attractif. Si la limite en - l'infini de X(t) est X2*, alors X2* est un point répulsif.
Mais, alors, si la limite ( en plus ou moins l'infini) n'est pas X2*, mais X1*, ou autre chose, alors, qu'est ce que c'est ?

Si la limite ( $\text{[math]}$ en $\text{[math]}$ ) n'est pas $\text{[math]}$ , mais $\text{[math]}$ , ou autre chose, ça voudrait dire que, $\text{[math]}$ est solution du système linéaire, $\text{[math]}$ et non du système linéaire, $\text{[math]}$ , ce qui est absurde, car $\text{[math]}$ est bel et bien solution du système $\text{[math]}$ .

Envoyé par leroisinge

Pouvez vous me montrer, dans le cadre de mon exercice, comment la limite de X(t) en + l'infini est X2* ? je n'arrive pas à le comprendre

Il faut résoudre le système linéaire, $\text{[math]}$ pour trouver l'expression de $\text{[math]}$ , sinon, tu ne pourras pas calculer la limite de $\text{[math]}$ en $\text{[math]}$ ou en $\text{[math]}$ et trouver finalement que c'est $\text{[math]}$ .

**leroisinge** · 08/04/2024, 15h52

Bonjour,

Je me rend compte que je n'ai pas répondu à votre message.
J'ai passé mon contrôle de mathématiques il y a plus d'un mois, et j'ai obtenu 20/20.

Merci beaucoup pour votre aide.
A bientot sur le forum

Portrait de phase