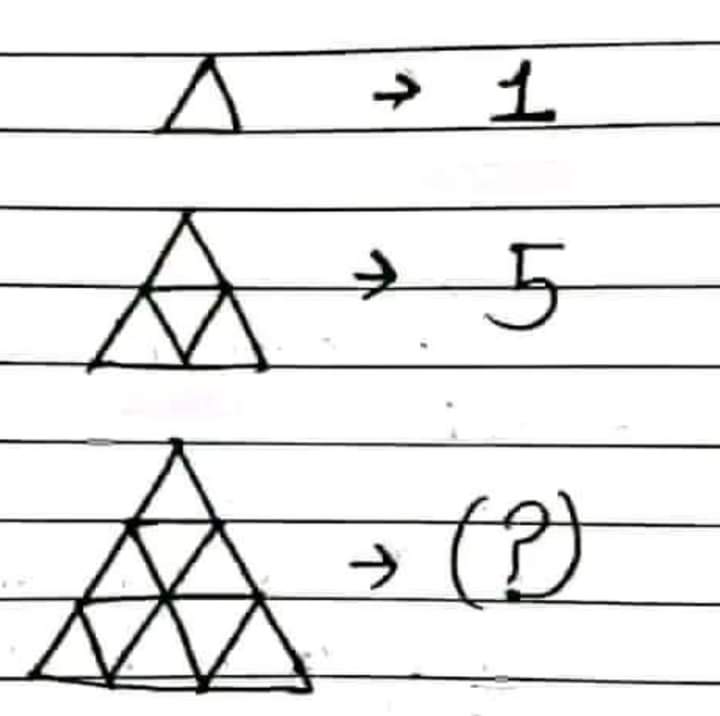Nombre de triangles

[Titiou64]

Bonjour,

Sur un groupe d'énigmes mathématiques, j'ai vu passer cette image demandant le nombre de triangle dans la figure avec 3 lignes. (je vous laisse chercher la réponse à titre d'échauffement )
Ma question est comment généraliser une formule permettant de trouver le nombre total de triangles dans une figure avec n lignes.



J'en suis là de mes réflexions :
Soit N le nombre de triangles pour n lignes.
J'ai déterminé que N(n)= N(n-1) (nombre de triangles avec n-1 lignes) + (2n-1) [ nombre de petits triangles ajoutés) + (n-1) + (n-2) + ... + 1
Les (n-1), (n-2), ... correspondent à chaque fois au nombre de triangles de plus en plus grands.

Donc N(n) = N(n-1) + (2n-1) + (n-1)*n/2 = N(n-1) + (4n-2+n²-n)/2 = N(n-1) + (n²+3n-2)/2.

J'en arrive donc à une suite définie par récurrence avec N(1) = 1 et N(n) = N(n-1) + (n²+3n-2)/2.

Comment passer à une forme explicite pour cette suite?

Merci pour vos retours
-----

[MissJenny]

tous les triangles ont deux points sur la même ligne et le troisième point soit au-dessus soit au-dessous. Le point du dessus existe toujours mais le point de dessous n'existe pas forcément, il existe si la ligne des deux points est k lignes au-dessus de la ligne du bas et les deux points espacés d'au plus k intervalles (k>0). C'est peut-être plus facile de compter de cette façon (?)

[Biname]

Salut,
Très vieux problème
https://youtu.be/9EU3FlKj-3M 4 minutes

Si n est le nombre de bases de petits triangles sur la grande base



Verif :

n = 1 ==> int[n.(n + 2)(2.n + 1)] 
n = 1 ==> int[1.(1 + 2)(2.1 + 1)] = int[1 * 3 * 3/8] = 1
n = 2 ==> int[2.(2 + 2)(2.2 + 1)] = int[2 * 4 * 5/8] = 5
n = 3 ==> int[3.(3 + 2)(2.3 + 1)] = int[3 * 5 * 7/8] = 13
27, 48, 78, ...

[titijoy3]

voir ici ? :https://major-prepa.com/mathematique...er-recurrence/

on observe qu'a chaque itération on augmente de deux le nombre de triangle entre deux ligne

[A voir en vidéo sur Futura]