Bonjour,
A 30 ans j'ai décidé de reprendre mes études que je combine avec mon boulot! Mon problème c'est que la physique et moi ça fait 2!
On viens de voir le courant continu, U=RI, loi des noeuds, loi des mailles, Norton Thévenins Milman: Mais on me demande de calculer i pour le schéma ci-dessous et je séche!
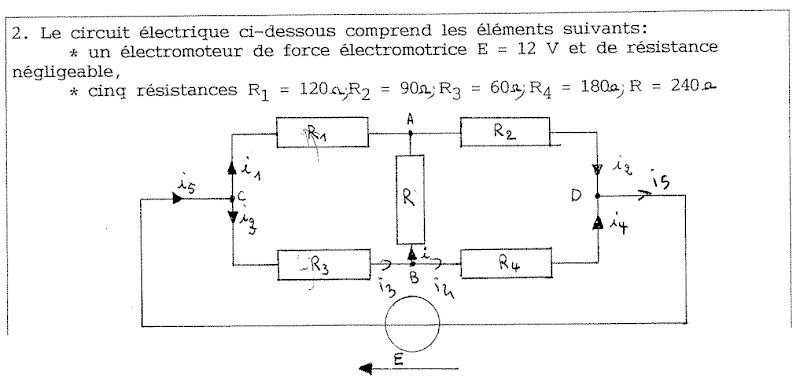
Bonjour,
Il faut appliquer la loi universelle de l'OHM en electricité
Point N°1 calculer le courant dans chaque maille ou resistance. Avec les sens des courants que tu as choisi
Vac = R1 I1 equation (E1)
dans R2 le courant provenant de R vient s'ajouter au courant I1
Vda = R2 (I1+ I) equation E(2)
Vbc = R3 I3 équation E(4)
dand R4 circule le courant I4 = I3-I
Vdb = R4 ( I3 - I ) equation E(5)
E = Vda + Vac equation E(6)
E = Vdb + V dc equation E(7)
il faut ajouter
Vab = R I equation E(8)
Les inconnues sont
I , I1,I2,I3, Vab, Vda, Vbc, Vdb donc 8 inconnue
Il faut donc resoudre ce système de 8 equations à 8 inconnues
Très bien de reprendre des études, félicitations.
Ceci dit, il ne faut pas se précipiter quand on a affaire à ce genre de problème. En particulier, il ne faut pas rajouter des inconnues partout comme tu as fait avec les i1, i3, i2 et i4, ça alourdit et ça augmente les chances d'erreurs.
Appelle I le courant dans E, i le courant dans R3 et i' le courant dans R. Tu verras qu'avec ça tu peux exprimer tous les courants.
Ensuite tu écris la tension entre C et D :
E = 120 (I-i) + 90 (I - i + i') si tu prends le courant i' dans R vers le haut.
Pareil la boucle du bas :
E = 60i + 180 (i-i')
Et enfin la boucle de gauche qui se referme donc :
0 = 120 (I-i) - 240 i' - 60 i
3 équations et 3 inconnues, ça se fait.
L'idée est la loi d'Ohm qui dit qu'entre 2 points A et B la chute de tension vA - vB est égale à R i - E si i est orienté de A vers B et si le signe de E est celui de la borne de sortie.
Bonjour.
La méthode proposé par Jeanpaul est bonne. Elle fonctionne et il faut avoir fait ce type de calcul plusieurs fois, pour être à l'aise.
Mais dans ce montage, et comme vous dites que vous avez fait les théorèmes de Norton et Thévenin, il y a une solution encore plus courte en faisant deux transformations.
-Doublez la source de tension idéale E en lui branchant une source identique en parallèle. Ceci ne change en rien ni les courants ni les tensions dans le reste du circuit.
-Maintenant utilisez une des sources E pour alimenter la branche R3 R4 et l'autre pour alimenter l'autre branche R1 R2 (il faut débrancher les connexions au point C).
-Débranchez R et calculez les circuits équivalentes de Thévenin vus entre B et D puis entre A et D.
Maintenant vous avez deux sources de Thévenin face à face connectées en D.
-Rebranchez la résistance R.
-Vous pouvez calculer directement le courant i dans R.
Ce type de simplification n'est pas toujours possible et dans ce cas il faut faire le calcul "à la dure", par la méthode générale décrite par Jeanpaul.
Le nombre d'équations est égal au nombre de mailles, c'est à dire "au nombre de trous dans la maille" si vous la regardez comme un filet de pêche.
Les deux façons de calculer le circuit donnent le même résultat (évidemment). Vous devriez essayer de le faire par les deux méthodes.
Au revoir.
Une technique qui pourra te permettre de trouver directement i5 :
Tu utilise la transformation triangle/etoile pour R, R1 et R2 et tu peux trouver directement la résistance équivalente de ton circuit.
Pour les autres intensités, il suffit de faire la loi des mailles avec le triangle R/R1/R3 et R/R2/R4.
Sinon Thévenin marche très bien comme l'a dit LPFR.
\o\ \o\ Dunning-Kruger encore vainqueur ! /o/ /o/
Je ne connais pas la transformation triangle/étoileEnvoyé par obi76
Bonjour,
Le plus difficile c'est de repérer les mailles. Les mailles doivent décrire tous les composants, on essaie de trouver le minimum de mailles. Pour cela mon truc c'est de suivre les lignes et de checker les composants jusqu'à ce que je les aie tous.
Pour ton problème je dirais :
3 mailles : (R,R1,R3)
(R,R2,R4)
(E,R3,R4)
Pour la troisième on peut aussi prendre (E,R1,R2), les résultats sont les mêmes.
Pour les mailles, la règle est :
Les tensions s'annulent dans chacune des mailles.
Il y a trois mailles donc il faut aussi voir les conditions de quatre noeuds (toujours un de plus que le nombre de mailles).
Pour commencer, on donne un sens aux courants, c'est pure convention, on leur donne le sens qu'on veut mais ici c'est imposé par l'énoncé. Le sens du courant va aussi donner le sens des tensions.
Pour les noeuds, la règle est :
Les courants s'annulent en chaque noeud.
En chaque noeud le courant s'annule. Donc par exemple i3=i+i4 il faut faire attention au sens des flèches.
De même, i5=i1+i3 et aussi i5=i2+i4.
et enfin i2=i1+i.
Il n'y a pas d'autre noeud donc on est sur la bonne voie : 4 noeuds, 3 mailles.
On peut maintenant poser les équations des mailles en tenant bien compte du sens des flêches :
Ri + R3i3 = R1i1
Ri + R2i2 = R4i4
E + R3i3 + R4i4 = 0
Et maintenant yapuka résoudre...
Bon courage.
chrisdec
Mon problème c'es que je n'ai aucun courant!
Salut,
essaye d'écrire (comme l'a dit Jeanpaul) les tensions aux bornes de chaque résistance en fonction des mêmes intensités I, I', et I0 par exemple. Une fois que tu aura fait ça, applique la loi des mailles, pour avoir une relation entre toutes tes intensités.
Citron_21:
C'est bon j'obtiens i=0.02A mais comment être sur!
Bonjour,
comme vous débutez voici une astuce également pour savoir le nombre maximum d'équations nécessaires pour décrire un réseau quelconque:
Vous comptez le nombre de branches (ici B=6), le nombre de noeuds (ici N=4) et le nombre de mailles indépendantes se déduit des 2 autres par:
M=B-N+1=6-4+1=3 mailles indépendantes
Vous aurez donc à écrire 3 équations de mailles et 4 équations de noeuds pour résoudre cet exercice.
C'est un bon réflèxe de faire cette première analyse qui prend quelques secondes.
Ensuite c'est du calcul.
Il faut toutefois toujours bien de regarder la topologie du circuit pour pouvoir y trouver une singularité permettant de simplifier encore plus la démarche de calcul.
Bonsoir,
Ah oui, tu n'as pas besoin de connaître la valeur des courants à l'avance, ils vont être calculés en résolvant le système d'équation. Je t'ai donné la méthode bestiale, celle qui serait appliquée par un progamme informatique. La méthode de Jean-Paul a l'avantage d'être plus simple et aussi plus élégante, mais les règles sont les mêmes.
J'ai fait une erreur en disant qu'il y a un toujours un noeud de plus que le nombre de mailles. La formule juste est celle donnée par Hulk28: Noeuds=Branches-Mailles+1
Voilà pour la partie électricité, le reste c'est des maths.
Christophe.
Bonjour,
Je souhaitais simplement vous dire!
Mon problème est ainsi solutioné!
