gain quadripole

[Abu Maria.]

salt
considerons le quadripole suivant:
(regarder la jointe)
merci

-----

[b@z66]

Oui??? Et c'est quoi, la question?

PS: les formes d'usage sont peut-être là(Bonjour et Merci) mais le style télégraphique, très peu pour moi.

[b@z66]

Je vais faire un petit effort en me montrant généreux, malgré tout.

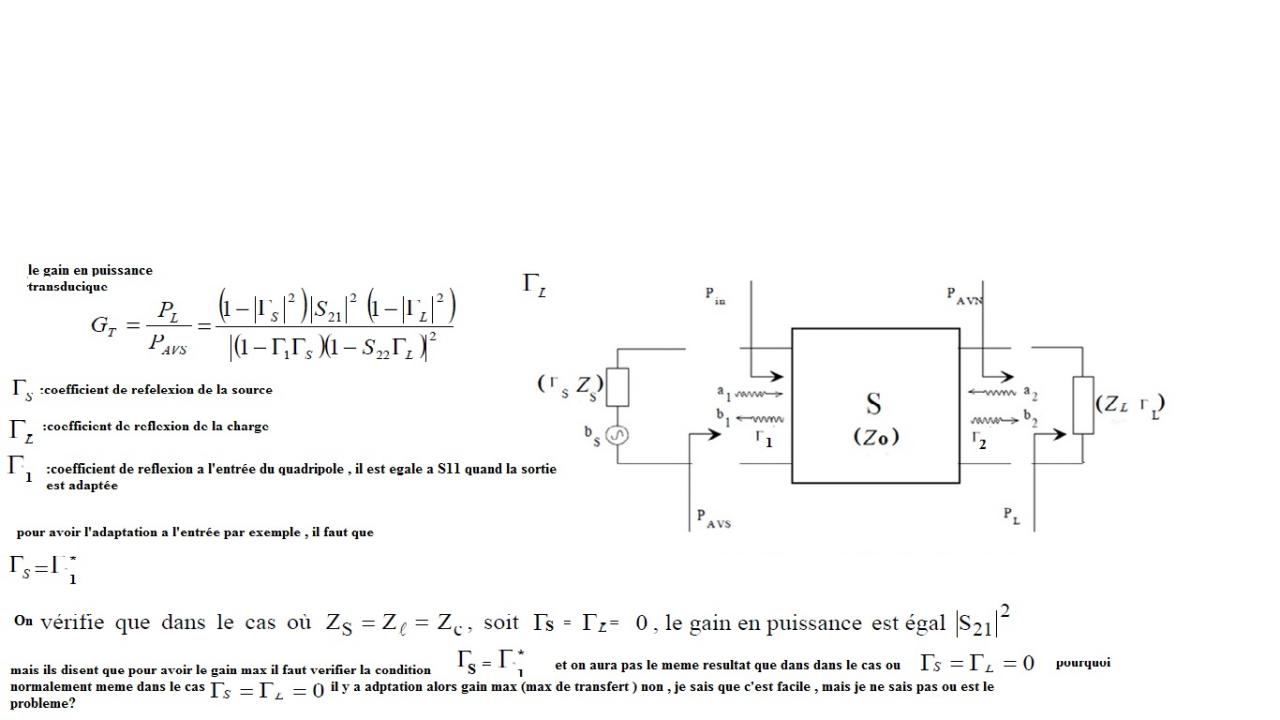
Pour rappel, le gain transducique, c'est le rapport de la puissance dissipée dans la charge branchée au quadripôle et de la puissance maximale possible de l'onde incidente(a) à l'entrée du quadripôle(ce qui nécessite que l'impédance du générateur soit adapté à l'impédance caractéristique de la ligne qui alimente le quadripôle). On voit que dans cette définition, le dénominateur dépend d'un cas de figure où le générateur est adapté à la ligne, ce qui est différent du cas de figure où l'on cherche à adapter l'impédance du générateur à l'impédance d'entrée du quadripôle(transfert maximal de puissance à l'entrée du quadripôle). Je pense que ton incompréhension vient de là.

[Abu Maria.]

ok merco b@
donc il y a une difference entre :
1-adapter par une ligne entre le generateur et le quadripole , le gain sera normalement egale a (module)

2- relier directement le generateur avec le quadripole et pour avoir l'adaptation il faut que z(generateur)=zin* , et dans ce cas le gain sera egale a une autre formule qui est differente de celle mentionnée en haut

dans les deux cas il y a une adaptation donc le transfert max de puissance

pourquoi on ne trouve pas les memes resultat du gain en puissance , pourquoi physiquement ?

[A voir en vidéo sur Futura]

[b@z66]

ok merco b@
donc il y a une difference entre :
1-adapter par une ligne entre le generateur et le quadripole , le gain sera normalement egale a (module)

Non, pas tout à fait. L'introduction de la notion de ligne dans ma précédente explication ne vient pas du fait qu'il y en ait réellement une mais du fait que les paramètres S du quadripôle (notamment les coefficients de réflexion S11et S22) sont déterminés à partir d'une impédance caractéristique de référence pour les accès à ce quadripôle: rien n'empêche de faire tendre les longueurs de ces lignes vers 0 et c'est ce qu'il se passe ici.

Le gain transducique valant S21s'explique très bien:l'onde incidente(sur une ligne hypothétique de l'impédance caractéristique considérée) à l'entrée du quadripôle se trouve multipliée par S21 en étant transmise à sa sortie. Ensuite, du fait que l'on considère un cas de figure où le coefficient de réflexion en sortie est nul, toute la puissance est donc absorbée par la charge. Comme le choix de l'impédance caractéristique de référence est arbitraire, le fait de poser gammaS et gammaL égal à 0 ne donne pas nécessairement une situation où le transfert de puissance est maximal, cela permet juste de constater que le gain que l'on obtient devient égal au S21 défini pour l'impédance caractéristique pour laquelle on a fait en sorte d'adapter entrée et sortie. Si on avait fait en sorte d'adapter entrée et sortie pour une autre impédance caractéristique, on aurait obtenu un autre gain qui aurait été égal au S21 défini pour cette autre impédance caractéristique.

2- relier directement le generateur avec le quadripole et pour avoir l'adaptation il faut que z(generateur)=zin* , et dans ce cas le gain sera egale a une autre formule qui est differente de celle mentionnée en haut

dans les deux cas il y a une adaptation donc le transfert max de puissance

pourquoi on ne trouve pas les memes resultat du gain en puissance , pourquoi physiquement ?

Dans le deuxième cas, on adapte effectivement de sorte que z(generateur)=zin*: on a ainsi, entre le générateur et l'entrée du quadripôle, un transfert de puissance maximal(sans réflexion "effective" de la puissance à l'entrée du quadripôle). Ton problème de compréhension avec le premier cas vient apparemment toujours de la présence de cette ligne "virtuelle" dont on fait tendre les longueurs vers 0. Je n'ai jamais moi-même vraiment compris l'intérêt de la définition du gain transducique(même si des raisons de symétrie dans la formule que l'on souhaite obtenir sont sans doute à prendre en compte) mais il diffère effectivement d'un gain normal(entre la puissance dissipée dans une charge et la puissance délivrée par un générateur) dans le sens où l'on divise la puissance dissipée par la charge par une puissance "théorique" maximale délivrée par l'ensemble du générateur (bs+Zs sur ton schéma) qui est égale à (1/2). R.Imax²=(1/2).Re(Zs).(bs/Re(Zs+Zin))²=(1/2).(bs²/4.Re(Z1)) puisque l'on y considère Zin adapté à Z1(Re signifiant partie réelle).

[b@z66]

Pour la définition du gain transducique, tu peux te rapporter à ce document également.

Pièce jointe supprimée.

[JPL]

Source non citée.

[Abu Maria.]

quoi que ce qu'il y a ?

[JPL]

Mon message s'adresse à b@z66, pas à toi. Son pdf est la photocopie de deux pages d'un livre non identifié.

[Abu Maria.]

je sais que c'est adressé a b@ mais j'ai repondu car je suis interessé par le pdf !
mais c bon je ne savais pas la raison de la non validation , maintenant je le connais
merci