calculs avec des rayons et des courbures

[invite9c7554e3]

Bonjour tous,

je vous écris car j'ai un petit soucis avec les courbures et des petits calculs associés. J'espère que vous pourrez m'éclairer un peu tous ceci

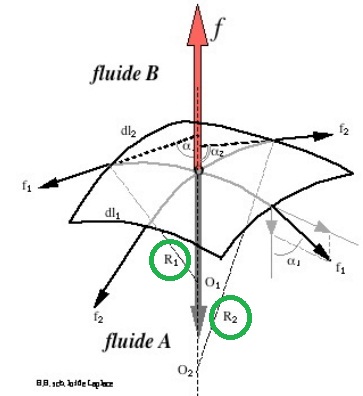
1°) mon premier soucis intervient dans la loi de laplace en mécanique des fluides (cf image en PJ) :



en gros on a une plaque rectangulaire dont le rayon de courbure des côtés est donnée par et et on sait que la différentielle de pression est donnée par (jusqu'à la pas de soucis j'ai tous compris).

=> par contre je n'ai pas compris pourquoi on dit que est la courbure moyenne :euh: j'aurais dit plutôt que c'est la courbure totale puisque par définition la courbure est .

=> je me suis dit que c'était une erreur dans ce cours mais le problème est que j'ai trouvé ceci presque partout o_O

=> au fait, j'ai une autre question en peux dans le même esprit : une sphère à une courbure de 1/R et une ellipsoide à donc deux courbures 1/R1 et 1/R2 mais si on veut donner une courbure moyenne pour l'ellipsoide ce sera la somme des courbures divisé par 2 ? es ce que ça veut dire que le rayon moyen et la somme des deux rayons divisé par deux aussi ?

2°) ma 2eme question est un peu plus compliqué :

=> pour une sphere de rayon je devais calculer la grandeur où et sont les incréments de surface et volumes engendrés par un incrément de rayon .
pour ceci j'ai trouvé la solution : car et

=> le soucis est que maintenant je dois faire la même chose mais pour un cylindre (R,L) et pour une ellipoide (R1,R2).

2-1) Pour le cylindre, j'ai un rayon initial et une longueur initiale et mon cylindre augmente de et . Je dois trouver le rapport D comme tout à l'heure mais si possible sans faire apparaitre les incrément et . Juste et .
=> je m'embrouille un peu les pinceaux du coup je ne suis pas certain que ce soit possible... peut être en faisant intervenir un parametre d'allongement (=longueur/rayon) en pensant n'avoir plus qu'une derivation a faire. Le soucis est que le facteur d'allongement depend aussi de R et L du coup sa ne simplifie rien? Ou peut etre que je devrais le considérer comme constant puisque mes dR et dL sont petits ???

2-2) pour l'ellipsoide mon probleme est le même, mon soucis vient du fait que je n'arrive pas à trouver l'expression de la surface de l'ellipsoide sur le net, je trouve des choses mais c'est pas très clair...
=> du coup peut être que je peux arriver à m'en sortir en faisant intervenir les deux courbures d'une ellipse ou une sorte de courbure moyenne ? En fait je remplacerai le 2/R du cas de la sphere par 1/R1 + 1/R2 mais je ne sais pas si cette hypothese est grossiere???

bref, je suis un peu pommé et j'espère que vous pourrez m'aider

je vous remercie d'avance
-----

[LPFR]

Bonjour.
Le premier point est une simple question de définition. On définit la courbure moyenne en ajoutant le ½. Regardez wikipedia.
Je suis bien d'accord que la courbure totale, sans le ½, est un concept plus satisfaisant.

Pour le second point, je pense que le problème est mal posé et qu'il ne s'agit pas d'une sphère, un cylindre ou un ellipsoïde, mais d'un "zeste" de sphère: une calotte sphérique. Et d'une calotte très petite, adapté au calcul différentiel.
Vous pouvez calculer la surface et le volume d'une calotte sphérique ou le trouver dans le web.
Bien sur, pour le cylindre, le plus petit "zeste" à une longueur infinie. Donc, il s'agit de faire le calcul pour une longueur quelconque, mais une largeur très petite.
L'ellipsoïde se déduit de la calotte sphérique et se souvenant que pour transformer un cercle en ellipse, il suffit de multiplier une direction par un coefficient.
Ainsi, si la surface d'un cercle est pi.a², celle d'une ellipse est pi.a.b. Mais c'est aussi valable pour la surface ou le volume d'une calotte.
Au revoir.

[phys4]

Bonjour,

Le but de l'exercice est visiblement de vous faire retrouver que la courbure totale d'une surface est la quantité D

Il ne faut donc pas utiliser la conclusion à priori.
Pour le cylindre, il faut prendre la longueur du cylindre comme une constante.

Vous trouverez tout sur l'ellipsoïde ici par exemple:
http://www.mathcurve.com/surfaces/el...llipsoid.shtml

Vous remarquerez que l'aire d'un ellipsoïde quelconque ne s’intègre pas. Je n'ai pas essayé de dériver l'intégrale ?

[invite9c7554e3]

en fait je n'ai pas précisé : les questions 1°) et 2°) sont totalement indépendantes ce n'est pas le même exercice, je les ai mis à coté car je me suis dis que je pouvais m'inspirer de l'exercice 1 pour résoudre des choses plus complexe de l'exercice 1. mais j'insiste, ils n'ont aucun liens et proviennent de deux cours différents.

sinon, pour répondre à ta question LPFR je dois bien calculer D pour une sphere, une ellipsoide et un cylindre

[A voir en vidéo sur Futura]