Équation de la chaleur ?

[invited9b9018b]

Bonsoir,

J'ai besoin pour un projet de "résoudre" l'équation de la chaleur. Il s'agit en fait d'une étude de l'effet Yarkovsky (http://fr.wikipedia.org/wiki/Effet_Yarkovsky)
J'ai déjà amassé bon nombre d'informations, et entamé une logiciel de simulation, qui calcule d'ores et déjà à partir d'un modèle 3D des caractéristiques intrinsèques d'un astéroïde. (matrice d'inertie, etc.).
La surface d'un astéroïde est découpé en faces élémentaires. (~ 12000 faces pour mon modèle de test, mais ce sera moins en pratique).
J'ai donc besoin de déterminer la distribution de température en surface de l'astéroïde à chaque instant.
Pour cela il faut résoudre l'équation de la chaleur. Je pensais donc le faire en 1D face par face (c'est d'ailleurs ce qui semble être le plus courant, d'après mes lectures).

Je me suis donc renseigné à ce sujet, j'ai collecté beaucoup de documents mais ce n'est pas évident de s'y retrouver, les approches étant très différentes.

Voici le problème tel qu'il est posé (pour une face donnée). On part donc de l'équation de la chaleur 1D (selon la profondeur) :



On se donne aussi une autre condition limite :


Où phi(t) est le flux solaire (W/m², nul lorsque la face est ombragée, égal au flux radiatif du soleil sinon), A l'albedo de bond et theta l'angle entre la normale à la face et la direction du soleil.

Certains se donnent également comme autre condition limite :


Où delta est la profondeur de pénétration de l'"onde thermique", où omega est la pulsation du phénomène étudié (diurnal ou saisonnier en fait).

N'ayant jamais véritablement étudié les équations aux dérivées partielles, je pensais d'abord faire une résolution exclusivement numérique. Mais une approche analytique / semi analytique permettrait de gagner en temps de calcul et serait aussi plus intéressante.

J'ai donc consulté bon nombre de documents mais cela reste assez flou pour moi. J'en ai parlé avec un prof qui par chance trouve le problème intéressant.
On a essayé plusieurs choses. La méthode de séparation des variables semblaient donner des résultats étranges. (par exemple, une distribution sinusoïdale des températures selon la profondeur z), et ne permettait pas de tenir compte simplement des conditions limites.

Supposer un régime sinusoïdal forcé (après tout, l'échauffement du soleil est en bonne approximation un demi sinus, d'amplitude et moyenne calculable facilement par rotation du corps sur une période) mais cela ne permettait pas de prendre en compte les pertes par rayonnements dans la condition limite de façon satisfaisante. (Même si grâce à ça j'ai compris l'origine de l'expression de delta par exemple donc ce n'était pas inutile )

J'ai également remarqué que si les pertes par rayonnement sont linéarisées (petites variations de température), cela ressemble un peu au problème de l'ailette... Mais je ne vois pas comment le résoudre dans le cas instationnaire ?

Au final, peut être vaut-il mieux opter pour une résolution numérique. Mais voilà : comment imposer des conditions limite dans le schéma numérique sans rendre la chose instable ? (fixer les dérivées spatiales aux bords fait diverger très vite le système ?!)

Bref vous l'aurez compris, le soucis vient de mon manque de connaissances sur la résolution d'une telle équation. Auriez vous des documents particuliers à me proposer, concernant une approche analytique ou numérique ? (ou les deux )
J'ai aussi vu plusieurs fois qu'il était fait mention d'une résolution par séparation des variables et utilisation des séries de fourier; Si vous aviez des explications à ce sujet également je serais très intéressé

Merci d'avance pour votre aide (et désolé pour ce post un peu long peut être).

Bonne soirée, A+
-----

[obi76]

Salut,
juste à titre de curiosité, ton maillage il est comment ? Régulier ?

Le problème est très intéressant, mais vu que ce sont des équa diff avec des termes qui montent jusqu'à la puissance 4, je doute qu'une solution analytique existe... Ou alors avec de sacré approximations (ou une solution imbuvable).

[invited9b9018b]

Re !

Merci pour votre réponse !

Salut,
juste à titre de curiosité, ton maillage il est comment ? Régulier ?

Oui, le découpage se fait de façon régulière sur une distance arbitraire

Le problème est très intéressant, mais vu que ce sont des équa diff avec des termes qui montent jusqu'à la puissance 4, je doute qu'une solution analytique existe... Ou alors avec de sacré approximations (ou une solution imbuvable).

On peut considérer des petites variations de température uniquement si nécessaire : et donc (Il semblerait que ce soit une bonne approximation dans de nombreux cas).

Merci encore, A+

[obi76]

Oui effectivement, si tu linéarises il y a peut être une solution analytique...

[A voir en vidéo sur Futura]

[invited9b9018b]

Bonjour,

Oui effectivement, si tu linéarises il y a peut être une solution analytique...

Oui, d'autant plus que le terme d'éclairement peut être calculé de façon préliminaire et c'est (en gros) un demi sinus (décale d'une constante en général)

A+

[invite34688568]

En fait, il y a peut-être moyen de simplifier en prenant la puissance du rayonnement par surface, appliquer une correction selon l'angle de la face observée.
(50 % sont à zéro et la frontière tend vers zéro tandis que les facettes face au soleil reçoivent quasiment 100% du rayonnement (calcul sur une fonction trigonométrique simple).

Une fois la puissance locale calculée, la traduire en puissance en l'appliquant à la surface observée (quoique l'on puisse le faire déjà avec l'étape précédente si l'on veut).
Ensuite prend l'émissivité du matériau de l'astéroïde ce qui donnera la quantité de rayonnement absorbée contre la quantité réfléchie.

Et enfin, la résistivité thermique du matériau de l'astéroïde permettra de déterminer la profondeur atteinte par le rayonnement, je suppose que l'on aurait le droit d'abusivement décréter qu'à part les faces éclairées, le reste de l'astéroïde est à peu près au zéro absolu?

[invited9b9018b]

Merci pour votre réponse
Mais je pense que cette partie là (qui revient en fait à définir les conditions aux limite) est déjà résolue. Le calcul de l'éclairement d'une face sur une période est même possible de façon préalable, et conduit à une puissance reçue de la forme :



Du coup je pensais exploiter la linéarité de l'équation pour superposer des solutions. Je pourrais éventuellement décomposer Phi en série de fourier et superposer les solutions sinusoïdales forcées. Puis ajouter la solution correspondant à la perte par rayonnement seule. Mais ce n'est pas la façon dont sont exploitées les séries de fourier en général pour résoudre ce problème si j'ai bien compris et surtout, je ne suis pas sur que je puisse additionner la solution correspondant à l'éclairement seul et la solution correspondant aux pertes seules, car elles ne me semblent pas vraiment indépendantes (la perte est une fonction de la température !)

A+

[obi76]

Re,

c'est exactement ce à quoi j'avais pensé hier : pour l'énergie reçue, c'est nécessairement défini par morceau. Cela dit, c'est infiniment dérivable.

Je présume qu'avec une condition initiale (en température) quelconque, l'évolution de la température va converger vers une solution periodique. En trouvant la solution du côté où l'énergie reçue est nulle et en posant une condition avec celle quand le côté est exposé à la lumière solaire, il y a peut être moyen de sortir quelque chose...

[invite34688568]

Le problème c'est qu'en choisissant un astéroïde, il ne simplifie pas vraiment l'équation puisque l'émissivité d'une surface dépend de sa nature, de sa texture mais aussi de la géométrie.
Ainsi, si il y a des cavités un peut profonde (genre 1/5 à 17/7 de diamètre vis à vis de la profondeur), on pourrait arriver à une émissivité de quasi corps noir sur certaines surface et influer en prime sur la profondeur de rayonnement.

Mais oui, hélas, tu as totalement raison, au pire on fait une moyenne de la nature de la surface (ce qui reste une approximation) mais, en théorie on arrive jamais au bout à cause des effets des surfaces entre elles (elles peuvent recevoir le rayonnement réfléchi de leur voisine et inversement) puisque c'est un corps réputé irrégulier.

[obi76]

Avant de partir dans des détails comme ceux-là, c'est sans doute mieux de simplifier pour essayer de trouver une solution analytique et éventuellement les confronter à un simulation...

On peut faire plus simple : vous avez déjà vu un astéroïde parfaitement sphérique vous ?

[invited9b9018b]

Re !

Re,

c'est exactement ce à quoi j'avais pensé hier : pour l'énergie reçue, c'est nécessairement défini par morceau. Cela dit, c'est infiniment dérivable.

Je présume qu'avec une condition initiale (en température) quelconque, l'évolution de la température va converger vers une solution periodique. En trouvant la solution du côté où l'énergie reçue est nulle et en posant une condition avec celle quand le côté est exposé à la lumière solaire, il y a peut être moyen de sortir quelque chose...

Merci pour vos réponses !

En fait je ne suis pas sur de ce qu'il faut faire :
1) faire une disjonction de cas, ça revient à considérer des phénomènes transitoires de façon alternative (jour/nuit/...). La nuit on aurait une décroissance exponentielle, et le jour s'ajouterait une sorte d'impulsion en demi sinus et donnerait une solution dont je ne suis pas certain de la forme
2) supposer un régime permanent périodique mais un peu compliqué dont je n'ai pas trop d'idée de la forme.


En fait, il est peut être mieux de commencer par une résolution numérique précise sur une face (indépendamment de l'étude des autres effets). Le but étant de connaitre l'allure de la solution à prévoir. Puisqu'on travaille sur une seule face "pour voir", on se fiche des performances et on peut faire quelque chose d'assez précis.
Dans ce cas en procédant par différences finies, donc en discrétisation l'équation de la chaleur :



Et ce sur une distance finie.

Cependant pour appliquer les conditions limite, ça se complique. Par exemple, en z = 0 (surface), forcer (où f est la condition limite en surface donnée plus haut) est assez douteux et fait diverger immédiatement le modèle.
(En fait cela se traduit par des variations énormes sur les bords, en gros graphiquement comme sur les graphes représentant le phénomène de gibbs sur un créneau )

Le problème c'est qu'en choisissant un astéroïde, il ne simplifie pas vraiment l'équation puisque l'émissivité d'une surface dépend de sa nature, de sa texture mais aussi de la géométrie.
Ainsi, si il y a des cavités un peut profonde (genre 1/5 à 17/7 de diamètre vis à vis de la profondeur), on pourrait arriver à une émissivité de quasi corps noir sur certaines surface et influer en prime sur la profondeur de rayonnement.

Mais oui, hélas, tu as totalement raison, au pire on fait une moyenne de la nature de la surface (ce qui reste une approximation) mais, en théorie on arrive jamais au bout à cause des effets des surfaces entre elles (elles peuvent recevoir le rayonnement réfléchi de leur voisine et inversement) puisque c'est un corps réputé irrégulier.

J'avais déjà considéré ces problèmes et j'ai choisi de les négliger. L'objectif ici est surtout de proposer une méthode peut être un peu simpliste mais en tout cas illustrant le principe de la simulation.
Des simulations existantes prennent effectivement en compte des paramètres tels que l'état de surface et les réflexions/réémissions d'une face à l'autre mais je me suis restreint aux formes d'astéroïdes relativement convexes (ne serait-ce que pour la tétraédrisation et le calcul de la matrice d'inertie) donc je ne fais pas vraiment d'"hypothèse supplémentaire" en faisant ce choix.

Merci et a+ !

EDIT: je viens de repérer une coquille dans le premier poste, dans la CL en profondeur, il faut lire et pas , désolé :s

[invite34688568]

En fait, tu pourrais modéliser des échantillons et les tourner en simulation.
Après, tu fais une projection statistique des cas modélisés (plane, rugueux, monticule, cratère, creux, ...)
De toute façon aussi, dès 60° pour l'incidence, l'émissivité chute tellement que tu peux négliger aussi une grande partie de ce côté-là.
Je suppose que l'on n'a pas de résultats de températures pris par une sonde posée sur un astéroïde ou un planétoïde sans atmosphère pour avoir un exemple réel?

Je demande, vu que tu veux étudier l'effet Yarkovsky, si tu ne devrais pas plus t'orienter sur l'angle limite à partir duquel l'astéroïde commence à réémettre le rayonnement et l'angle théorique, fonction de sa rotation, à partir duquel il a dissipé toute l'énergie.
Je ne suis pas certain que tu doives étudier tout l'astéroïde mais seulement les parties à partir desquels il s'échauffe et celles où il refroidit, tu pourrais finalement ignorer presque 50% de ton astéroïde voire plus, l'angle de réchauffement "utile" n'étant finalement pas très grand.
Le reste, finalement est à l'équilibre et vu les extrêmes en présence, il y a fort à parier que le refroidissement soit très rapide.
De combien le soleil réussit-il à réchauffer une face visible d'astéroïde à hauteur de la ceinture d'astéroïde?

[invited9b9018b]

Re !

@hcrepin: s'il existe des données expérimentales assez précises concernant la distribution et l'évolution de la température en surface d'un astéroïde, je ne les ai pas trouvées.
Je ne suis pas certain d'avoir parfaitement saisi votre message, mais il me semble que ce sont des simplifications qui ne permettront pas vraiment de résoudre le problème de la température. Une fois la solution trouvée pour la température, avec des modèles 3D simples (peu de faces), il sera mieux de considérer l'astéroïde en sa totalité à chaque instant.


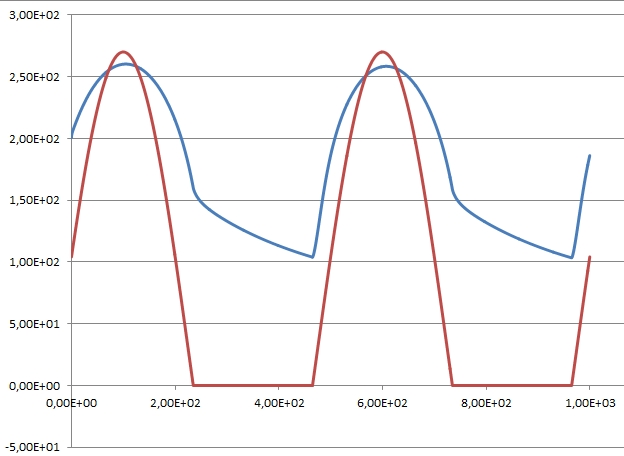
A part ça, j'ai avancé J'ai réussi à faire un calcul numérique correct et plutôt réaliste pour prévoir la forme de la solution.
J'ai pris pour cela un bloc de granit (parce que j'avais des valeurs de conductivité/diffusivité pour ce matériau ) situé à 2 UA du soleil environ, avec une période de rotation (diurne) de 1000 s. J'ai utilisé la méthode des différences finies décrite plus avec comme CL en surface : .
En fait le premier modèle était instable parce que le pas de temps était trop court (il faut apparemment qu'il respecte certaines conditions, par exemple il doit être d'autant plus petit que le pas spatial est petit).

Voici le résultat :



(http://sciencestechniques.fr/asteroids/temperature1.jpg)

En bleu : la température de surface, en K (échelle en ordonnée)
En rouge : la puissance reçue depuis le Soleil (en W/m², même échelle que la température)
En abscisse : le temps (en s).

Conclusions :

• Déjà, la linéarisation de T⁴ dont j'avais fait mention semble une mauvaise idée, vu l'importance des variations.
• Cela dépend peut être de la période, des caractéristiques thermiques du matériau, mais il semble que le déphasage entre le pic du température et le pic d'éclairement soit quasi nul
• lorsqu'il y a éclairement, la forme de T est plus ou moins semblable a une sinusoïde, mais il résulte une hausse de la température à la fin d'une "journée", je ne vois pas trop comment traduire ça mathématiquement
• la "nuit", lorsqu'il n'y a que refroidissement, la courbe parait assez linéaire mais c'est un hasard (je men suis rendu compte en changeant quelques valeurs). En réalité cela ressemble plus à une décroissance exponentielle (mais pas tout à fait, à cause de l'inertie thermique ?)

Je vais voir ce que ça donne "spatialement" (à t fixé déjà). Je vais aussi changer le cos theta max (en regardant ce qui se passe près des pôles par exemple).

A+

[invite34688568]

J'ai un problème avec ton "départ", je ne comprends pas comment il est aussi brutal alors que l'on vient de l'angle limite.
Et je crois que tu devrais choisir un exemple avec un palier nocturne sinon tu risques de te faire coincer sur l'aspect qu'il pourrait y avoir accumulation d'énergie puisqu'elle n'a pas le temps d'être évacuée durant la période "nocturne".

Le refroidissement nocturne peut très bien être linéaire puisque les conditions extérieures y sont stables ce qui n'est pas le cas de la partie diurne et d'une efficacité progressive et il n'y a pas de changement d'état.

[invited9b9018b]

J'ai un problème avec ton "départ", je ne comprends pas comment il est aussi brutal alors que l'on vient de l'angle limite.

Je viens de chercher si on pouvait trouver des courbes similaires sur le net, c'est le cas :

http://ars.els-cdn.com/content/image...000553-gr6.jpg
Où encore en bas de cette page: http://www.climat-evolution.com/article-21572753.html
Bref j'ai confiance en mes résultats

Et je crois que tu devrais choisir un exemple avec un palier nocturne sinon tu risques de te faire coincer sur l'aspect qu'il pourrait y avoir accumulation d'énergie puisqu'elle n'a pas le temps d'être évacuée durant la période "nocturne".

Le refroidissement nocturne peut très bien être linéaire puisque les conditions extérieures y sont stables ce qui n'est pas le cas de la partie diurne et d'une efficacité progressive et il n'y a pas de changement d'état.

Je ne suis pas sur de bien saisir ce que vous essayez de dire... "Palier nocturne" ?
Aussi le refroidissement n'est pas linéaire, surtout vu les variations de température ! (Bon après l'inertie thermique est faible dans cet exemple).

A+

[Gilgamesh]

Hello,

Je tombe sur cette discution et ça rejoint un peu mon problème de calcul thermique sur mon arche interstellaire. Dans ce cas j'ai un tube (on va dire infiniment long) avec de l'eau en circulation qui refroidit en rayonnant dans le vide. La question est de savoir au bout de quelle longueur l'eau passera en dessous d'une certaine température (disons 4°C) en fonction du diamètre intérieur du tube, de son épaisseur de sa conductivité thermique et de la vitesse de l'eau.

Je suis jamais arrivé à dépatouiller la chose (notamment évidemment à cause du facteur T4)

Juste au cas où... Vu que tu est "chaud" sur le sujet, lucas, et nettement plus doué en math que moi, est ce que tu aurais les éléments de calcul sous la main pour effectuer une estimation en fonction des paramètres d'entrée ?

Merci.

[invited9b9018b]

Bonsoir,

J'ai regardé ça, c'est intéressant je vous envoie un message privé dans les minutes qui viennent pour vous envoyer ce que j'ai trouvé.
Faut-il prendre en compte un rayonnement extérieur (source de chaleur) ?

A+

PS: n'exagérez pas quant à mes capacités

[obi76]

Re,

disons que si les conditions initiales sont définies par morceau, il y a fort à parier que les solutions aussi...

[obi76]

PS :

J'ai un problème avec ton "départ", je ne comprends pas comment il est aussi brutal alors que l'on vient de l'angle limite.

là je suis d'accord, ce n'est pas dérivable lorsqu'un morceau passe à l'ombre sur ton graphique... Le flux d'énergie reçue doit être est maxi lorsque la source est normale à la surface, et va descendre à lorsqu'elle est perpendiculaire (si la source est ponctuelle)... Intuitivement je dirai que la source DOIT être sans discontinuité...

[invited9b9018b]

Bonsoir,

PS :
là je suis d'accord, ce n'est pas dérivable lorsqu'un morceau passe à l'ombre sur ton graphique... Le flux d'énergie reçue doit être est maxi lorsque la source est normale à la surface, et va descendre à lorsqu'elle est perpendiculaire (si la source est ponctuelle)... Intuitivement je dirai que la source DOIT être sans discontinuité...

Mais c'est bien le cas ? La courbe d'éclairement est continue, elle n'est juste pas , ce qui me parait correct ?

A+

[obi76]

La courbe d'éclairement est continue, elle n'est juste pas , ce qui me parait correct ?

Je dirai qu'elle est effectivement (après réflexion, tu as raison, elle n'est pas infiniment dérivable). Cela dit sur ta courbe, là où hcrepin et moi sommes d'accords, c'est qu'elle est .

[invite34688568]

J'ai finalement compris en reprenant un peu les calculs, c'est à cause des échelles de temps qui sont très serrées donc c'est tout à fait plausible que le départ soit aussi raide

Quand je parle de palier, je parle de choisir un exemple où la rotation amène à une décharge totale de l'énergie accumulée et donc va avoir une courte phase de température totalement stable avant de reprendre.
Sinon, si l'énergie n'est pas complètement dissipée, tu pourrais avoir un phénomène où l'astéroïde stocke la chaleur jusqu'à une valeur d'équilibre et ça compliquerait méchamment ton modèle.

En tous les cas, c'est vraiment un beau projet.

[invited9b9018b]

Bonsoir,

Je vais essayer de faire des graphes 3D de T(z,t) demain

A+

[invited9b9018b]

Chose promise, chose due.

J'ai changé les valeurs d'inertie thermique (j'avais laissé des valeurs incorrectes pour amplifier les variations).

Voilà maintenant avec une période de 10 h (approx)

c26526b14447e991a289b4a842a63d8eecbc4147.jpg

2b3b61a635de89e3f8028e4062e97e15ad52fa6e.jpg

1792cd5b291a14a5db5813ffe94194060643df70.jpg

Voilà, je pense pouvoir me débrouiller avec ça (soit en faisant tout numériquement, soit en tentant une approche analytique tenant compte de ces résultats).


A+