Bonjour,
L’objet du poste est de lever le voile sur certaines zones d’ombres liées au paradoxe des jumeaux posé par Paul Langevin il y’a plus d’un siècle.
Si vous êtes déjà familier à la théorie de la relativité ou au paradoxe présenté je vous invite à lire directement la partie V.
I- Présentation du problème :
Fixe et Mobile sont les prénoms de deux frères jumeaux. Ils habitent la planète Galileo, isolée dans l’Univers, et dont on peut supposer que la surface définit un référentiel galiléen.
Tandis que Fixe reste sur Galileo, son frère Mobile, lui, monte à bord d’un véhicule qui se déplace à une vitesse, notée v=2,6 x 10^8 m.s^-1 . Pendant 7 années, il s’éloigne de Galileo.
Pendant les 7 années suivantes, il revient voir son frère. Ces durées sont celles mesurées par Mobile.
Problème : Au retour de Mobile, lequel es deux frères est le plus âgé ?
Mobile dit :
« Je suis en mouvement à très grande vitesse par rapport à mon frère : le facteur de Lorentz vaut environ 2. Donc en vertu de la dilatation des durées, pendant que ma pendule effectue un tour, la sienne en effectue 2. Ainsi, à mon retour, mon frère sera deux fois plus vieux que moi ! »
Mais Fixe répond :
« Je ne suis pas d’accord ! On peut très bien considérer que c’est moi qui suis en mouvement à la vitesse v par rapport à mon frère ! Donc de mon point de vue, c’est la durée mesurée par lui qui est dilatée ! Et donc pendant que ma pendule effectue un tour la sienne en effectue deux, c’est donc lui qui reviendra deux fois plus âgé que moi ! »
II- Quelques définitions et notions liées au cours :
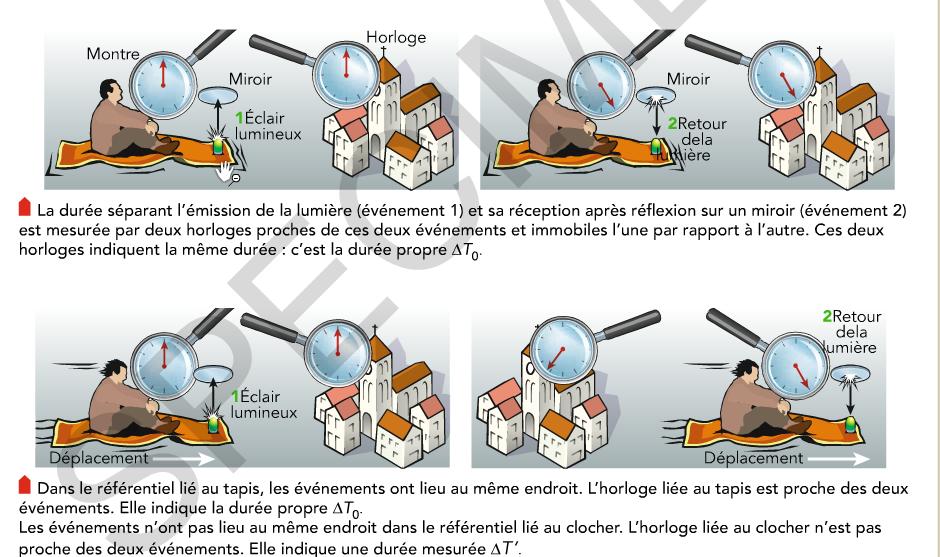
« -Le temps propre, ou durée propre, ∆T est la durée séparant deux événements ayant lieu au même endroit dans un référentiel galiléen (R ). Cette durée est mesurée par une horloge fixe dans ce référentiel (R ) et proche des deux évènements.
-Le temps mesuré, ou durée mesuré, ∆T’ est la durée séparant deux évènements mesurée dans un référentiel galiléen (R’) en mouvement par rapport au référentiel galiléen (R ) dans lequel on mesure le temps propre. L’horloge qui mesure ∆T’ est fixe dans R’. »
Extrait du livre.
« -La durée impropre* est mesurée par une horloge liée à un référentiel galiléen
-Le référentiel propre est en mouvement à une vitesse constante par rapport au référentiel impropre. »
Extrait de l’énoncé du problème
* Par rapport à la définition du livre, il doit s’agir de la durée mesurée ∆T’.
III- Illustration par un exemple simple :
IV- Retour au problème posé :
.
Il me semble qu’il est important avant de répondre à la question de présenter dans cette situation les différents référentiels :
Fixe mesure le temps sur une horloge fixe dans un référentiel galiléen.
Mobile mesure le temps sur un vaisseau en déplacement à vitesse constante.
Les deux référentiels sont en déplacements relatifs, à ce stade là, on peut donc tout aussi bien considérer que ∆T’ est mesuré sur le vaisseau que sur la planète, c’est d’ailleurs tout l’objet du paradoxe.
La difficulté du problème est donc de pouvoir déterminer avec rigueur quel est le référentiel ou le temps propre est mesuré. Une fois établi, il devient alors simple d’appliquer les lois d’Einstein, et de reconnaître qui sera plus vieux.
En ce point les questions posées par l’énoncé nous amène à reconsidérer la trajectoire du vaisseau qui fait un aller retour :
Un aller retour suppose une modification de la courbe de la trajectoire, qui n’est plus alors parfaitement rectiligne, et même en supposant que la vitesse du vaisseau ne varie pas lors de la rotation, on ne peut plus alors le décrire comme étant un Référentiel proprement galiléen.
Si l’on s’arrête aux points de cours apportés par l’énoncé exclusivement, (cf en haut) on peut alors conclure sur le paradoxe en affirmant :
1° La trajectoire du vaisseau n’est pas rectiligne.
2° D’après le principe d’inertie newtonien, le vaisseau ne définit pas un référentiel galiléen.
3° La durée impropre ou durée mesurée ∆T’ étant définie sur un référentiel galiléen, elle ne peut donc être déterminée que sur la planète Galileo.
4° Ainsi en vertu, de la relation ∆T’ = ∆T / √(1 – v²/c²) soit ∆T’= ∆T / 2 car le facteur de Lorentz est dit proche de 2 dans cet exercice.
5° Le temps ∆T’ s’écoulant 2 fois plus lentement sur Galileo que sur le vaisseau, on peut donc selon la logique des questions posées par l’énoncé dire : Fixe est plus jeune que Mobile au retour de ce dernier.
V- Le paradoxe dans le paradoxe :
Seulement voilà, en reconsidérant l’exercice à partir de la définition du livre, il m’est apparu une grosse incohérence :
Si vous reprenez les définitions, extraites du livre, présentées plus haut (II), vous remarquerez que durée propre et durée impropre ou mesurée sont toutes deux définies sur des référentiels galiléens !!
Ainsi le raisonnement mené précédemment ne tient plus car le point n°2 remet tout en question :
Si le vaisseau ne peut plus être considéré comme un référentiel galiléen ce qui est vrai au vu de la trajectoire qu’il effectue, alors on ne peut pas non plus parler de temps propre ∆T sur le vaisseau puisque celui-ci également doit être mesuré sur un référentiel galiléen ce qui ne semble pas être le cas !
Qu’en pensez vous ? Pourriez vous m’aider à lever le voile sur ce problème ?
D’avance un GRAND merci à tous les participants,
Et bonne fin de journée (soirée) .
-----




 ->
-> 
