Dérivée d'une courbe

[Fisikafon]

Bonsoir à tous !
Je suis actuellement en Première S, et la question de la dérivée vient d'être abordée en physique.
Je suis un peu (voire beaucoup) perdue quant à ce vaste sujet, et j'espère trouver des réponses sur ce forum.
En gros on a étudié le principe de Fermat (je ne saurais même pas le définir !)...
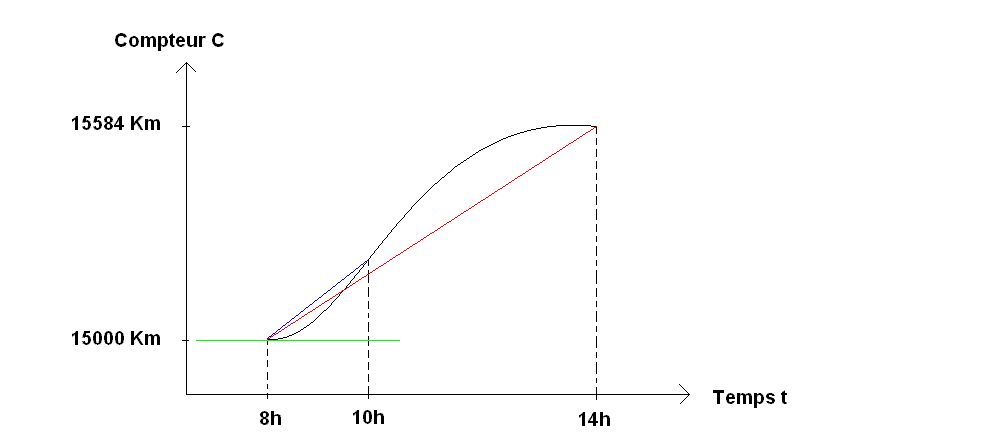
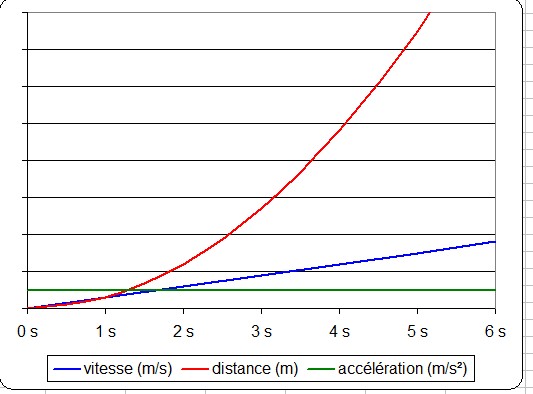
Donc si j'ai bien compris, la dérivée représente le taux de variation de deux points de la courbe...Et si xo tend vers 0 (que les deux points sont rapprochés) on obtient alors la tangente. Et la tangente en physique possède une unité qui est je crois m/s.
Déjà à ce stade je ne comprends pas vraiment pourquoi on fait cela.
Puis ensuite il y a une histoire de tangente = 0, qui représenterait un extremum de la fonction..
Et là je ne comprends vraiment plus grand chose.
Pourriez vous m'aider s'il vous plait ?
Merci d'avance !
-----

[Duke Alchemist]

Bonjour.

Déjà je suis surpris que vous abordiez le principe de Fermat en 1ère S mais bon.
Celui-ci dit (en simplifiant) que la lumière se propage en suivant non pas le chemin le plus court (en distance) comme on pourrait le penser mais le chemin le plus rapide : c'est donc un extremum en terme de vitesse et non pas la variable distance. En toute rigueur, c'est un extremum qui peut être un maximum ou un minimum.

N.B. : Ce n'est pas très rigoureux mais c'est pour que tu essaies de visualiser...
Est-ce que tu comprends ?

Revenons-en à nos dérivées
Tout d'abord, on parle de dérivée d'une fonction et non pas de dérivée d'une courbe.
La dérivée représente, comme tu l'as indiqué, le taux de variation d'une fonction pour deux abscisses très proches (donc de deux points de la courbe très proches) et si tu relies ces points très proche, et si ces points sont tellement proches que tu pourrais les confondre, tu constates que tu traces la tangente à la courbe en ce "double point"...
La dérivée correspond à la pente de ladite tangente. Tu le verras en maths cette année.
Maintenant, si la fonction admet un extremum (maximum ou minimum) alors la tangente en ce point est horizontale donc de pente nulle : la dérivée est nulle en ce point.

Et la tangente en physique possède une unité qui est je crois m/s.

La dérivée possède une unité mais pas la tangente qui est une droite.
La dérivée est en m/s si tu représentes la fonction distance (en m) en fonction du temps (en s).
Si on revient à la définition de la vitesse moyenne, c'est bien v = d/t ; la vitesse instantanée (c'est-à-dire à un à instant donné) est la dérivée de la distance suivant le temps. Les deux s'exprime en m/s.
Pour faire simple, dans ton cas, la valeur de la vitesse à un instant donné correspond à la pente de la tangente à la courbe représentative de la distance en fonction du temps.

Duke.

[gondebaud]

Bonjour,

Quand même bien dommage que vous voyez la notion du nombre dérivé maintenant avant le chapitre qui est prévu en maths, car là ça oblige à comprendre la notion de dérivation de façon anticipée.
Bon, d'un autre côté vous saurez à quoi peut servir la dérivation d'une fonction lorsque vous serez sur le chapitre du nombre dérivé en Mathématiques.

Sinon, de même que Duke Alchemist : Le nombre dérivé, que l'on note f'(a), d'une fonction dérivable f en un nombre a, est le coefficient directeur (ou la pente) de la tangente à la courbe représentative de f au point (a ; f(a) ).
Vous verrez une définition plus précise dans le chapitre en Mathématiques (et pas que ça) qui résumera ce que votre professeur de Physique vous a expliqué : En traçant une droite (MM0), M et M0 étant sur la courbe, puis en rapprochant M de M0 de plus en plus jusqu'à obtenir la tangente en M0. C'est une bonne approche pour comprendre.
ici, la fonction est x(t) (distance par rapport au temps). le nombre dérivée en t0 est alors la vitesse v0 à l'instant t0 et c'est le coefficient directeur (ou la pente) de la tangente à la courbe en t0.
Lorsque le nombre dérivée est égal à 0, la vitesse est alors nulle, la tangente à une pente nulle et est parallèle à l'axe des abscisses.

Cordialement.

[Fisikafon]

Merci beaucoup ! C'est bien plus clair dans mon esprit.
Oui, notre prof nous a dit que c'était une manière un peu spéciale que d'aborder la dérivée en physique...mais qu'il en avait besoin pour certaines choses.
Donc si je comprends bien, le calcul de la dérivée correspondrait à une simple lecture graphique ? Par exemple, pour la vitesse instantanée on lirait l'image d'un instant donné pour avoir la vitesse à cet instant, et pour le calcul de la dérivée dont la pente est nulle, c'est une lecture d'extremum (est ce qu'il est possible de calculer l'extremum avec -B/2a ?).
Mais étant donné que les deux seules informations dont on dispose sont les coordonnées des deux points, on est obligés de passer par la dérivée, c'est ça ?
Sinon il y a encore la notion de limite que je n'ai pas bien comprise, que cela représente-t'il ?
Et pour finir, quel est le rapport de la dérivée avec le principe de fermat ?
Je suis consciente que ça fait beaucoup de questions, mais je n'aime pas ne pas comprendre quelque chose. x)
Merci d'avance !

[A voir en vidéo sur Futura]

[gondebaud]

Par exemple, pour la vitesse instantanée on lirait l'image d'un instant donné pour avoir la vitesse à cet instant

Il suffit de lire le coefficient directeur (ou pente) de la tangente pour 'lire' la vitesse instantanée, oui.
Le coefficient directeur d'une droite a été étudié depuis la 3ème (voir 4ème) : on avance de 1 unité horizontalement et on regarde de combien d'unités on 'monte' ou de combien on 'descend' verticalement pour rejoindre la droite en question.

et pour le calcul de la dérivée dont la pente est nulle, c'est une lecture d'extremum

Si la courbe présente un extrémum en un nombre x0, la pente au point (x0; f(x0) est nul (et dans votre cas, la vitesse nulle). La réciproque n'est pas toujours vraie, on peut se retrouver avec un point d'inflexion (la courbe tend à avoir une tangente horizontale en (x0; f(x0)) à gauche en y restant "en dessous" puis à droite en étant "au-dessus" de la tangente, et dans ce cas f(x0) n'est ni un maximum ni un minimum).

Je n'ai pas compris le -B/2a ...

Mais étant donné que les deux seules informations dont on dispose sont les coordonnées des deux points, on est obligés de passer par la dérivée, c'est ça ?
Sinon il y a encore la notion de limite que je n'ai pas bien comprise, que cela représente-t'il ?

Deux points fixes ne suffiront pas à déterminer la dérivée, il faut imaginer que l'un des deux points se rapproche de l'autre "le plus possible", c'est par cela que l'on entend par limite (en gros : essayer d'obtenir quelque chose en s'en approchant le plus possible sans jamais l'atteindre).

Pour le principe de Fermat, je ne sais pas .

En espérant vous avoir éclairé,
A+

[interferences]

Bonjour,

Imagine un train, qui part à 8h () de la gare de Bordeaux et arrive à 14h () en gare d'Austerlitz.
Le compteur du train affichait 15 000 km à 8h ce matin et cet après midi (14h) il affiche 15 584 km.
Trouvez la vitesse moyenne du train.

Pour un problème comme celui là que fait-on comme calcul.
On peut présenter le calcul de cette façon :




Une autre question est maintenant de se demander si on ne peut pas avoir grâce à l'expression précédente la vitesse instantanée au départ du train.

Imaginons qu'on fasse varier le h dans l'expression précédente.
On n'aura plus :



Mais :



On voit bien que c'est le calcul de la vitesse moyenne du train sur les 2 premières heures du trajet.
Et maintenant, que se passe t-il quand on fait tendre h vers 0. On va obtenir la vitesse moyenne sur les premier instant du départ : la vitesse instantanée au départ du train.



Ou C'(t) est appelée dérivée par rapport au temps de C.



La vitesse c'est la distance parcourue divisée par le temps de parcours : C'est bien le coefficient directeur des droites tracées.

Au revoir

PS : On voit que le coefficient directeur de la courbe verte est nul, donc la vitesse instantanée est nulle. Ce qui paraît normal car le train part à l'arrêt et a une certaine inertie

[Duke Alchemist]

Rebonjour.

Oui, notre prof nous a dit que c'était une manière un peu spéciale que d'aborder la dérivée en physique...mais qu'il en avait besoin pour certaines choses.

Il a bien raison : la physique se "mathématise" de plus en plus dans le sens où on modélise de plus en plus les phénomènes par le biais d'équation (de degré divers). Il faut donc conserver un niveau correct en mathématique pour continuer en physique...

Donc si je comprends bien, le calcul de la dérivée correspondrait à une simple lecture graphique ? Par exemple, pour la vitesse instantanée on lirait l'image d'un instant donné pour avoir la vitesse à cet instant,...

Pour cela, il te faut la représentation graphique de la position en fonction du temps, sinon cela n'a pas trop d'intérêt en soi...

et pour le calcul de la dérivée dont la pente est nulle, c'est une lecture d'extremum (est ce qu'il est possible de calculer l'extremum avec -B/2a ?).

Oui. Le "-b/(2a)" n'est valable que pour les paraboles c'est-à-dire les équations du second degré.
@ gondebaud : Fisikafon faisait référence à l'étude des polynômes du second degré f(x) = ax²+bx+c pour le quel l'extremum se situe en -b/(2a) abscisse du sommet

Mais étant donné que les deux seules informations dont on dispose sont les coordonnées des deux points, on est obligés de passer par la dérivée, c'est ça ?

... Je ne suis pas sûr de bien comprendre ce que tu veux dire... Les exercices peuvent être présentés de manières tellement diverses qu'il est difficile de dire comme ça quelle méthode utiliser...
Détaille-nous cet exercice afin de voir comment "réagir" face à celui-ci.

Sinon il y a encore la notion de limite que je n'ai pas bien comprise, que cela représente-t-il ?

La limite, comme gondebaud l'a indiqué, correspond à une valeur (quand elle existe) vers laquelle tend une grandeur (qui peut être représentée par une fonction) sans jamais l'atteindre.
Un exemple simple : la fonction inverse f(x) = 1/x pour laquelle, quand x devient très grand, 1/x devient très petit et se rapproche de 0 sans jamais l'atteindre : 0 est donc la limite de la fonction 1/x quand x tend vers l'infini.
Bon, cela concerne plus les mathématiques que la physique. Je te propose donc de jeter un œil dans le forum mathématique (du collège et lycée) dans lequel, tu dois trouver des questions similaires en effectuant une recherche ou rouvrir une discussion.

Et pour finir, quel est le rapport de la dérivée avec le principe de Fermat ?

N'as-tu pas fait le lien entre le début de mon premier message ici et la suite de ce même message ??... Relis-le, je suis sûr que tu vas comprendre

Duke.

EDIT : @ interferences : Fisikafon n'a pas encore vraiment abordé les notions de limite de fonction et de dérivée et ton message pourrait sembler être hors de portée... mais je me trompe peut-être ...

[calculair]

Bonjour

La dérivée c'est la vitesse de variation de l'ordonnée par rapport à l'abscisse

La dérivée c'est aussi la pente de ma courbe en un point donné

La dérivée 'est la tangente à lza courbe en un point donné

la dérivée c'est donc (Xb - Xa )/( Yb - Ya) quand les point B et A sont très proches et on écrit parfois ( souvent ) dX /dY

Exemple quand tu freines , la derivée de la vitesse , c'est la vitesse de variation de la vitesse.....

[Duke Alchemist]

Re-

...
Exemple quand tu freines , la derivée de la vitesse , c'est la vitesse de variation de la vitesse.....

Ce qu'on appelle aussi l'accélération (ou la décélération ici)

Je précise cela pour Fisikafon, pas pour toi calculair

Duke.

[doul11]

Bonjour,

Et pour finir, quel est le rapport de la dérivée avec le principe de fermat ?

C'est pour trouver la solution du problème d'optimisation de temps de parcours : par exemple je marche sur un chemin et je doit rejoindre lieu dans un champ, je marche plus vite sur le chemin que dans le champ, la question est donc de savoir a quel moment je doit quitter le chemin pour passer a travers le champ ? Si on trace la courbe du temps de parcours en fonction du point ou je quitte le chemin on obtient un sorte de parabole, le temps le plus court est en bas du creux, pour trouver ou se situe exactement le temps le plus court on va calculer la dérivé de la courbe et regarder la ou elle vaut zéro.

Pour bien visualiser tout ceci je te conseille vivement de faire des dessins.

[albanxiii]

Bonjour,

Une petite remarque de vocabulaire : on ne dérive pas un courbe, on dérive une fonction (dont on a éventuellement tracé la courbe représentative). Et la dérivée est une fonction elle aussi (merci à tout le monde de ne pas introduire de maths post-bac dans ce fil...).

@+

[gondebaud]

la dérivée c'est donc (Xb - Xa )/( Yb - Ya) quand les point B et A sont très proches et on écrit parfois ( souvent ) dX /dY

Euh, c'est plutôt l'inverse : (Yb - Ya)/(Xb - Xa) et dY/dX.

Pour Fisikafon : le "quand les points B et A sont très proches" est une façon simplifiée pour décrire : 'B se rapproche de A le plus possible sans jamais l'atteindre" (la notion de limite pour ce sujet du post).

[Fisikafon]

Merci à tous, vos commentaires m'aident grandement !
Je pense que la notion de dérivée (concernant ce dont j'ai besoin évidemment) est à peu près rentrée. L'application à l'exercice pas totalement..
L'exercice qu'on a vu dans la cours est très semblable à ce que propose doul11, c'est un maitre nageur sur la plage qui doit sauver quelqu'un qui se noie, quel est le chemin le plus court pour aller la sauver ?
On a également procédé par la recherche de la pente nulle. Et c'est ça que j'ai du mal à comprendre, qu'est ce que cela est il censé représenter ?
Puis on en arrive après quelques étapes, à la conclusion que sini1/v1 = sini2/v2.

[coussin]

Une fonction c'est une certaine quantité (appelons la y) en fonction d'une autre (qu'on va appeler x).
À partir de là une question toute naturelle, je trouve, est de savoir comment varie y en fonction de x. C'est à dire, quand j'augmente x, est-ce que y augmente ou diminue ? C'est ça la dérivée.
La pente nulle, comme vous l'appelez, c'est une valeur particulière de x pour laquelle y ne varie pas. C'est bien évidemment une valeur remarquable (c'est la question naturelle qu'on se pose quand on a compris la dérivée).

[Duke Alchemist]

Re-

L'exercice qu'on a vu dans la cours est très semblable à ce que propose doul11, c'est un maitre nageur sur la plage qui doit sauver quelqu'un qui se noie, quel est le chemin le plus court pour aller la sauver ?
On a également procédé par la recherche de la pente nulle. Et c'est ça que j'ai du mal à comprendre, qu'est ce que cela est il censé représenter ?
Puis on en arrive après quelques étapes, à la conclusion que sini1/v1 = sini2/v2.

J'opte pour le chemin le plus rapide (ou le plus court en durée) plutôt que "court"...
Comme tu cherches la valeur minimale (la plus "courte"), c'est celle qui correspond à un sommet donc à une pente nulle soit à une dérivée nulle.

Duke.

[Fisikafon]

Je vois déjà un peu plus... Et oui effectivement je me suis trompée, je voulais parler de chemin le plus rapide.
Mais alors, ce qu'on cherche en calculant la pente nulle, ce n'est pas une distance mais une vitesse ? Et si je suis le commentaire de coussin, une vitesse qui ne varierait pas ?

[invite2313209787891133]

Bonjour

En réalité tu calcules des dérivées chaque jour sans même t'en rendre compte:
Lorsque tu te démarres avec ton scooter tu vas partir de 0km/h pour monter à 50km/h. Sur cet intervalle de temps ton accélération sera constante, ta vitesse augmentera linéairement, et la distance parcourue aura la forme d'une fonction du type y=ax² :


La pente, ou la dérivée de la distance en un point indique la vitesse à ce point. La dérivée de la vitesse en un point indique l'accélération.

[gondebaud]

@Fisikafon : L'instant où la vitesse serait nulle ou encore l'instant où la distance ne varierait pratiquement pas.

[Fisikafon]

D'accord, mais en quoi le fait que la vitesse soit nulle nous indique du chemin le plus rapide ?
Désolée si j'ai un peu de mal à comprendre ^^'

[coussin]

Quelle est votre courbe ? Quoi en fonction de quoi ?

[Duke Alchemist]

Re-

Peux-tu nous dire quelle est la courbe représentative que tu as à disposition ou que tu as tracée ?
Qu'est-ce qui est en abscisse et en ordonnée ?
Je pense que la confusion réside là.

N'oublie pas que pour une courbe donnée, tu obtiens la vitesse par la pente de la dérivée si la courbe tracée est la distance parcourue en fonction du temps !

Duke.

EDIT : Grillé... et pas qu'un peu...

[Fisikafon]

Justement ce n'est pas très clair dans mon cours...voici un schéma fait rapidement pour illustrer ma pensée, je pense que x représente le temps et y la distance. On recherche la durée la moins longue pour atteindre le point B.
Et c'est sur ce schéma que je ne comprends pas où se trouverait la pente nulle..
Et oui c'est assez confus dans ma tête. x)

[interferences]

Re,

Je trouve un peu difficile de demander de résoudre un problème à l'aide d'un principe variationnel, sans avoir vu la dérivée et l'intégration.
Peux-tu nous mettre l'énoncé ?

Au revoir

EDIT : Grillé, j'attends la validation de la pièce jointe.

[Fisikafon]

Il me semble qu'on cherche la dérivée de la courbe telle que la pente soit nulle...et c'est ça qui bloque. :S*
En fait le cour du prof n'est pas vraiment clair..

[coussin]

Il n'y a pas de pente nulle dans votre graphique. Impossible d'en dire plus sans savoir ce qui est en abscisses et en ordonnées.

[Fisikafon]

Je me disais aussi...qu'il y avait un truc qui clochait !
Je pense que je me suis trompée de graphique...je vais voir ça.

[Duke Alchemist]

Re-

Il serait mieux que tu nous envoie le schéma de la situation avec les données afin que l'on t'explique mieux.
Je sais à quoi il ressemble mais je voudrais voir les notations utilisées afin d'éviter des confusions.

Je pense que le graphique que tu devrais avoir est la durée du trajet en fonction d'une distance qui devrait être une fonction affine... mais tout dépend du paramètre choisi d'où ma demande ci-dessus

Duke.

[Fisikafon]

Le problème est qu'on a pas utilisé d'exemple précis, c'est une sorte de démonstration de la formule sini1/v1 =sini2/v2, et donc le principe de Fermat. :/ Et c'est aussi pour ça que je suis perdue. Je ne sais pas trop ce qui est représenté, la distance de la lumière par rapport au temps, et par conséquent j'ai du mal à voir le rapport avec la pente = 0...

[coussin]

Pour démontrer le principe de Fermat à votre niveau on prend un point dans le premier milieu, un point dans le deuxième milieu et on calcule la longueur optique en de la position d'un troisième point sur l'interface entre les deux milieux. On trouve que la longueur optique a un minimum (la voilà votre pente nulle...) à une certaine position de ce troisième point. Cette position très particulière de ce troisième point définie les angles d'incidence et refracté qui vous donne le principe de Fermat.

http://en.wikipedia.org/wiki/File:Snells_law.svg

On fait varier la position de O pour aller de P à Q.

[invite2313209787891133]

Bonjour

Il existe une façon plus intuitive de représenter ce principe, il suffit de diviser la longueur du trajet optique par l'indice de réfraction.
Si par exemple un rayon lumineux passe de l'air (n=1) à travers une plaque de verre (n=1.5) de 1cm d'épaisseur on peux imaginer que le rayon lumineux se propage en ligne droite lorsque le verre est "compressé" pour lui donner une épaisseur de 1/1.5cm.