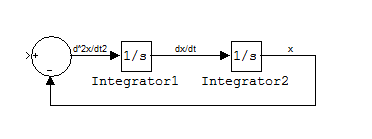
Je sais ce qu'est une intégrale mais je ne comprends pas bien ce que veux dire "un nombre d'integrations" ou du reste je n'utilise jamais cette terminologie. La raison en est que lorsque je modélise un système physique que je cherche à comprendre, je ne peux pas m'amuser à ajouter le nombre d'intégrations ou de dérivations que je veux, ils sont imposés par la physique des équations de Newton ou d'Hamilton.
Dans votre cas c'est different car vous pouvez introduire des éléments dans la dynamique qui jouent le role d'intégrateurs, dérivateurs etc...et finir avec des équations de la dynamique d'ordre 32 ou que sais-je. Ce genre de choses vous parait tout à fait normal à vous mais tout à fait bizarre à moi où pour moi l'ordre le plus élevé d'une équation de la dynamique que j'ai vu est celui de la force d'Abraham-Lorentz d'une charge accélérée sur elle même qui est d'ordre 3 et qui reste encore parfois débattue.
Non et je n'ai jamais dit que je le faisais...te remets tu à confondre calculs et physique ?Résolution classique par équatibn caractéristique.
Quand t'as une racine double, t'en vire pas une des deux parce que c'est la même et quelle n'apporte donc aucune information physique supplémentaire?
Si?
faut me donner le contexte mais les opérateurs sont clairement differents oui.d/dt + 1 et d^2/dt^2 + d/dt + 1 ce n'est pas pareil, on est bien d'accord?
certainement oui, c'est pour ça que l'équation de Schrodinger n'est pas du deuxième ordreSi oui, il y a la même nuance entre d^2/dt2 + 1 et d/dt + i..
Mais je crois qu'on en a fini quant au thème de ce fil non ? autre chose à ajouter ?
-----






 dont l'original est
dont l'original est