Vitesse de refroidissement d'un corps

[bibidou]

Bonjour,

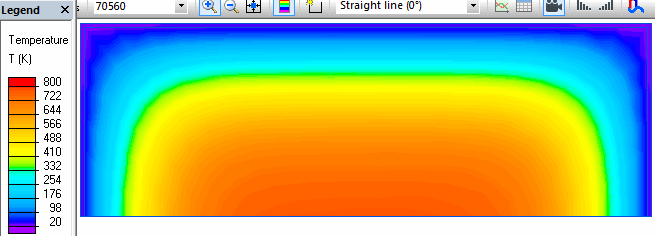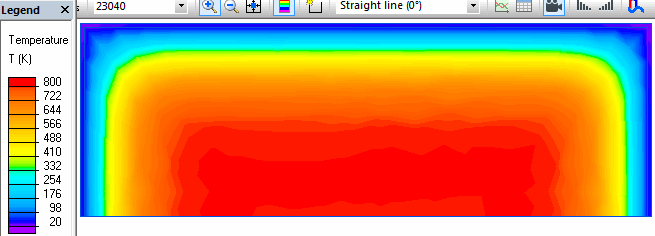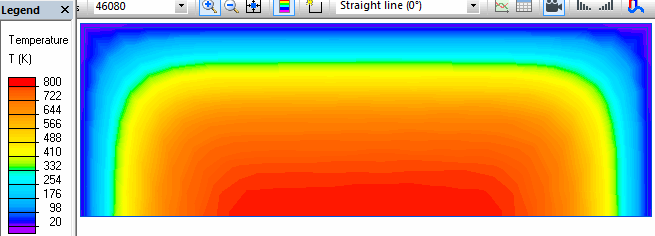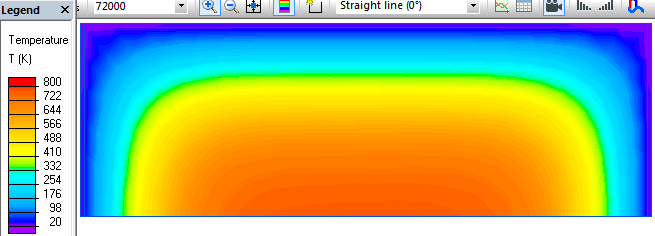
Je travaille sur un projet solaire et je cherche à déterminer temps de refroidissement d’un corps dont je possède très peu de donnée (cofalit).
J’ai vu qu’il existait les équations de Newton pour modéliser un refroidissement, cependant je ne trouve pas le coefficient de proportionnalité.

Est-il possible d’appliquer le raisonnement suivant, j’ai un gros doute sur l’utilisation de la conduction de cette manière :
- J’assimile mon corps à une sphère de rayon r et de masse m connues
- Je connais le Cp et le Lambda
- Je connais mon DT
- Je néglige dans un premier temps la convection avec l’air
Energie contenu dans ma sphère : E = m.Cp.DT
Flux thermique issu de ma sphère : P = - Lambda.S.DT/r
Donc temps = E/P

Je me suis dit que la conductivité de mon corps était sa capacité à céder son énergie.
Merci beaucoup pour votre aide.
-----

[Boumako]

Bonjour

La conduction va déterminer la répartition des températures à l'intérieur du corps, mais pour qu'il se refroidisse il faut qu'il effectue un échange avec le milieu, par convection, conduction et rayonnement. Tu ne peux pas les négliger, sinon le corps ne se refroidirait pas.

[bibidou]

Bonjour et merci pour ta réponse,

Je suis tout à fait d’accord avec toi, j’ai en fait du mal en fait à exprimer ce que je recherche.
Mon problème c’est qu’il s’agit d’un phénomène transitoire (le refroidissement) et que je suis un peu désemparé car mes connaissances en thermique se limitent à des phénomènes en régime permanent.

J’ai donc pensé qu’un corps avait une capacité maximale intrinsèque à restituer l’énergie emmagasinée en lui, et que le milieu allait pouvoir favoriser ce transfert jusqu’à cette limite (en fonction des coef de conduction et convection du milieu). Par exemple : même si on met une brique réfractaire à 500°C dans un milieu extrêmement propice à absorber son énergie, la brique ne deviendrait pas froide instantanément.

J’aimerai retrouver cette valeur limite si tant est qu’elle existe (mon raisonnement est-il juste?)!

[Boumako]

On peut dire que la brique "contient" une certaine quantité de chaleur qu'elle peux potentiellement restituer. Cette quantité est égale à Cp* masse *Dt (entre la température du corps et la température ambiante).
Cette énergie sera cédée vers le milieu par différents modes de propagation, proportionnellement à la différence de température entre le corps et le milieu. Ce coefficient de proportionnalité correspondant au coefficient d'échange global : Puissance cédée = Surface d'échange * coefficient global * Dt
La température du corps se calcule par l'équation suivante : t° corps = t° ambiante + (t° initiale - t° ambiante) *e(-t/)
avec = (masse * Cp) / (surface d'échange * coefficient globale d'échange).

Attention : Ceci ne fonctionne qu'avec un corps présentant une conductivité importante, qui permet de négliger les effets de conduction interne.

[A voir en vidéo sur Futura]

[bibidou]

Bonjour Boumako,
Merci pour ton aide, il faut encore que je potasse tout ça, mais tu m'as donné des pistes pour déterminer le coefficient de proportionnalité de l'équation de Newton.
Par contre j'avais lu ça http://www.madsci.org/posts/archives...0375.Ph.r.html
L'équation de Newton ne serait applicable que pour un refroidissement par convection, et pour le coup mon matériaux est plutôt réfractaire! :/

Pour complexifier le tout, j'ai en réalité mon matériaux + l'enceinte du contenant + mon fluide caloporteur pour accélérer le refroidissement. Je n'ai donc pas de convection pure.
Je peux faire varier le débit de mon fluide et la surface d'échange pour augmenter la puissance du flux. Mais ne suis-je pas limité par les propriétés même de mon matériaux à restituer son énergie?

[Boumako]

Oui en effet. Pour en être certain l'idéal serait que tu fasses un petit schéma (avec dimensions et épaisseurs) en donnant les valeurs de conductivité thermique de chaque matériau, je te dirais si il est possible d'utiliser des hypothèses simplificatrices.

[bibidou]

Merci encore pour ton aide.
J'essaie de faire un schéma potable dans la soirée!

[bibidou]

Bonsoir,
Voici enfin mon schéma. Dans cette phase du procédé le réfractaire devient un une réserve d'énergie que l'on souhaite soutirer.

En gros je peux paramétrer ma décharge en jouant sur le débit du fluide caloporteur (pour l'instant de l'eau pressurisée). Je connais l'énergie disponible via E=m.Cp.DT, et si je fixe un temps de décharge, j'ai ma puissance moyenne à évacuer (qui j'imagine va varier avec le refroidissement du réfractaire). C'est comme ça que j'ai procédé pour l'instant.

Par contre, pour faire l'analogie avec l'électricité, je me suis dit que quels que soient le "consommateur" mon stockage devait avoir une puissance de décharge maximum. J'aurais aimé la connaitre pour m'assurer que j'aurais la puissance voulue après échange avec le fluide calo.
D’où ma question initiale sur la conductivité.

J'ai l'impression d'être confus, j'espère que tu auras suivi le fil de ma pensée.

Merci pour ton aide

[Boumako]

Merci pour ces précisions.

Le problème est plus complexe que je le pensais, car la grande taille de l'objet, associé à une conductivité assez faible font que le champ des températures ne sera pas homogène. On va donc avoir une puissance dégagée qui sera fonction de la différence de température entre l'interface et l'eau, et une température à l'interface fonction de la vitesse à laquelle se refroidit le corps. Par ailleurs l'objet va se refroidir plus rapidement dans les angles.
Il y a aussi un autre paramètre a prendre en compte : Refroidir un tel objet avec de l'eau n'est pas réaliste, des contraintes importantes vont se former dans la structure en acier, qui peuvent aller jusqu'à la rompre. En outre l'eau ne peux pas échanger avec une telle différence de température (on peut difficilement dépasser 50/80°C au dessus de la température d'ébullition).

Si ce problème est d'ordre pratique ce n'est pas du tout réaliste. Par contre si la démarche se veux purement intellectuelle tu peux jeter un œil à cette simulation que j'ai faite, qui te donnera une idée du comportement des températures. J'ai supposé l'objet immergé dans une eau à 20°C. Le temps qui défile est exprimé en secondes, donc la simulation coure sur 20 heures.
L'objet est vu en coupe, son axe est en bas et je l'ai supposé en forme de cylindre, de 1m de rayon sur 3m de haut. Il faut que tu imagines qu'il a été coupé en 4 parts égales en suivant l'axe et que tu observes la coupe d'une des parts.

[bibidou]

Boumako, je ne peux que te remercier, je ne pensais pas que tu irais jusqu’à faire une simulation !
(D’ailleurs quel logicielle utilises-tu ? Ca à l’air d’être pas mal)

Effectivement il s’agit plutôt d’une vue de l’esprit afin de comprendre le phénomène de décharge thermique, mes régimes de températures ne sont pas encore définies. Par contre j’avais conscience des contraintes sur les matériaux, c’est pour ça que j’avais fixé une épaisseur conséquente d’acier et que l’eau est pressurisée pour travailler avec un point d’ébullition plus élevé (l’eau n’est pas introduite froide mais préchauffée). Mais bon, rien n’est fixé, je prends bonne note de tes remarques.

Hormis l’aspect résistance des matériaux, pourquoi est-ce que l’eau ne peut pas échanger avec une grosse différence de température au-dessus de son point d’ébullition ?

Toi qui a de bonnes connaissances en thermique, peux-tu me répondre stp sur l’analogie avec l’électricité dans mon poste précédant? Un matériau à t-il une capacité de décharge maximale indépendante du milieu qui va absorber l’énergie ?

En te remerciant pour le temps que tu me consacres

[Boumako]

Pour le logiciel j'ai utilisé Quickfield.
Même si l'eau est préchauffée la différence sera encore trop grande ; la température maximale que l'eau liquide peux atteindre est de 374°C (température critique). Il faut une différence de température plus faible pour éviter que de la vapeur se forme à l'interface, ce qui isole l'eau liquide de la paroi chaude. Ce phénomène disparait brutalement en dessous d'une certaine température. Tu trouvera plus d'infos ici : http://fr.wikipedia.org/wiki/Cal%C3%A9faction

Une meilleure solution serait de refroidir par un mélange d'air pulsé et d'un brouillard d'eau. L’énergie peut être récupérée par condensation de cette eau avec un échangeur vapeur/liquide.

En ce qui concerne le dernier point je ne vois pas ce que tu veux dire par décharge maximale.

[bibidou]

Ok, merci pour ces précisions, je vais regarder ça !

Pour ma comparaison avec l’électricité un exemple pour illustrer mes réflexions :
Une batterie (stockage d’énergie) est limitée de par ses propriétés dans la puissance maximale qu’elle peut délivrer, et ce quels que soient les « consommateurs » de cette puissance. Elle ne se décharge pas instantanément (cinétique chimique ?). J’imagine qu’il en est de même pour un condensateur même si la décharge est beaucoup plus rapide.

Je pensais que mon stockage d’énergie thermique avait une puissance de décharge maximale du fait de sa géométrie et surtout de ses propriétés thermiques (ex : s’il est dense et volumineux sans grande surface d’échange, l’énergie aura à traverser le matériau qui présente une résistivité), même si par une vue de l’esprit on avait un échange optimal avec le milieu.

En gros si je disais que mon matériau se présentait sous forme de sphère d’un rayon important, et donc que l’on ne peut pas négliger sa conductivité, qu’elle serait la puissance max qu’il pourrait délivrer à un instant t si je fixe la température à l’interface en considérant que l’échange est parfait.

C'est tordue comme réflexion mais c'est juste pour me permettre de bien comprendre les phénomènes.

Je ne suis pas sur d'avoir internet durant le WE, ne t'étonne pas si tu as une réponse seulement mardi, je suis tes postes avec attention.

[Boumako]

La puissance max correspond au delta de température (paroi - milieu) multiplié le coefficient d'échange, mais celle ci va chuter très rapidement car la température à l'interface va chuter.

Voici ce que l'on obtiendrait avec l'exemple donné plus haut avec l'objet immergé dans une eau à 20°C, en admettant que l'échange ne soit pas perturbé par des phénomènes de caléfaction :


Si on stoppe l'échange la température à l'interface va remonter, et la puissance libérée va augmenter dès que l'échange se produira à nouveau (sans toutefois jamais dépasser ce que tu avais au départ).

Je te propose une petite expérience pour illustrer ceci : Tu plonges un œuf dur qui sort de sa casserole d'eau bouillante dans de l'eau froide. Très rapidement tu va pouvoir toucher l’œuf sans te bruler, mais si tu le sors de l'eau tu le sentira redevenir chaud, ou redevenir froid si tu le plonge de nouveau dans l'eau, et ceci en quelques secondes.

[bibidou]

Merci Boumako,

Je pense avoir compris le phénomène, la puissance maximale dépend bien entendu de la différence de température avec l’interface.

Par contre ça soulève une question complémentaire, qui je crois est la base de mes difficultés : Comment se caractérise le coefficient d’échange dans un cas où on met en contact 2solides (donc avec pour seul effet la conduction) ? Qu’est-ce qu’il faut prendre en compte du coté de mon corps et du côté de l’interface ? De ce que j’avais compris, la conduction dans un corps dépend de ses dimensions, est-ce qu’il faut donc considérer son rayon sachant que passé t0 la température ne sera pas uniforme en son sein ?

Un exemple pour illustrer :
J’ai une boule de cuivre de rayon 1m, avec une température de 400°C, supposé uniforme. Je l’enterre dans du sable suffisamment fin pour considérer qu’il n’y a pas d’air et que le transfert se fait sur toute la surface de la sphère. La boule est au milieu d’un volume de sable suffisamment grand pour être considéré comme infini.
Comment caractériser le coefficient de transfert dans un cas comme ça (prise en compte des dimensions de la sphère, épaisseur de sable non définie) ?

J’espère que toutes ces questions ne sont pas trop « prise de tête »…

[Boumako]

Si je reprend ton exemple la boule va céder sa chaleur au sable, celui ci va chauffer sur une petite couche qui entoure la boule, puis cette couche va à nouveau chauffer une petite couche immédiatement autour etc.
Le flux en un point donné est égal à - dt/de * S * avec t pour la température et e pour l'épaisseur (je néglige l'influence sphérique de la transmission pour ne pas alourdir l'équation).

Ce flux de chaleur est responsable de l’élévation de température du milieu qu'il traverse, et cette élévation de température va provoquer un flux de chaleur un peu plus loin, et ainsi de suite : La chaleur se propage par conduction.
Je ne sais pas si ça répond à ta question...

[Boumako]

Ce sera peut être plus parlant avec cette appli en ligne : http://www.lmm.jussieu.fr/~lagree/SO...ite/index.html

[bibidou]

Bonjour Boumako,

Merci de continuer de te pencher sur mes questions.

Oui du coup le phénomène de diffusion dans le sable je l’avais compris et avec l’accroissement du rayon, la puissance par unité de surface diminue lorsque l’on s’éloigne de la sphère.

Ma question est plutôt sur comment calculer la puissance émise par la sphère à l’interface avec le sable (admettons à 20°C à t0, avec un lambda de 2 W/(m.K)) ? Faut-il prendre en compte seulement la conductivité du sable, ou celle du cuivre (sur qu’elle épaisseur ?), ou les deux conductivités ? Et qu’elle forme prend l’équation ?

Disons juste déjà pour raisonner à t0 car après si je ne me trompe pas ça se corse, parce que d'un coté la température de peau de la sphère va diminuer, mais de l'autre la température du sable va augmenter...

[bibidou]

Je vais étudier la partie "résolution implicite" du lien que tu m'as envoyé, en espérant que soit à ma porté!

[Boumako]

En fait on ne peux pas vraiment répondre à cette question, car le phénomène est transitoire, mais sur une petite épaisseur e on peut dire que le flux qui traverse e est égal à la différence de température (entre les 2 cotés de e) divisé par / e

[bibidou]

Bonjour,

Oui je sais que toute la difficulté vient du fait que l’on soit en régime transitoire, c’est beaucoup plus abordable pour moi en régime établi.

Par contre, c’est bien divisé par « Lambda/e » ? Car dans l’équation qui exprime la puissance en régime permanent lamda/e est facteur du delta T, non ?

Autre chose, on parle de lambda/e. J’en conclu donc que l’on réfléchit au sein d’un des corps, le cuivre ou le sable. Mais que ce passe-t-il à l’interface ? Car si j’ai bien compris tes postes précédents, la puissance émise par la sphère chaude à t0 dépend de la différence de température entre le cuivre et le sable (toutes deux considérées comme uniformes). Il s’agit donc d’un delta T à l’interface. Le flux est-il fonction du lambda du cuivre ou de celui du sable ?

Je pose beaucoup de questions, j’espère ne pas t’ennuyer.
En tout cas j’ai déjà une meilleure compréhension du phénomène depuis le début de la conversation.
Merci pour ton aide.

ps : comment fait-on pour écrire des lettres grecques et des formules sur le forum? J'ai cherché un peu mais je n'ai pas trouvé.

[enpiste]

svp moi aussi j'ai un exercice à propos de ça et je n'arrive du tt à le résoudre
voice l'énonce de l'exo :

La vitesse de refroidissement d’un corp est proportionnelle ́a la différence de tempéarature entre ce
corps et celle du milieu ambian. On suppose que la température de l’air ambiant est constante et
égale ́a 20◦C. Dans ces condition on observe que la température du corps passe de 100◦C ́a 60◦C
en 15 minute. Au bout de combien de temps se trouvera t-elle ́a 30◦?

qlq'un pour m'aider?

[gts2]

Vous avez regardé la date ?
Il serait peut-être plus efficace de créer un nouveau sujet.