Moments d'inertie d'une demi-boule

[invite8653e861]

XXXXXXXXXXXXXX


Bonjour, après un petit calcul, j'ai trouvé:

Ioz=? (2/5)MR²
Iox=Ioy=? MR²/5

pour les moments d'inertie d'une demi-boule de rayon R et de masse M.

j'ai un doute sur mes résultats pourriez vous me dire quelles sont les valeurs des moments d'inertie pour ce volume s'il vous plaît.

Ensuite je me demandait si l'on pouvait utiliser le moment d'inertie par rapport à un point (centre de la demi-boule) pour calculer les moments d'inertie par rapport aux axes?
A priori je pense que non, puisque on utilise le fait que dans une boule ou une sphère les moments d'inertie par rapports aux 3 axes sont égaux pour introsuire le moment d'inertie par rapport à un point, or sur une demi-boule, il me semble que Ioz est différent de Iox et Ioy.

mais j'aimerais aussi avoir votre avis là-dessus


merci par avance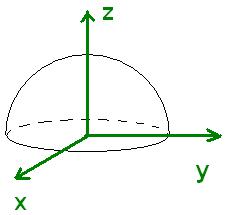
-----

[mécano41]

Bonjour,

Il doit y avoir un problème car l'inertie d'une sphère pleine autour de Oz est déjà : J=2.M.R²/5

L'inertie de la demi-sphère autour du même axe est donc la moitié soit : J=M.R²/5

Autour de l'axe Ox ou Oy, ce doit être la même chose. Je n'ai pas vérifié mais dans l'intégrale triple, on intègre de 0 à Pi au lieu de 0 à 2.Pi mais comme le 2.Pi ou le Pi peuvent se mettre en facteur, il sortent de l'intégrale. Le facteur 2 influe donc directement sur le résultat.
C'est d'ailleurs assez logique : imaginons deux demi-sphères collées sur l'axe Ox par exemple. Leur inerties sont égales et elles s'ajoutent puisqu'on est autour du même axe. Elles forment une sphère dont l'inertie est J=2.M.R²/5. La moitié est donc J=M.R²/5.
Ce qui a peut-être tendance à gêner notre raisonnement logique c'est qu'autour de l'axe Oz, on est équilibré alors qu'autour de Ox ou Oy on est complètement déséquilibré.

Cordialement

[invite8915d466]

Bonjour,

Il doit y avoir un problème car l'inertie d'une sphère pleine autour de Oz est déjà : J=2.M.R²/5

L'inertie de la demi-sphère autour du même axe est donc la moitié soit : J=M.R²/5

mais la masse est aussi divisée par deux, donc la formule reste la même avec 2/5.

[mécano41]

Bonjour GillesH38,

C'est vrai ! J'ai honte ! Il y a des soirs où l'âge se fait durement sentir

Merci

Amicalement

Mes excuses à Faroux51!

[A voir en vidéo sur Futura]

[invite8653e861]

il n'y a pas de mal, merci pour vos réponses, il ne me reste plus qu'a trouver ou est mon erreur pour Iox et Ioy

[invite76303089]

mais la masse est aussi divisée par deux, donc la formule reste la même avec 2/5.

Mais attend, si la masse est aussi divisée par deux , alors le résultat n'est pas encore divisé par deux au lieu d'être multiplié par deux comme tu viens de le faire ?

[invite6dffde4c]

Bonjour.
Le moment d'inertie est la moitié de celui d'une boule entière (1/5)MR² avec M de la boule entière.
Et (2/5) MR² avec le M d'une demi-boule.
Et c'est la même chose (2/5) MR² pour les axes x et y, pour les mêmes raisons.
Au revoir.

[invite824965ae]

Bonjour,

En fait tu as la même formule MAIS PAS AUTOUR DE L'AXE DE GRAVITE.

Pour avoir autour de l'axe de gravité (G), il faut appliquer Huygens. I(O) = I(G) + f(OG). Tu auras donc une inertie plus petite au centre de gravité.

*** Je n'ai pas encore regardé ta formule. Je te relis et je complète.

*** Bon, j'ai vu le lien, c'est juste le dessin de la demi-boule (ce serait le même dessin pour une demi-sphère)

Donc, en mécanique classique (dynamique) on a : J = ∫∫∫(dm r²) = µ ∫∫∫(dv r²), où r est la distance à l'axe de rotation.

(En mécanique des matériaux, on a I(Oy)(section) =∫∫(section) z²dydz d'où Huygens I(Oy) = I(Gy) + OG²S mais ce n'est pas je crois le moment quadratique statique que tu cherches)

Donc pour retrouver Huygens en dynamique classique, on calcule J en G et J en O :

J(Ox) = µ ∫∫∫(dv r²) = µ ∫∫∫(dx dy dz)[(y-y0)²+(z-z0)²] = µ ∫∫∫(dx dy dz)[(y-yG)²+(yG-y0)² +2yGy0 + (z-zG)² +(zG-z0)²+2zGz0]
=J(Gx) + µ ∫∫∫(dx dy dz)[(yG-y0)² +2yGy0 + (zG-z0)²+2zGz0]

Si j'ai bonne mémoire Huygens dit (donc le prof dit) que G étant le centre de gravité, l'intégrale de deux des termes s'annule (je ne me souviens plus la démonstration mathématique, ça marcherait mieux en vectoriel, je ne sais le faire que sur papier ) :
Mais je constate que la formule de Huygens http://fr.wikipedia.org/wiki/Th%C3%A..._de_Steiner.29 est la même en modèle quadratique et en modèle dynamique.

J(Oy) = J(Gy) + Md² où d est la distance entre les axes

(Par exemple pour un point matériel, I(G)=0 ; s'il est au bout d'une ficelle et tournoie à la distance d, Huygens donne I(O) = Md² qui est bien égal à la formule connue I = MR² pour un point ou un anneau tournoyant à la distance R de l'axe)

JOz(hémisphère) = Joz(sphère) par symétrie (en effet Oz=Gz donc d=0 sous cet axe, on a bien (2/5)(MR²) comme tu avais trouvé)

Maintenant, quelle est la hauteur zG du point G, afin de déterminer J(Gy)=J(Gx) (symétrie) =J(Ox) - Md² (tu as déjà calculé J(Ox) =MR²/5) ?

Hier soir j'ai trouvé sur une feuille zG/R = U répondant à l'équation U(1-U²/3)=1/3, avec U~0,31, voici pourquoi je venais chercher sur le net la valeur exacte, que tu apparais en première page des recherches Google car il n'y a pas de point d'interrogation et que tout le monde clique sur ton lien en croyant y trouver la réponse.
Il faut donc que quelqu'un y place la réponse - bien ou mal formulée - afin que tous les cliquants successeurs y trouvent effectivement la réponse.

Ma réponse pour l'instant :
J(Ox) = J(Gx) + Md² où d est la distance entre les axes Ox et Gx
J(Oy) = J(Gy) + Md² où d est la distance entre les axes Oy et Gy
J(Oz) = J(Gz) = (2/5)MR²
Tu as déjà calculé J(Gx)=J(Gy)=MR²/5
d est aussi la hauteur zG, valeur théorique non vérifiée UR, avec U(1-U²/3)=1/3, valeur numérique non vérifiée 0,31R

[invite824965ae]

Complément important : d = zG = 3R/8 voir http://forums.futura-sciences.com/ph...ml#post4527564 message de ce jour.
(valeur confirmée par deux sites)

[invite8273ef95]

guys, je veux savoir la matrice d'inertie pour une demi-sphere pleine