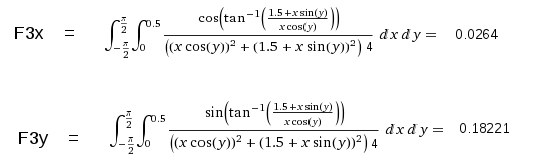Calcul d'une résultante de force due à une pression

[yy527]

Bonjour

Je dois calculer la la résultante d'une force et je trouve une différence entre le calcul par intégral et le calcul fait avec un programme. Je ne sais pas si mon intégrale est bien posée. La force en question provient des forces de pression sur un demi cercle. Je prends un exemple simple, un demi disque est rempli d'un fluide et l'attraction (comme la Terre mais considéré en un point) attire le fluide et met en pression la paroi. Je cherche à calculer la force au centre de ce cercle. La loi est simple c'est 1/d² avec d la distance.

Voici un dessin:

sx1.png

Attention, pour l'intégrale qui suit, le zéro de l'intégration est en haut (la verticale) et je j'intègre en horaire pas en trigo.
Ensuite, pour l'intégrale j'ai ceci:

sx2.png

La force F2x est la force horizontale au centre du demi disque et F2y esst la force verticale au centre. La pression en un point est avec . Ensuite je multiplie par le sin(x) pour la force verticale et par cos(x) pour la force horizontale.

Je ne donne pas mon programme car une fois que je serai certain d'avoir bon à l'intégrale je trouverai plus facilement mon erreur.

Voilà si vous avez une idée de mon erreur ?

++
-----

[LPFR]

Bonjour.
Tout votre problème est mal posé.
La pression est une force divisée par une surface. Dans un univers à deux dimensions vous ne pouvez pas avoir de pression. À moins que ce soit l’équivalent de la pression en « Flatland » : force/longueur.
Et évidement, la dépendance avec la distance n’est plus 1/d² mais 1/d.

Vous avez deux options pour rendre votre problème possible en 3 dimensions : utiliser une demi sphère au lieu d’un demi-cercle ou utiliser un demi cylindre infini.
Au revoir.

[yy527]

L'objet a une profondeur mais très faible pour ne pas tenir compte des effets dus à la distance qui change. C'est pas possible de poser une profondeur très faible genre 1e-10 ou moins ? c'est juste pour voir le raisonnement ?

Merci

[phys4]

En supposant que votre demi cercle soit une couche mince, les intégrales sont bien posées.
Je n'ai pas vérifié le calcul.

La définition du point d'application des forces comme le centre du demi-cercle n'est pas correcte, la résultante n'est pas au centre.

[A voir en vidéo sur Futura]

[yy527]

La définition du point d'application des forces comme le centre du demi-cercle n'est pas correcte, la résultante n'est pas au centre.

@Phy4: La définition du point d'application pour le demi cercle ou pour le demi cercle + paroi à gauche ?

Merci

[phys4]

Le point d'application de la moyenne des forces est obligatoirement sur la paroi de gauche, pour cette paroi.

Pour le demi cercle, elle est quelque part dans le demi cercle, et ne pas être sur la paroi de gauche.

[yy527]

La force de pression n'est pas perpendiculaire à la surface ? et dans ce cas toutes les forces de pression passent par le centre du cercle. Je ne comprends pas pourquoi F2x et F2y ne sont pas mis sur le centre du cercle si vous pouvez m'expliquer ?

Merci

[phys4]

La force de pression est bien perpendiculaire à la surface en chaque point.
Comme la force varie sur le demi cercle, sa moyenne n'est pas simple, et la moyenne ne peut être au centre du cercle que pour un cercle complet.

[yy527]

Pour avoir la résultante de N forces passant par le même point, je ne peux pas faire la somme des N vecteurs et donc avoir comme point d'application le centre du demi disque (là où je met la point du compas pour tracer le cercle) ?

[phys4]

Le point d'application moyen correspond à la notion de centre de gravité. Il faut faut construire par intégration le point d'application moyen en pondérant par le force en chaque point.
Pour un demi-cercle, il est évident qu'il se trouve à l'intérieur du demi-cercle et ne peut se trouver sur le bord.

Ce type de problème est simple pour un attracteur à l'infini, mais devient complexe pour une forme quelconque avec un attracteur à distance finie.

Pour une force en 1/ d² et une forme sphérique, le centre d'attraction est au centre de la sphère (démonstration de Newton), pour tous les autres cas c'est différent.

[yy527]

Ah pardon, j'ai oublié de dire que le demi disque possède un axe de rotation qui est situé au centre du cercle, dans ce cas la résultante peut se tracer au centre ?

Merci

[phys4]

Le centre d'application moyen ne dépend que de la position de votre demi-cercle. Un axe ajoute la possibilité d'un couple de rotation autour de cet axe.

Si l'axe se trouve dans le plan déterminé par le point d'application et la force moyenne, alors le demi cercle aura un couple de rotation nul, et inversement.

[yy527]

On parle bien uniquement de la paroi formée par le demi cercle pas de la paroi rouge ? Si je fais la somme des forces avec le demi cercle et la paroi rouge alors je comprends que le point d'application ne soit pas le centre du cercle. Mais si je n'ai que la paroi formée par le demi cercle alors graphiquement (géométrie) si je fais la somme de N vecteurs qui passent par le centre du cercle alors le vecteur final a pour origine le centre du cercle, donc si ce n'est pas le cas comment je fais pour graphiquement le constater ?

Merci

[phys4]

La totalité des forces a pour centre de gravité le barycentre d'attraction situé un peu à droite de l'axe y.
Mais les forces appliquée sur la paroi centrale ont bien un centre d'application situé sur cette paroi, en non à l'infini, point de concours des supports des forces.

Cela implique que le centre d'application moyen pour le demi-cercle soit bien à l'intérieur du demi-cercle.

Pour trouver le centre d'application il faut prendre le point d'application de chaque élément de force, donc situé sur le demi cercle, et faire la somme pondérée en x et y.

[yy527]

Bonjour

Merci beaucoup pour vos explications.

J'ai également calculé la force que subit l'objet rouge (point ponctuel) qui attire, et j'ai trouvé cela:



Avec F3x la force en horizontal et F3y la force en vertical.

Est-ce que c'est correct ? Comme c'est une intégrale double, je ne suis pas certain d'avoir mis les bonnes bornes et j'ai dû diviser par 4.

Bonne journée

[phys4]

Vous avez fait beaucoup de calculs,

vous remarquez que la force en y est presque égale à celle de la paroi en demi-cercle. Elles devraient être rigoureusement égales, car il n'y a pas d'autre force dans ce sens, il doit exister une petite erreur dans l'un des deux calculs.

Pour Fx vous devez obtenir la différence entre les forces sur la paroi droite et la paroi courbe, la grandeur semble correcte.

[yy527]

Oui, les forces en 'y' sont rigoureusement les mêmes (avec un programme précis) mais ce que je ne suis pas certain c'est la méthode, est ce que les intégrales doubles sont bien posées: bornes, et la division par 4 ?

Merci

[phys4]

La division par 4 n'est pas naturelle.

Il y a un mystère dans vos intégrales : l'intégrale double sur une surface s'écrit en y quand il s'agit de longueurs, mais elle doit s'écrire en a en coordonnées polaires lorsqu'un angle figure dans les variables ?

Le facteur 1/4 pourrait être une correction liée à cette erreur.

[yy527]

J'ai pas bien compris, c'est r*dr*da ? R vaut 0.5. Qu'est ce que je dois changer dans l'intégrale pour l'écrire correctement ?

[phys4]

Les limites d'intégration et les variables de l'intégrale double s'écrivent comme ceci :

[yy527]

Pour les bornes ok, mais comment mettre la première intégrale dans la deuxième ?

En fait ce sont carrément mes coordonnées dans l'intégrale qui ne sont pas polaires ? car avec le "r.dr" cela donne divisé par 2 mais d'où vient l'autre division par 2 ?





Merci

[phys4]

Du fait que vous avez écrit sin(y) et cos(y) signifie que y est un angle entre les bornes d'intégration.
Normalement il faut laisser les éléments différentiels avec chaque signe d'intégration pour identifier à quelle coordonnée s'applique les bornes.

Ici il est évident que [-pi/2, +pi/2] doit s'appliquer à y, et donc l'autre à x; mais s'il y avait ambiguïté, l'écriture serait indéterminée.

[Dynamix]

Salut
x ne varie pas de -π/2 à +π/2
Tu nous fais un joyeux mélange de polaire et de cartésien .

[yy527]

Merci pour vos réponses. Oui Dynamix, je pense aussi que j'ai mélangé les deux, mais comment faire pour n'avoir que l'un ou l'autre ?
Les calculs sont bons du coup ?

[Dynamix]

Poser la question à gg0

[LPFR]

Les limites d'intégration et les variables de l'intégrale double s'écrivent comme ceci :

Bonjour.
J’ai constaté que cette expression était mieux comprise si on l’écrivait sous cette forme :



Au revoir.

[yy527]

Merci LPFR, oui, en effet je comprends mieux écrit comme cela, si j'intègre ce que vous me donnez cela donne , c'est cela ? enfin je sais pas vraiment si je dois l'intégrer ou s'il faut reprendre mon intégrale, je dois intégrer ce coef dans l'intégrale avec le et dans ce cas cela donne un coef de ?

[LPFR]

Re.
La façon d’écrire l’intégrale double avec les crochets, ne sert qu’à faire passer la façon « grande personne » de les écrire (celle utilisé par Phys4), qui peut être un peu déroutante pour les débutants.
En tout cas le résultat est bien 0,5xπ.
Mais tenez compte de l’observation de Dynamix à propos du mélange polaire cartésienne.

Je ne peux pas vous conseiller sur le fond. Je n’ai pas compris votre problème depuis le début. Et comme Phys4 l’avait compris, je ne me suis plus intéressé.
A+

[phys4]

J'avais repris votre ordre d'écriture, bien que ce ne soit pas la meilleure,
il vaut mieux effectuer d'abord l'intégration sur l'angle à distance au centre x constante, pour finir par intégrer sur la distance car celle-ci est une constante pour l'autre intégrale.

En faisant ainsi, les coefficients parasites devraient disparaitre.

[Dynamix]

La pression en un point est avec [IMG]http://www.futura-sciences.com/cgi-bin/mimetex.cgi?L=\sqrt((0.5*cos(x ))^2+(1.5+0. 5*sin(x))^2)[/IMG]. Ensuite je multiplie par le sin(x) pour la force verticale

En multipliant une pression par un nombre sans dimension , tu obtiens une force .
C' est curieux