Calculs des vecteurs forces

[invitef29758b5]

Si vous pouvez me dire quelle force est incorrecte ça m'aiderait

Quelle force est incorrecte d' après toi ?
Moi , je ne vois pas ...
-----

[invite8e757dd6]

J'ai pas fait d'erreur (pour une fois) ?

[invite8e757dd6]

Bonjour,

J'ai re dessiné les forces:



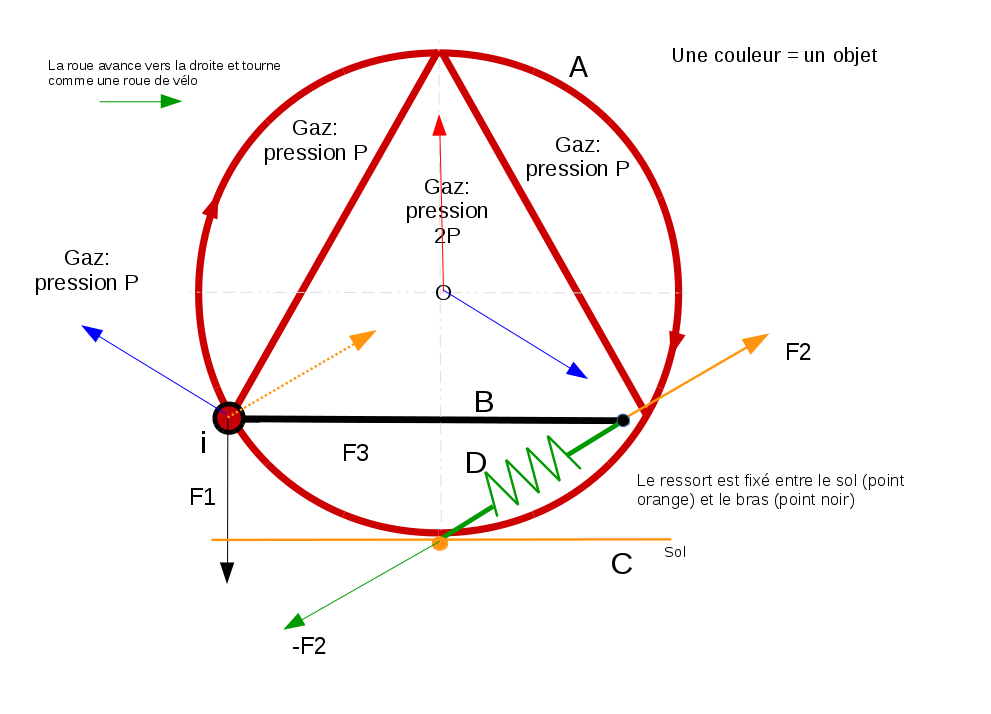
C'est cela ? avec chaque force à sqrt(3) ?

a+

[antek]

C'est un exercice sans doute intéressant à condition de connaitre toutes les données.
Pour ma part je ne vois pas le triangle équilatéral dont il est fait mention au début.

[invite8e757dd6]

Bonjour,

Les deux traits rouges et le trait noir réalisent un triangle équilatéral, non ? Même si ce sont 2 objets différents (une couleur = un objet). C'est quoi que vous ne comprenez pas ?

Je pense que mes forces dans mon premier dessins sont correctes, mais si je veux simplifier cela peut donner cela :



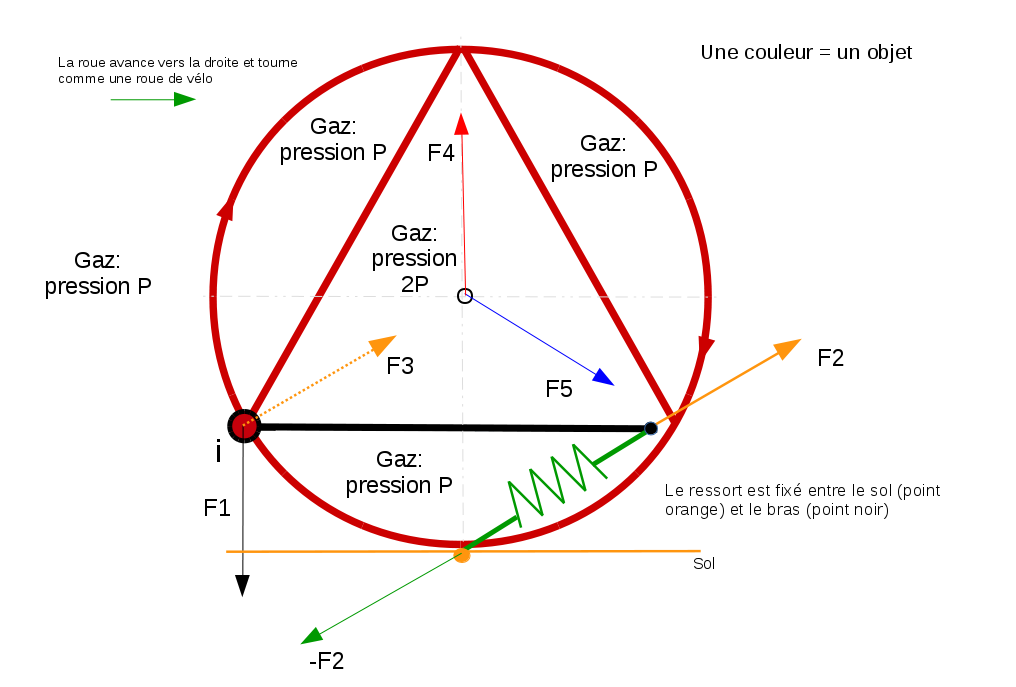
Ainsi, toutes les forces valent sqrt(3) N. Le moment que doit annuler le ressort est de 1.5 Nm.

F1 provient de la différence de pression sur le bras noir
F2 provient du ressort
F3 provient de F2
F5 provient de F3+F1 (en vecteurs)
F4 provient des forces sur les bras rouges

Merci

[invite51d17075]

a ta place, et depuis le début, je me serais contenté de décrire les forces et donc les moments qui concernent uniquement le bras noir.
si F1 est la force due à la diff de pression et exercée sur le bras noir, elle ne s'applique pas au point I.
F2 par contre s'applique bien à l'extrémité du bras.
si tu n'applique pas les forces au bon endroit, tu feras un calcul erroné pour les moments.

quel est le sens de "provenir de".?

[invitef29758b5]

F1 provient de la différence de pression sur le bras noir
F2 provient du ressort
F3 provient de F2
F5 provient de F3+F1 (en vecteurs)
F4 provient des forces sur les bras rouges

De la rigueur SVP !
Les forces sont des interactions , qui impliquent nécessairement deux objets .
Dans la description de tes forces on devrait trouver les noms de ces deux objets et le sens de l' action (A sur B ou B sur A)
Exemples :
F1 est la résultante des forces de pression sur B (moment nul au milieu du bras , c' est donc la qu' il faut placer la flèche)
F2 est la force appliquée par D à l' extrémité x de B .

F3 , je ne vois pas de quel objet il vient , ni sur quoi il s' applique .
Les deux autres encore moins .

[invite8e757dd6]

Alors avec des couleurs pour montrer les forces sur chaque objet:



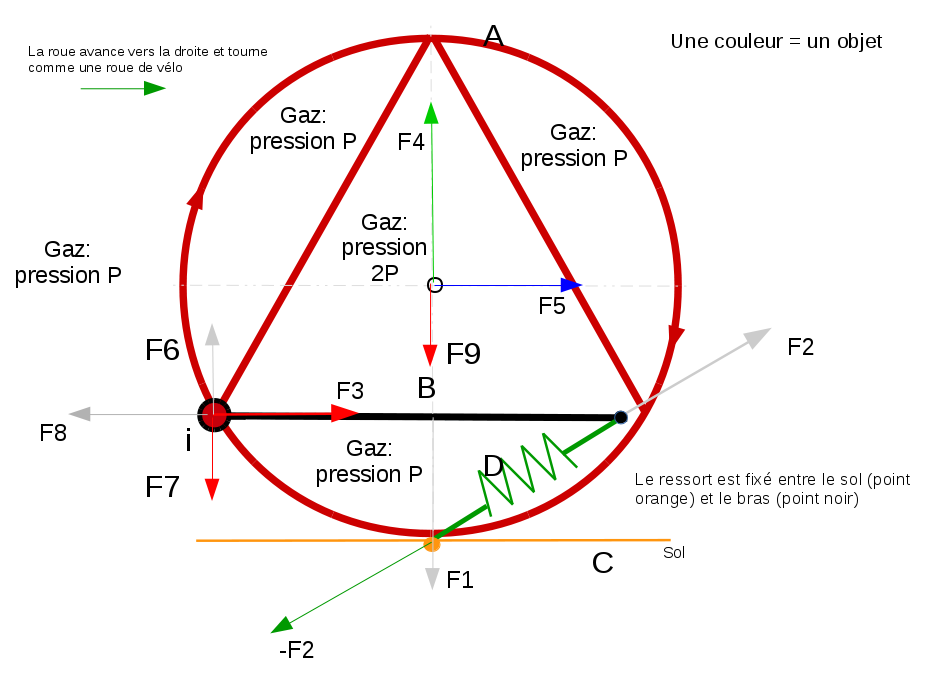
La barre noire (B) reçoit F2 du ressort, F1 de la pression, F6 de la réaction de l'axe, F8 de la réaction de l'axe (i).

L'axe rouge reçoit F3 et F7, ces forces proviennent de la barre noire (B)

Le centre de la roue (A) reçoit F4 provenant de la pression sur les murs rouges, F5 provenant du repport de la force F3 et F9 provenant de la force F7

@ansset: quand je dis provient, c'est parce qu'il y a un axe de rotation pour la barre et que la force sera transmise au centre de l'axe, l'axe réagit et fournit à la barre la force inverse (négative), l'axe a donc un couple au final. Après pour le centre de la roue, j'ai supposé que la masse était importante et concentré sur le centre mais je ne sais pas si cela entre en jeu, Dynamix dit que non.

Merci

[antek]

Les deux traits rouges et le trait noir réalisent un triangle équilatéral, non ?

Pour moi non !
Mais je suis la discussion avec intérêt.

[invitef29758b5]

La barre noire (B) reçoit F2 du ressort, F1 de la pression, F6 de la réaction de l'axe, F8 de la réaction de l'axe (i).

En fait il n' y a que trois forces sur B : F1 , F2 et Fi (action A sur B)
F6 et F8 , c' est une décomposition de Fi en x et y , pas forcément utile .

L'axe rouge reçoit F3 et F7, ces forces proviennent de la barre noire (B)

A reçoit de B la réciproque de Fi = -Fi (action de B sur A)

Le centre de la roue (A) reçoit F4 provenant de la pression sur les murs rouges, F5 provenant du repport de la force F3 et F9 provenant de la force F7

Le "report" d' une force , c' est du charabia .
F5 est l' action de qui sur qui ?

[invite8e757dd6]

J'ai décomposé car pour moi c'est plus simple de réfléchir d'où vient quelle force mais effectivement au final c'est une somme de vecteurs sur un point.

La pourtour de la roue a une masse ainsi que le centre. La pourtour de la roue est en rotation autour du centre, même si la roue avance (sans frottement sur le sol, je pense que c'est important), elle tourne aussi et pour moi comme l'axe (i) reçoit -Fi, il va "je sais pas comment on dit alors" cette force sur le centre de masse de la roue, le pourtour externe de la roue subit un moment à cause de -Fi mais comme le centre va réagir, le pourtour va finalement recevoir un couple.

[invitef29758b5]

le pourtour va finalement recevoir un couple.

Il faut au minimum deux forces pour produire un couple .
A reçoit l' action de B : résultante -Fi , moment Mi en i = 0
De la tu peux déterminer le moment Mo de cette action en o

[invite8e757dd6]

Avec les forces Fi et Fo:



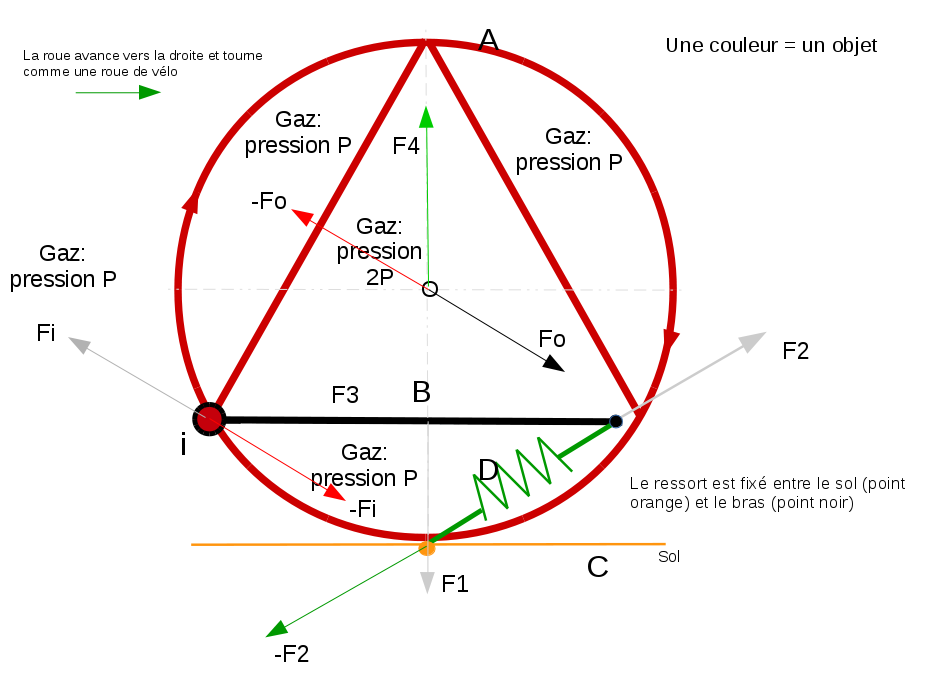
Et le moment reçu par la roue est de Fi*d = Fi*sqrt(3)/2*R , comme Fi=sqrt(3) le moment vaut 1.5R, c'est cela ? Le moment va ralentir la roue et la force Fo sur le centre va faire accélérer le centre de gravité.

[invite8e757dd6]

Bonjour,

Je reviens sur les forces, je voulais savoir si elles sont bien dessinées comme cela:



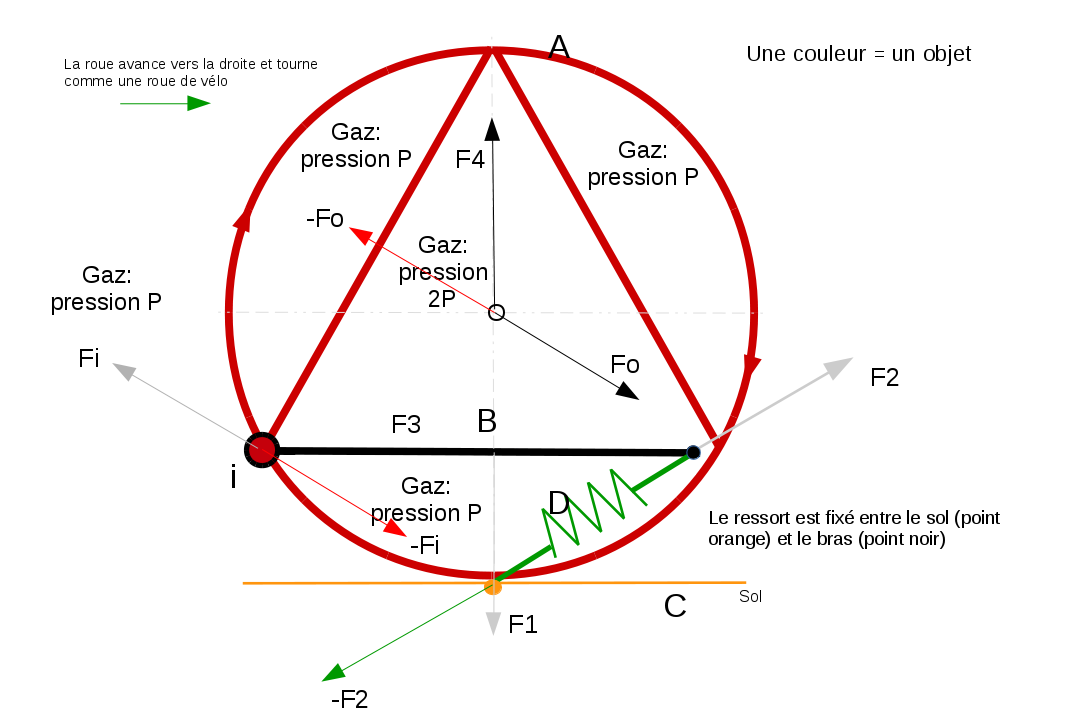
Les forces grises sont appliquées au bras noir
La force verte au sol
Les forces rouge à la roue (couple)
Les forces noires au centre de la roue

Avec rayon = 1 m, profondeur = 1m, P = 1 Pa
Chaque force vaut sqrt(3) N
Le couple sur la roue vaut 1.5 Nm

Sans frottement entre la roue et le sol.

a+

[invitef29758b5]

Les forces noires au centre de la roue

Il n' y a pas de force appliquée au centre de la roue pour la bonne raison qu' il n' y a rien au centre de la roue pour transmettre une force .

Le couple sur la roue vaut 1.5 Nm

La résultante n' étant pas nulle , ce n' est pas un couple et il faut donc préciser en quel point tu exprimes ce moment .

[invite8e757dd6]

Il n' y a pas de force appliquée au centre de la roue pour la bonne raison qu' il n' y a rien au centre de la roue pour transmettre une force.

Avec un vélo, je lance le vélo sur une route normale (avec friction) et ensuite j'arrive sur un revêtement sans friction, le vélo avance toujours, la roue tourne toujours, si j'applique la force avec le ressort sur un angle très faible, la force ne va pas être transmise au centre de la roue ?

La résultante n' étant pas nulle , ce n' est pas un couple et il faut donc préciser en quel point tu exprimes ce moment .

Sur le point qui se situe au centre de la roue

Merci pour votre aide

[invitef29758b5]

la force ne va pas être transmise au centre de la roue ?

Une force ne se transmet pas à "rien" .
Elle se transmet à un objet .
Dans le cas d' un vélo , les forces sur la roue se transmettent au moyeux via les rayons .

[invite8e757dd6]

Donc en ajoutant des rayons de la partie rouge vers le centre de la roue comme cela:



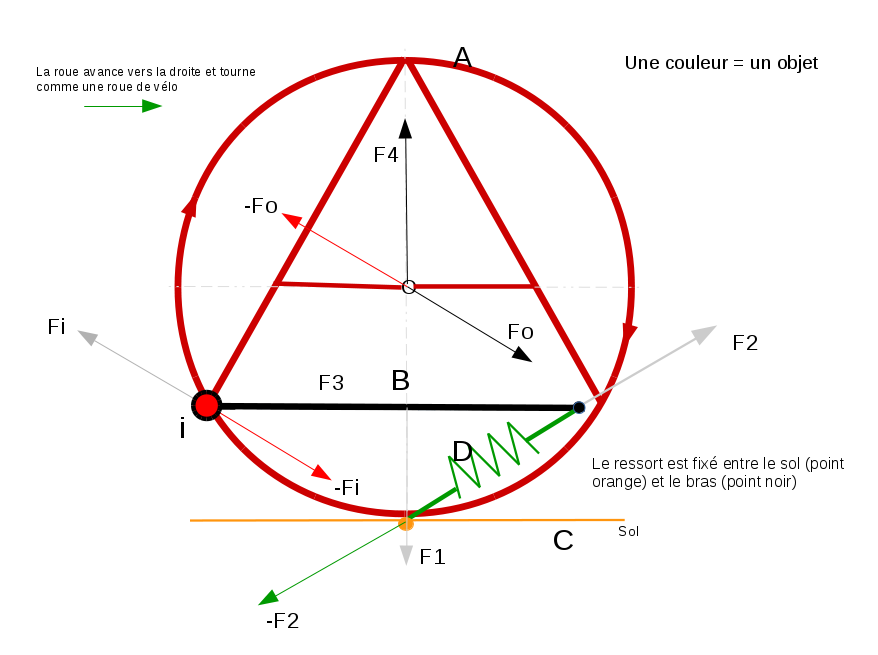
cela suffit à transmettre la force au centre ?

[invitef29758b5]

cela suffit à transmettre la force au centre ?

Le centre n' est pas un objet physique .

[invite8e757dd6]

Il faut que le centre possède une masse, c'est ça ?

[invitef29758b5]

Pas nécessairement .
Mais une force se transmet à un objet . Le centre n' est pas un objet , c' est une notion abstraite .

[invite8e757dd6]

Oui, mais je me demande ce qu'il faut pour que cette force existe. Si la roue est sur un vélo alors la force existe au centre de la roue ? Et qu'ensuite cette force est transmise au centre de masse du vélo ?

[antek]

Oui, mais je me demande ce qu'il faut pour que cette force existe. Si la roue est sur un vélo alors la force existe au centre de la roue ? Et qu'ensuite cette force est transmise au centre de masse du vélo ?

Je suppose qu'il faut une liaison mécanique !

[invite8e757dd6]

Bonjour,

Si la roue est sur un vélo comme une roue de vélo, la roue est bien en rotation autour du moyeu, non ?

a+

[antek]

Si la roue est sur un vélo comme une roue de vélo, la roue est bien en rotation autour du moyeu, non ?

Pardon, je n'avais pas vu le nouveau schéma #48 !

[invite51d17075]

@yy527:
quelle est maintenant ton exercice.?
s'agit il de savoir si et comment le ressort comprimé induirait une rotation ?
ou bien rajoutes tu simplement une rotation en questionnant sur une modification éventuelle de la situation statique étudiée actuellement?

[invite8e757dd6]

Au départ, la roue n'était en rien statique mais je sais plus qui a dit que c'était pareil. La roue roule vers la droite et tourne comme une roue de vélo, le centre de la roue a une masse ainsi que le pourtour, pour simplifier mon exercice j'avais pas indiqué que c'était sur un vélo.Pour faire simple, je roule en vélo sur du bithume et j'arrive sur un sol sans friction, une des roues du vélo est comme je l'ai dessiné, j'actionne le ressort sur un angle très faible, que se passe t-il, est ce que le vélo accèlère et la roue décélère ? Je souhaite savoir si le ressort (même sur un angle très faible) fournit un moment sur la roue et que le centre de la roue a bien une force nette provenant de l'action du ressort. D'après mon dessin, j'ai bien la somme des forces à zéro, donc ce n'est peut être pas faux. Je souhaite savoir si mes forces sont correctes.

Merci
a+

[invitef29758b5]

Oui, mais je me demande ce qu'il faut pour que cette force existe.

Pour qu' une force "existe" , il faut deux objets en interaction .
La roue agit sur le vélo au niveau du moyeux .

[invite51d17075]

la barre B agit sur A
le ressort agit sur A
est ce que les forces induites ont un moment par rapport au moyeu, et donc une influence sur la rotation ?

[invite8e757dd6]

Le ressort agit sur le sol et la barre B
La barre B agit sur la roue A à partir de l'axe i, il y a une force nette sur l'axe i
La roue étant reliée par le moyeu avec des rayons, elle transmet cette force au moyeu, donc la roue a une couple (forces en rouge) et le moyeu une force nette

Mais je n'en suis pas certain