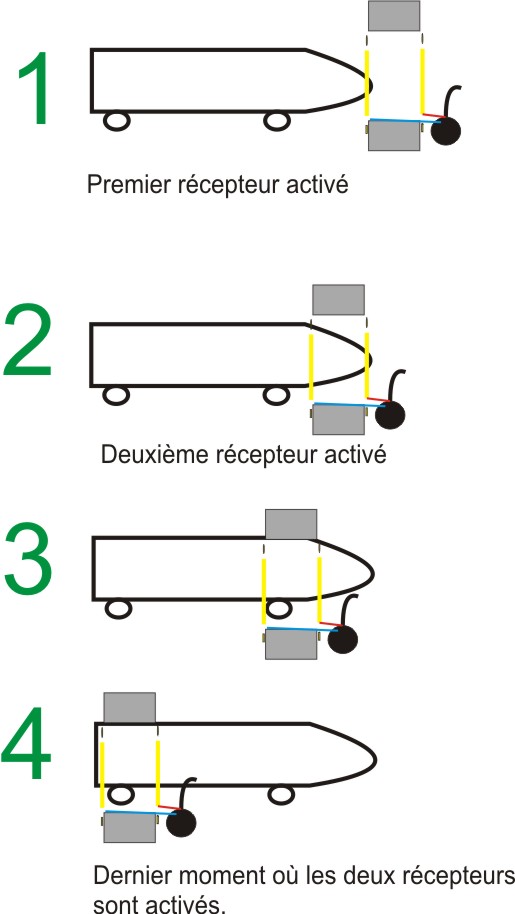
Merci pour tous ces calculs, mais je crois qu'ici, nous sommes aussi d'accord? c'est un autre problème, celui d'une analyse "optique", ceci vu d'un angle longitudinal par rapport au tunnel et au train. ....A ajouter dans le futur pdf !!!Perso, je dirais qu'il est vu plus long à bord du train que sur le quai, car le tunnel s'approche du train, il n'est pas vu de coté à bord du train !
Par l’expression « contraction des longueur et dilatation des durée », il y a tendance à penser que tous les objets en mouvement se contracte (d'apparence), et ce quel que soit la direction de son mouvement, on l’observerait toujours contracté … C’est faux ! à moins que je n'ai rien compris !
Un train qui s’éloigne parait plus court, plus sombre et tirant vers le rouge.
Un train qui s’approche parait plus long, plus lumineux et tirant vers le bleu.
L/gamma ne suffit pas pour décrire la longueur apparente (L’) d’un bolide, de longueur (L) lorsqu’il est au repos.
Par exemple, pour un bolide d’une longueur au repos (L) de 1 mètre et à 50% de la vitesse de la lumière :
Beta = v / c = 150 000 / 300 000 = 0,5 c
Gamma = 1 / √ (1 - Béta²) = 1 / √ (1 – 0,5²) = 1,155
Longueur apparente L’ = L / Gamma = L / 1,155 = 0,866 m
Je veux bien, mais à seule condition que nous l’observons à peu près à la perpendiculaire de sa trajectoire.
Il est préférable de faire :
Longueur apparente L’ = L / [ Gamma * (1 – Béta * Cos(angle)) ]
L’ = 1 / [ 1,155 * (1 – 0,5 * Cos(90)) ] = 0,866 m
Plus l’angle devient petit et plus la longueur apparente augmente (lorsqu'il s'éloigne l'angle est supérieur à 90°).
Ainsi, si l’angle devient assez petit, la longueur apparente du bolide en mouvement devient plus grande que s’il était au repos.
Si le bolide vient directement vers nous, disons à 90% de la vitesse de la lumière :
Sa longueur apparente n’est pas contractée d’une demi fois (0,435 m) mais dilaté de 4,35 fois
Beta = v / c = 270 000 / 300 000 = 0,9 c
Gamma = 1 / √ (1 - Béta²) = 1 / √ (1 – 0,9²) = 2,294
Longueur apparente L’ = L / [ Gamma * (1 – Béta * Cos(angle)) ]
L’ = 1 / [ 2,294 * (1 – 0,9 * Cos(0)) ] = 4,359 m
Ou bien pour faire plus simple,
Lorsque le bolide s’approche :
L’ = L * √ ((1 + Béta) / (1 – Béta))L’ = 1 * √ ((1 + 0,9) / (1 – 0,9)) = 4,359 m
Lorsque le bolide s’éloigne :
L’ = L * √ ((1 - Béta) / (1 + Béta))
L’ = 1 * √ ((1 - 0,9) / (1 + 0,9)) = 0,229 m
-----