Le paradoxe de la bombe dans le train en RR

[invite70335176]

Bonjour,
Sur wikipedia, alors que je lisais quelques articles sur la RR, je suis tombé sur le "paradoxe du train" où une bombe exploserait dans un référentiel mais pas dans l'autre. Le paradoxe est levé car il y a une petite embrouille dans l'énoncé qui ne permet pas finalement à un signal d'être acheminé assez rapidement de l'avant à l'arrière du train.
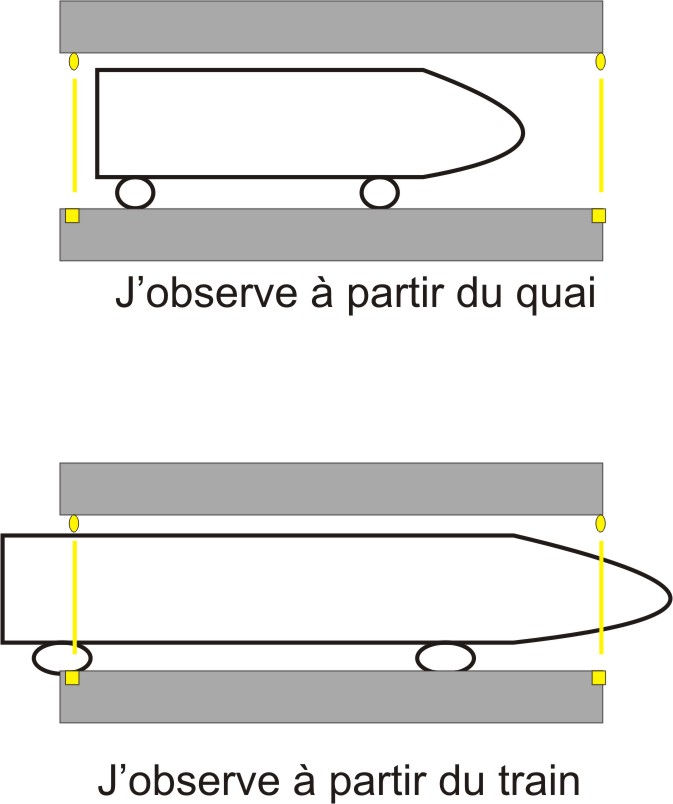
Je vous soumets donc un énoncé parallèle : voilà donc un train construit de façon à ce qu'il ait la même longueur qu'un tunnel, du moins avant qu'il n'ait à le traverser. Je place au plafonnier et au sol du tunnel deux émetteurs-détecteurs, un à l'avant, l'autre à l'arrière. Ces deux instruments sont programmés pour lancer à très grande fréquence un signal. On s'arrange sur notre référentiel du quai, que les signaux soient lancés à l'entrée et à la sortie du tunnel aux mêmes moments. On décide du fait que si les récepteurs au sol détectent au même moment un signal couplé, une bombe explose.
Moi - observateur au quai - je vois passer le train - disons à 1/2 c. Contraction de la longueur du train, donc, les deux récepteurs (à l'avant et à l'arrière du tunnel) ne sont jamais activés en même temps : pas d'explosion.
Toi - observateur dans le train - tu vois passer un tunnel à grande vitesse, donc il te parait plus court que ton train, donc ton train va faire déclencher les deux récepteurs au sol du tunnel, la bombe explose.

Comment peut-on résoudre cette apparente contradiction ? Merci

Ci-dessous, une copie d'écran d'une partie de l'expérience sur wiki
-----

[Lansberg]

Bonjour,

Moi - observateur au quai - je vois passer le train - disons à 1/2 c. Contraction de la longueur du train, donc, les deux récepteurs (à l'avant et à l'arrière du tunnel) ne sont jamais activés en même temps : pas d'explosion.
Toi - observateur dans le train - tu vois passer un tunnel à grande vitesse, donc il te parait plus court que ton train, donc ton train va faire déclencher les deux récepteurs au sol du tunnel, la bombe explose.

Les événements A et B ne sont pas simultanés, ni pour O, ni pour O', donc il n'y a pas d'explosion (revoir le diagramme d'espace-temps de wiki).

[invite70335176]

Bonjour,



Les événements A et B ne sont pas simultanés, ni pour O, ni pour O', donc il n'y a pas d'explosion (revoir le diagramme d'espace-temps de wiki).

Bonjour,
Dans l'expérience wiki, celle-ci est un peu différente, il faut que le signal arrive d'un côté à l'autre du train, ce qui permet d'éviter le paradoxe.
C'est pour cela que j'ai modifié les données. Ici, les émetteurs-détecteurs sont autonomes, indépendants du passage du train, émettent chaque "pico-seconde" un signal, et il me semble bien que du point de vue de l'observateur du train, celui-ci rentre dans un tunnel largement sous-dimensionné en longueur pour son train, et donc, je ne vois pas très bien comment empêcher les deux détecteurs d'envoyer un signal "positif" couplé. Je suppose bien que je me trompe, mais n'y a t-il pas moyen de me l'expliquer par une logique du même genre ? Merci.

[Lansberg]

Je ne vois pas comment ceci peut se produire : "On décide du fait que si les récepteurs au sol détectent au même moment un signal couplé, une bombe explose."

Pour O, la succession des événements est la suivante : L'avant du train "coupe" le signal du détecteur à l'entrée du tunnel ; L'arrière du train passe le détecteur à l'entrée du tunnel ; L'avant du train "coupe" le détecteur à la sortie du tunnel ; L'arrière du train passe ce détecteur.
Pour O' : L'avant du train "coupe" le détecteur à l'entrée du tunnel puis il coupe celui à la sortie du tunnel avant que l'arrière du train ne passe au niveau du détecteur à l'entrée du tunnel.

Si j'ai bien compris le fonctionnement du dispositif, je ne vois donc pas comment il pourrait y avoir simultanéité et donc un "signal couplé" !

[A voir en vidéo sur Futura]

[invite70335176]

Je ne vois pas comment ceci peut se produire : "On décide du fait que si les récepteurs au sol détectent au même moment un signal couplé, une bombe explose."

Pour O, la succession des événements est la suivante : L'avant du train "coupe" le signal du détecteur à l'entrée du tunnel ; L'arrière du train passe le détecteur à l'entrée du tunnel ; L'avant du train "coupe" le détecteur à la sortie du tunnel ; L'arrière du train passe ce détecteur.
Pour O' : L'avant du train "coupe" le détecteur à l'entrée du tunnel puis il coupe celui à la sortie du tunnel avant que l'arrière du train ne passe au niveau du détecteur à l'entrée du tunnel.

Si j'ai bien compris le fonctionnement du dispositif, je ne vois donc pas comment il pourrait y avoir simultanéité et donc un "signal couplé" !

Je me fais mal comprendre. Oublions l'expérience de wiki, ce sera plus simple. Dans mon expérience, il y a simplement deux capteurs à l'entrée et à la sortie du tunnel (donc pas d'interaction entre l'avant et l'arrière comme dans wiki). Je dis simplement : si les deux capteurs sont positifs en même temps (comme une porte ET en informatique), alors une bombe explose. Et donc : voilà un train qui est plus grand que le tunnel, donc forcément, les deux capteurs détectent (à plusieurs reprises par ailleurs puisque les émetteurs pulsent à chaque pico-seconde) l'occlusion, et....boum ! Ceci évidemment du point de vue du voyageur.

[Amanuensis]

Je ne vois pas comment ceci peut se produire : "On décide du fait que si les récepteurs au sol détectent au même moment un signal couplé, une bombe explose."

Très justement.

La réponse au "paradoxe" est simplement: cela ne peut pas se produire si la vitesse relative du train et du tunnel n'est pas nulle.

(La démo n'est pas bien difficile, elle dérive immédiatement de ce qui est expliqué dans le premier message: si les deux événements sont simultanés pour le tunnel, alors leur distance dans le référentiel où le tunnel est immobile est égal à la longueur du train, la même que dans le référentiel dans lequel le train est immobile, et cela n'est possible que si les deux référentiels coïncident (sur l'axe du tunnel) et donc que si le train a une vitesse nulle par rapport au tunnel (selon le même axe).

[Amanuensis]

Je me fais mal comprendre. Oublions l'expérience de wiki, ce sera plus simple. Dans mon expérience, il y a simplement deux capteurs à l'entrée et à la sortie du tunnel (donc pas d'interaction entre l'avant et l'arrière comme dans wiki). Je dis simplement : si les deux capteurs sont positifs en même temps (comme une porte ET en informatique), alors une bombe explose. Et donc : voilà un train qui est plus grand que le tunnel, donc forcément, les deux capteurs détectent (à plusieurs reprises par ailleurs puisque les émetteurs pulsent à chaque pico-seconde) l'occlusion, et....boum ! Ceci évidemment du point de vue du voyageur.

C'est plus clair. C'est une variante d'un "paradoxe classique" (comme le plus souvent...), celui d'une échelle et de portes de grange qu'on ferme. Exemple: Paradoxe 3 dans https://fr.wikipedia.org/wiki/Petite...de_pens%C3%A9e

Ce qui est vu comme "simultané" par les occupants du train (les détecteurs positifs en même temps) ne l'est pas pour le tunnel (donc la conclusion qu'il y aura explosion n'est pas justifiée).

[phys4]

Je ne vois pas d'aléa sur la décision : il faut savoir si les détecteurs voient un train en même temps.
Qui décide que le train est visible des deux cotés à la fois, le corrélateur est-il sur le quai ou dans le train ?

S'il est sur le quai il n'y a pas coïncidence, s'il est dans le train il y coïncidence : cela n'entraine pas de contradiction, car la position du corrélateur est déterminée, il ne peut pas être dans les deux à la fois.
Votre énoncé n'est pas bien rédigé, mais je crois avoir compris ce que vous vouliez dire.

[Lansberg]

il y a simplement deux capteurs à l'entrée et à la sortie du tunnel (donc pas d'interaction entre l'avant et l'arrière comme dans wiki). Je dis simplement : si les deux capteurs sont positifs en même temps (comme une porte ET en informatique), alors une bombe explose.

S'il n'y a pas d'interaction comment définir "deux capteurs positifs en même temps" ,

[invite70335176]

S'il n'y a pas d'interaction comment définir "deux capteurs positifs en même temps" ,

Voici donc un schéma pour être certain qu'on se comprenne bien.


Je rappelle : les deux faisceaux sont pulsés à partir du référentiel du quai. Il suffise que les deux capteurs soient positifs tous les deux pour déclencher la bombe. Dans le référentiel du quai, le train est raccourci, donc n'actionne jamais en même temps les deux capteurs. Dans le référentiel du voyageur, le tunnel est raccourci, donc, les deux capteurs sont positifs, la bombe explose.

[Amanuensis]

Je répète, ce n'est qu'une variante du grand classique "échelle dans grange".

Quel intérêt de reposer autrement?

Quel intérêt de discuter une fois de plus un des "grands classiques"?

En plus, les "explications" sont toujours les mêmes, et reviennent à réexpliquer encore et encore les bases de la RR, en particulier l'absence de simultanéité absolue, et en particulier le soin qu'il faut prendre dans tout intitulé de "paradoxe" à ne pas mélanger des "simultanéités".

[invite70335176]

Je répète, ce n'est qu'une variante du grand classique "échelle dans grange".

Quel intérêt de reposer autrement?

Quel intérêt de discuter une fois de plus un des "grands classiques"?

En plus, les "explications" sont toujours les mêmes, et reviennent à réexpliquer encore et encore les bases de la RR, en particulier l'absence de simultanéité absolue, et en particulier le soin qu'il faut prendre dans tout intitulé de "paradoxe" à ne pas mélanger des "simultanéités".

Et dans le même temps, cela montre à quel point ce phénomène est mal expliqué aux gens. Il n'y a qu'à voir dans Wikipédia au sujet du pseudo faux paradoxe de Langevin (ou je ne sais pas comment il faut le nommer) le résumé des interprétations contradictoires qui en sont faites, avec un désaccord même parmi les scientifiques.

Dans mon exemple, oui ou non, il y a t-il contraction des longueurs du tunnel pour le voyageur ? Et si ce n'est pas une illusion, comme je pense le prétend la théorie de la RR, les deux capteurs sont positifs pendant un bon moment, au contraire de l'autre point de vue.

Si au moins, ne fut-ce qu'une fois pour toutes, un exposé clair qui fasse l'unanimité soit exposé, cela éviterait les sempiternelles mêmes questions. Il suffirait d'un seul bon pdf, si vous le connaissez, je serai ravi d'en prendre connaissance. Sauf si vous me dites qu'il faille accepter les conclusions de mathématiques compliquées, ce sera alors un gros gain de temps.

[phys4]

En suivant votre dessin, les capteurs sont sur le quai, donc leur simultanéité est testé du quai.
Par conséquent, ils ne voient jamais le train simultanément, c'est tout.

Le point de vue du voyageur n'intervient pas. Il peut au plus en conclure que le système de synchronisation du quai est déréglé, s'il ne connait pas la RR.

[Amanuensis]

Et dans le même temps, cela montre à quel point ce phénomène est mal expliqué aux gens.

Je ne pense pas. Il y a tellement d'explications qu'on peut trouver sur le net que dire qu'il est mal expliqué ne peut pas expliquer le retour systématique des mêmes questions.

Pour moi c'est simplement que c'est contre-intuitif et qu'une majorité n'arrive pas à passer outre leur intuition (aussi appelée par certains "bon sens").

Il n'y a qu'à voir dans Wikipédia au sujet du pseudo faux paradoxe de Langevin (ou je ne sais pas comment il faut le nommer) le résumé des interprétations contradictoires qui en sont faites, avec un désaccord même parmi les scientifiques.

?? Il n'y a pas de désaccord parmi les scientifiques. Ceux qui colportent cela sont ceux qui sont restés à leur intuition, à leur "bon sens".

[Le site en français n'est pas vraiment de la physique, plutôt du bla-bla autour de l'histoire du soi-disant paradoxe. L'article en anglais est à préférer, de loin.]

Dans mon exemple, oui ou non, il y a t-il contraction des longueurs du tunnel pour le voyageur ?

Oui, et alors?

Et si ce n'est pas une illusion, comme je pense le prétend la théorie de la RR

Si vous le pensez, que discuter??

, les deux capteurs sont positifs pendant un bon moment, au contraire de l'autre point de vue.

Cela n'implique en rien qu'ils le soient à un quelconque instant "en même temps"au sens du référentiel du tunnel.

Si au moins, ne fut-ce qu'une fois pour toutes, un exposé clair qui fasse l'unanimité soit exposé, cela éviterait les sempiternelles mêmes questions.

Une fois que vous aurez compris, vous pourrez proposer cet exposé clair. Il le sera pour vous. Qu'il fasse l'unanimité restera à démontrer.

Il suffirait d'un seul bon pdf, si vous le connaissez, je serai ravi d'en prendre connaissance. Sauf si vous me dites qu'il faille accepter les conclusions de mathématiques compliquées, ce sera alors un gros gain de temps.

Ce n'est pas une question de maths, mais des bases erronées au "bon sens". Pendant des siècles l'idée d'une simultanéité absolue "allait de soi", étant une "évidence". On sait maintenant que c'était un postulat, et que ce postulat est réfuté par les observations (1). Tant que cela n'est pas compris, tant que quelqu'un reste sur les "raisonnements de bon sens" basés, consciemment ou non, sur l'idée de simultanéité absolue, aucune explication ne lui sera claire.

Une conséquence simple du refus de la simultanéité absolue est les précautions à prendre quand on emploie une expression comme "en même temps". Votre dernière intervention montre que la précaution n'est pas prise dans "donc n'actionne jamais en même temps les deux capteurs". Ergo, vous raisonnez inconsciemment avec une simultanée absolue, et aucune explication ne vous sera claire.

(1) Et les divers soi-disant "paradoxes" ne sont à bien regarder que des illustrations de ce qu'il se passe quand on rejette le postulat, des expériences de pensée qui justement le réfute. Le seul "paradoxe" est que le postulat reste valable dans l'inconscient de tant de gens.

[invite70335176]

Pour moi c'est simplement que c'est contre-intuitif et qu'une majorité n'arrive pas à passer outre leur intuition (aussi appelée par certains "bon sens").





Cela n'implique en rien qu'ils le soient à un quelconque instant "en même temps"au sens du référentiel du tunnel.






Une conséquence simple du refus de la simultanéité absolue est les précautions à prendre quand on emploie une expression comme "en même temps". Votre dernière intervention montre que la précaution n'est pas prise dans "donc n'actionne jamais en même temps les deux capteurs". Ergo, vous raisonnez inconsciemment avec une simultanée absolue, et aucune explication ne vous sera claire.

(1) Et les divers soi-disant "paradoxes" ne sont à bien regarder que des illustrations de ce qu'il se passe quand on rejette le postulat, des expériences de pensée qui justement le réfute. Le seul "paradoxe" est que le postulat reste valable dans l'inconscient de tant de gens.

Mais je suis d'accord avec vous sur l'atteinte au bon sens.
Je comprends tout à fait nos ancêtres lorsqu'ils pensaient que la Terre était plate ! C'est évident, puisqu'ils constataient qu'ils avaient un poids, ils pensaient qu'ils tomberaient dès lors qu'ils s'aventureraient sur une courbe. Mais lorsque Newton est venu avec sa gravitation et l'attraction entre les masses, tout devenait aussi cohérent (malgré qu'il se trompait d'une certaine façon). Si l'on accepte cette attraction des masses, l'intuition évolue et on accepte les nouvelles données. Puis vient notre génie Einstein, qui change à nouveau l'intuition en remplaçant l'attraction des masses, par une courbure de l'espace-temps provoquée par les masses. Ses calculs lui donnent une précision inégalée, mais il semble lui-même admettre qu'une nouvelle intuition remplacera la sienne dans le futur.
Pour ma part, je ne doute pas que mon intuition est faussée et je prétends qu'elle est faussée pour tout le monde. Vous avez déjà donné votre opinion là-dessus, mais tant que nous n'aurons pas de "solution globale" à notre univers, il faut admettre que notre intuition même mise à jour n'est pas encore la bonne.
Mais pour revenir à mon expérience, la non simultanéité, oui, je croyais que je l'avais comprise, mais je ne vois pas ce qu'elle vient faire dans mon exemple. Ici, ce n'est pas - à mon sens- un problème de simultanéité, mais cela concerne le postulat que les longueurs se contractent lorsqu'un objet est en mouvement. La RR nous dit que le tunnel est raccourci pour le voyageur, donc son train allume bien les deux capteurs (peu importe si ce n'est pas au même moment puisque je postule qu'il suffise que les deux capteurs soient positifs, or manifestement, il me semble (toujours) que c'est le cas un certain temps.
Vous voulez dire que mon schéma (celui du dessous) n'est pas conforme à la réalité ? Merci de votre patience.

[Amanuensis]

Mais pour revenir à mon expérience, la non simultanéité, oui, je croyais que je l'avais comprise, mais je ne vois pas ce qu'elle vient faire dans mon exemple.

Pourtant cela a été indiqué pratiquement dans toutes les réponses, par différents participants. J'imagine qu'elles n'ont pas été "assez claires". Mais je ne vois pas comment faire mieux.

Ici, ce n'est pas - à mon sens- un problème de simultanéité

Les autres participants pensent le contraire.

, mais cela concerne le postulat que les longueurs se contractent lorsqu'un objet est en mouvement.

Comment définissez-vous la "longueur" d'un objet, selon un observateur quelconque?

[Indice: tout ce que vous proposerez fera intervenir implicitement ou explicitement une notion de simultanéité.]

[phys4]

Vous voulez dire que mon schéma (celui du dessous) n'est pas conforme à la réalité ? Merci de votre patience.

Vous avez deux schémas différents, c'est donc que vous admettez qu'il y a deux points de vue distincts.

Vos schémas sont bien conformes, mais il faut améliorer votre raisonnement : vous mettez les capteurs sur le quai, c'est donc par rapport au quai qu'il faut tester leur coïncidence ?

[Amanuensis]

Comment définissez-vous la "longueur" d'un objet, selon un observateur quelconque?

Je me suis mal exprimé. La notion de longueur d'un objet pose le problème de la notion d'objet. La question est à remplacer par

"Comme définissez-vous la distance entre deux événements, selon un observateur quelconque?"

[invite70335176]

Bien. Nous sommes d'accord sur le point de vue du quai.
Pour le voyageur maintenant : lorsqu'il est parti d'une autre gare à vitesse "normale", sa longueur (disons 100 mètres à vitesse classique) a la même longueur que le tunnel qu'il rencontrera plus loin. Lorsqu'il aura atteint une vitesse se rapprochant de C au moment d'arriver à ce fameux tunnel, la RR dit que la longueur de ce tunnel vaudra (puisqu'il considère que c'est le tunnel qui va vers lui), disons 50 mètres. Donc, il remplit bien tout le tunnel, non ? Je me trompe mais où ? Encore merci de votre patience, il est possible qu'il me faille prendre tout simplement quelques vacances pour mettre mon cerveau au repos, expliquant qu'il coince ainsi.

[invite70335176]

Comment définissez-vous la "longueur" d'un objet, selon un observateur quelconque?

[Indice: tout ce que vous proposerez fera intervenir implicitement ou explicitement une notion de simultanéité.]

Mais ai-je besoin d'une définition de longueur dans mon exemple ? On me certifie à moi voyageur, que le tunnel est devenu plus court, donc mon train remplit ce tunnel entièrement (et du même coup les détecteurs sont activés), peu importe s'ils sont activés simultanément, le fait est qu'ils sont activés tous les deux quand le train le déborde de part et d'autre.
Je dois encore une fois coincer bêtement sur quelque chose d'évident. Je m'en veux, mais ça ne me saute pas aux yeux.

[Lansberg]

Bien. Nous sommes d'accord sur le point de vue du quai.

Pas forcément ! Il y a plusieurs possibilités. Il faudrait une situation précise : longueur du tunnel, longueur du train, vitesse.

[PPathfindeRR]

Bonjour,

Elle est bizarre cette expérience de pensé ! à quoi elle rime ?!

Un tunnel qui s'approche n'apparait pas plus court mais plus long !

La contraction de longueur (dans le sens de son mouvement) va dépendre aussi de l'angle sous lequel sa direction est par rapport à nous !

[coussin]

Comme souligné par Amanuensis, c'est l'échelle et la grange. Problème discuté et expliqué à foison un peu partout.
Donc, peut-être commencer par lire et digérer ces explications et revenir avec une question précise ?

[phys4]

Pour le voyageur maintenant : lorsqu'il est parti d'une autre gare à vitesse "normale", sa longueur (disons 100 mètres à vitesse classique) a la même longueur que le tunnel qu'il rencontrera plus loin. Lorsqu'il aura atteint une vitesse se rapprochant de C au moment d'arriver à ce fameux tunnel, la RR dit que la longueur de ce tunnel vaudra (puisqu'il considère que c'est le tunnel qui va vers lui), disons 50 mètres. Donc, il remplit bien tout le tunnel, non ? Je me trompe mais où ?

Non, vous ne vous trompez pas, mais où est donc l'anomalie?
il n'y en a pas tout simplement. Le voyageur a bien le droit d'avoir un point de vue différent de celui du chef de gare!

Je n'arrive pas à voir ce qui coince chez vous, sauf peut être cette histoire de simultanéité implicite ?

[Amanuensis]

Mais ai-je besoin d'une définition de longueur dans mon exemple ?

Ben oui. Et c'est même essentiel.

On me certifie à moi voyageur, que le tunnel est devenu plus court

Bien une question de longueur, ça ; non?

il remplit bien tout le tunnel, non ?

Encore une réflexion qui sous-tend une idée sur les longueurs et distances.

Je m'en veux, mais ça ne me saute pas aux yeux.

Ces exemples devraient appeler à réfléchir sur les notions de simultanéité et de distance spatiale entre événements.

[invite70335176]

Non, vous ne vous trompez pas, mais où est donc l'anomalie?
il n'y en a pas tout simplement. Le voyageur a bien le droit d'avoir un point de vue différent de celui du chef de gare!

Je n'arrive pas à voir ce qui coince chez vous, sauf peut être cette histoire de simultanéité implicite ?

Que les points de vue soient différents, je l'accepte volontiers. Le problème, c'est que dans un des deux cas, il y a une bombe qui explose.

Mais je ne voudrais pas vous embêter trop longtemps avec ça, puisqu'apparemment je coince. et je vais suivre le conseil d'Amanuensis et d'essayer de trouver les articles traitant de l'échelle et de la grange.
Pour aller point par point, dites-moi : le tunnel, du point de vue du voyageur, s'il était bien de même longueur lorsqu'il était au repos, à présent que ce voyageur est à 2/3 de c, le tunnel, pour lui, est bien beaucoup plus court que son train ? Ce n'est pas une illusion, ou si ? (parce qu'alors, je comprends bien entendu). Son train déborde de part et d'autre du tunnel à un instant t, sur cela, on est d'accord ?

[phys4]

Que les points de vue soient différents, je l'accepte volontiers. Le problème, c'est que dans un des deux cas, il y a une bombe qui explose.

Pour aller point par point, dites-moi : le tunnel, du point de vue du voyageur, s'il était bien de même longueur lorsqu'il était au repos, à présent que ce voyageur est à 2/3 de c, le tunnel, pour lui, est bien beaucoup plus court que son train ? Ce n'est pas une illusion, ou si ? (parce qu'alors, je comprends bien entendu). Son train déborde de part et d'autre du tunnel à un instant t, sur cela, on est d'accord ?

Nous sommes d'accord, sauf sur un point : la bombe n'explose pas, parce que vous avez mis le déclencheur sur le quai, c'est donc le point de vue du quai qui prévaut.
Vousne pouvez pas mettre le déclencheur des deux cotés à la fois. Il faut préciser votre schéma si vous voulez que l'on comprenne votre point de vue.

[PPathfindeRR]

le tunnel, pour lui, est bien beaucoup plus court que son train ? Ce n'est pas une illusion, ou si ?

Perso, je dirais qu'il est vu plus long à bord du train que sur le quai, car le tunnel s'approche du train, il n'est pas vu de coté à bord du train !

Par l’expression « contraction des longueur et dilatation des durée », il y a tendance à penser que tous les objets en mouvement se contracte (d'apparence), et ce quel que soit la direction de son mouvement, on l’observerait toujours contracté … C’est faux ! à moins que je n'ai rien compris !

Un train qui s’éloigne parait plus court, plus sombre et tirant vers le rouge.
Un train qui s’approche parait plus long, plus lumineux et tirant vers le bleu.

L/gamma ne suffit pas pour décrire la longueur apparente (L’) d’un bolide, de longueur (L) lorsqu’il est au repos.

Par exemple, pour un bolide d’une longueur au repos (L) de 1 mètre et à 50% de la vitesse de la lumière :

Beta = v / c = 150 000 / 300 000 = 0,5 c
Gamma = 1 / √ (1 - Béta²) = 1 / √ (1 – 0,5²) = 1,155

Longueur apparente L’ = L / Gamma = L / 1,155 = 0,866 m

Je veux bien, mais à seule condition que nous l’observons à peu près à la perpendiculaire de sa trajectoire.
Il est préférable de faire :

Longueur apparente L’ = L / [ Gamma * (1 – Béta * Cos(angle)) ]

L’ = 1 / [ 1,155 * (1 – 0,5 * Cos(90)) ] = 0,866 m

Plus l’angle devient petit et plus la longueur apparente augmente (lorsqu'il s'éloigne l'angle est supérieur à 90°).
Ainsi, si l’angle devient assez petit, la longueur apparente du bolide en mouvement devient plus grande que s’il était au repos.

Si le bolide vient directement vers nous, disons à 90% de la vitesse de la lumière :

Sa longueur apparente n’est pas contractée d’une demi fois (0,435 m) mais dilaté de 4,35 fois

Beta = v / c = 270 000 / 300 000 = 0,9 c
Gamma = 1 / √ (1 - Béta²) = 1 / √ (1 – 0,9²) = 2,294

Longueur apparente L’ = L / [ Gamma * (1 – Béta * Cos(angle)) ]

L’ = 1 / [ 2,294 * (1 – 0,9 * Cos(0)) ] = 4,359 m

Ou bien pour faire plus simple,

Lorsque le bolide s’approche :

L’ = L * √ ((1 + Béta) / (1 – Béta))

L’ = 1 * √ ((1 + 0,9) / (1 – 0,9)) = 4,359 m

Lorsque le bolide s’éloigne :

L’ = L * √ ((1 - Béta) / (1 + Béta))

L’ = 1 * √ ((1 - 0,9) / (1 + 0,9)) = 0,229 m

[invite70335176]

Nous sommes d'accord, sauf sur un point : la bombe n'explose pas, parce que vous avez mis le déclencheur sur le quai, c'est donc le point de vue du quai qui prévaut.
Vousne pouvez pas mettre le déclencheur des deux cotés à la fois. Il faut préciser votre schéma si vous voulez que l'on comprenne votre point de vue.

Très bien, et merci encore de me répondre. Je finirai par comprendre !
Je pense que vous avez bien compris mon schéma (mais je veux bien le préciser et le refaire plus finement). Sur le quai, deux détecteurs sont situés, un à l'avant, l'autre à l'arrière. Si un détecteur est activé alors que l'autre l'est déjà : boum !
Point de vue du quai : on ne discute pas, nous sommes d'accord.
Point de vue du voyageur : vous dites " c'est le point de vue du quai qui prévaut". C'est juste cela que je ne comprends pas. Le voyageur voit le tunnel plus court que son train. Mais, vous êtes d'accord, ce n'est pas une illusion pour lui, c'est réellement le cas ?
Si vous êtes d'accord, ce voyageur sait que son train, plus grand que le tunnel, aura lors de son passage ses deux récepteurs activés, et boum ! non?

J'ai suivi ainsi sur YouTube un prof qui fait un cours de la RR à ses élèves, et il prend l'exemple d'une règle qui est trop courte pour entrer dans une boite. Il explique : si je déplace cette règle à une vitesse sub-luminique, elle pourrait lors de son passage au-dessus de la boite restée dans le référentiel "immobile", rentrer dans cette boite, et ferait "sauter" cette boite, si sa vitesse redeviendrait classique. Faux aussi ?
Et j'insiste : mille fois merci.

[invite70335176]

Perso, je dirais qu'il est vu plus long à bord du train que sur le quai, car le tunnel s'approche du train, il n'est pas vu de coté à bord du train !

Bien vu ! c'est effectivement une bonne remarque, et donc bien à préciser lors de la formulation du problème.