Calcul des forces de réactions

[kanamuri]

Bonjour,

Est ce que quelqu'un pourrait me donner le calcul du détail des réactions Ra, Rb et Rc ?

Merci.
-----

[kanamuri]

personne pour une aide ?

[le_STI]

Salut.

Tu pourrais déjà simplifier le problème en considérant une poutre encastrée en B avec un appui en C (grâce à la symétrie).

[kanamuri]

ce qui donne ?

[A voir en vidéo sur Futura]

[Tifoc]

Bonsoir,
Ca ne donne rien vu qu'il n'y a aucune donnée (et le problème n'est pas symétrique).

[kanamuri]

Bonjour voila

[harmoniciste]

Bonjour,

Si la poutre est infiniment rigide, la répartition est indéterminable (systême hyperstatique):
Soit les deux supports extérieurs prennent toute la charge sans que la poutre appuie sur le support central,
soit elle appuie en totalité sur le support central, les deux autres étant totalement délestés.
soit un mix intermédiaire.
Dans la pratique, la poutre se déforme sous l'effet de la charge uniforme et il conviendrait probablement de connaitre sa raideur.

[kanamuri]

LA SOMME DES FORCES = 0 donc
Ra + Rb + Rc - w(2xl1+2xl2) = 0 et on voit directement que Ra = Rc (symétrie)
Rb = 2.w(l1+l2) - 2Ra

Le but étant de déterminer Ra à présent : (mais c'est ce passage là que j'arrive pas)
Ensuite la somme des moments au premier point est nulle
Donc Ra.l1+Rb.(l1+l2)+Rc.(l1+2l2)-w(2xl1+2xl2)^2=0 (est ce que la deuxième équation est juste ???)

[harmoniciste]

Bonjour,
Votre deuxième équation ne correspond pas à la somme des couples autour de A:
Elle semble plutôt s'appliquer à l'extrémité de la poutre.

[harmoniciste]

Vous ne semblez pas prendre ma première remarque en compte: Si la barre est indéformable, le systême est hyperstatique et la répartition de la charge en fonction de L1 et L2 n'est pas unique, mais indéterminée.
En conséquence, si la raideur (déformée) de la poutre n'est pas prise en compte, vous ne trouverez pas une loi de répartition unique en fonction de L₁/L₂.
A mon avis, il n'y a que deux répartitions communes à toute les raideurs de poutre:
Rb = 0 quand L₁ = L₂
Et Rb = 2 Ra quand L₁ = 0

[kanamuri]

c'est du bois

[kanamuri]

oui je sais qu elle s applique a l extrémité mais cette équation me donne rien ...

[le_STI]

Pour moi il s'agit "simplement" d'un problème de poutre sur trois appuis (RDM).

Fais des recherches sur le forum, ce sujet a forcément déjà été traité.

[harmoniciste]

Bonjour STI,
Quand L1 > L2, il n'y aura déjà plus que 2 appuis, vu la déformation élastique de la poutre.
Quand L1 = L2 le point central n'appuie plus que de 0 N
Quand L1< L2 l'appui sur le point central dépend de la raideur de la poutre

Avec une poutre rigoureusement indéformable, la répartition ne peut pas être définie (système hyperstatique)

[invite26498794]

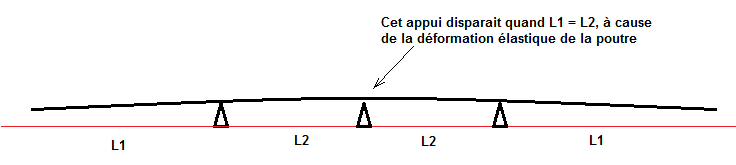
Simple problème de résistance de calcul d'appuis

Somme de forces = 0 et moments des forces par rapport à un point = 0

je fais le calcul ce soir si j'ai le temps.

[invite26498794]

bon je suis de retour et en regardant convenablement (j'avais lu trop vite), il s'agit bien d'une poutre hyperstatique de degré 1

il y a 3 inconnue à calculer et seulement deux équations de disponible (la somme des forces suivant x est non compté) donc il est impossible de créer un système d'équation pour résoudre le problème.

il faut donc passer par d'autres méthodes plus complexe pour résoudre le problème. Une recherche sur internet montre de toute façon à chaque fois la même réponse.

harmoniciste a raison