Tenseur de Riemann

[geometrodynamics_of_QFT]

Bonjour,

j'aimerais qu'on me convainque que l'approximation (canonique) suivante est sans conséquence pour la Cosmologie (et pour la RG en général)

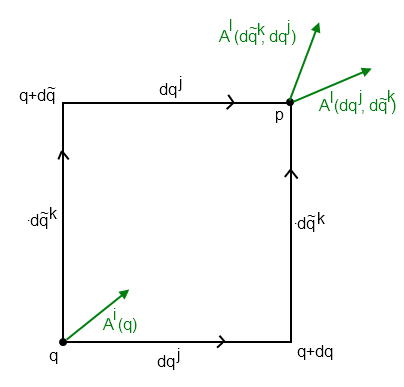
Dans mon cours de Relativité Générale, on calcule le transport parallèle d'un vecteur d'un point à un point sur une variété affine bidimensionnelle courbe, le long de deux chemins différents.
On peut donc le transporter parallèlement de à puis ensuite de à , ou alors le transporter d'abord de à et ensuite de à à (voir image attachée).



Soient et les composantes d'un vecteur exprimées dans le système de coordonnées associé à l'espace tangent au point et de la variété, respectivement.
Sachant que pour un transport parallèle, on a
où est la connexion linéaire.

On désire donc calculer

Calculons par exemple , le vecteur transporté parallèlement de à et ensuite à :





où on a utilisé .

En faisant de même pour , et en soustrayant les deux résultats, on obtient donc
.

Mon scepticisme vient d'ici:
On voit qu'on a négligé les termes d'ordre 2 en et dans l'expression de (le terme ), et pareil pour

Par conséquent, ne manque-t-il pas deux termes dans l'expression du tenseur de Riemann? Ne devrait-on pas écrire, pour gagner en précision:

?

Ou plutôt, écrire:
? Dans ce cas, comment écrire explicitement ce tenseur ?

Ma question principale est :
Etant donné que, par exemple, l'accélération de l'expansion de l'Univers est du second ordre en la métrique, et que le tenseur d'Einstein est construit à partir du tenseur de Riemann (dont on voit ici qu'il n'est qu'approximatif), ne pourrait-on pas envisager que les termes du second ordre négligés dans le développement ici pourraient avoir une influence sur, par exemple, les équations de Friedmann-Lemaître?

Je vous remercie d'avance pour vos interventions et justifications!
-----

[Amanuensis]

On cherche une expression tensorielle, c'est à dire une linéarisation. Les relations linéaires sont au premier ordre, sans termes du second ordre.

Le calcul est un calcul approximatif qu'il faut de toutes manières faire tendre vers la «limite» quand les deltas «tendent vers 0» et on postule à l'avance (et vérifie à la fin) que les termes du deuxième ordre sont dominés par des termes du premier ordre non nuls, et donc disparaissent au passage à la limite.

Si on voulait exprimer le deuxième ordre, on introduirait un tenseur supplémentaire sans changer le tenseur de Riemann. À comparer avec la dérivée première d'une fonction (linéarisation de la fonction) et la dérivée seconde (terme supplémentaire) si on veut gérer le deuxième ordre.

---

Au passage, selon mes réminiscences (à confirmer), la principale «approximation» consiste à affirmer que le point p est le même selon les deux chemins. C'est une «erreur» bien plus sérieuse que les termes du second degré dans une telle démonstration.

[geometrodynamics_of_QFT]

Merci pour votre réponse.
Ce n'est malheureusement pas encore clair pour moi :-/

On cherche une expression tensorielle, c'est à dire une linéarisation. Les relations linéaires sont au premier ordre, sans termes du second ordre.

Le calcul est un calcul approximatif qu'il faut de toutes manières faire tendre vers la «limite» quand les deltas «tendent vers 0» et on postule à l'avance (et vérifie à la fin) que les termes du deuxième ordre sont dominés par des termes du premier ordre non nuls, et donc disparaissent au passage à la limite.

Mais justement, ici comment montrer explicitement que ces termes sont négligeables?
Quand on regarde le tenseur de Riemann, on voit qu'on a des termes "dérivées de la connexion" (les deux premiers termes), des termes "produit de la connexion" (les deux derniers termes)...
Alors des termes croisés (dérivée de la connexion X connexion, càd le terme négligé dont je parle dans le message) ne sont-il pas aussi importants?

Si on voulait exprimer le deuxième ordre, on introduirait un tenseur supplémentaire sans changer le tenseur de Riemann. À comparer avec la dérivée première d'une fonction (linéarisation de la fonction) et la dérivée seconde (terme supplémentaire) si on veut gérer le deuxième ordre.

Justement, ici les termes supplémentaires apparaissent quand on développe au premier ordre la connexion au point q+dq.
Et la dernière équation que j'ai écrite exprime justement ce tenseur S à 6 indices qui rend la relation linéaire.

Au passage, selon mes réminiscences (à confirmer), la principale «approximation» consiste à affirmer que le point p est le même selon les deux chemins. C'est une «erreur» bien plus sérieuse que les termes du second degré dans une telle démonstration.

Mais, justement je voyais ça autrement :
On fixe un point p sur la variété, et on le rejoint par deux chemins différents. Donc forcément, le point p est le même selon les deux chemins?

[Amanuensis]

Mais justement, ici comment montrer explicitement que ces termes sont négligeables?

Comme dans tout passage à la limite en analyse: si ε tend vers 0, alors ε² est négligeable devant ε.

Quand on regarde le tenseur de Riemann, on voit qu'on a des termes "dérivées de la connexion" (les deux premiers termes), des termes "produit de la connexion" (les deux derniers termes)...
Alors des termes croisés (dérivée de la connexion X connexion, càd le terme négligé dont je parle dans le message) ne sont-il pas aussi importants?

Ce qui permet de négliger ou non sont les expressions en (dq)² ou (dq~)², pas leurs coefficients.

Justement, ici les termes supplémentaires apparaissent quand on développe au premier ordre la connexion au point q+dq.
Et la dernière équation que j'ai écrite exprime justement ce tenseur S à 6 indices qui rend la relation linéaire.

L'avant dernière formule dans le message #1 ne peut pas être correcte, on ne peut pas mettre des infinitésimaux tendant vers 0 dans le coefficient limite quand ces infinitésimaux tendent vers 0. Ce serait comme mettre un dt dans la valeur de la dérivée df/dt.

Le tenseur est une application bilinéaire applicable à dq dq~, il ne peut pas contenir des termes en en dq ou dq~.

On fixe un point p sur la variété, et on le rejoint par deux chemins différents. Donc forcément, le point p est le même selon les deux chemins?

Le problème est qu'on ne prend pas deux chemins quelconques, mais deux chemins qu'on va pouvoir décrire comme définis par une paire de vecteurs infinitésimaux, ce qui est nécessaire pour linéariser le commutateur.
On prend deux déplacements vectoriels dq et dq~ pour faire le premier chemin, soit (q+dq) +dq~ = p. Jusque là pas de problème. Mais quel est l'autre chemin? Ce serait le vecteur joignant q+dq~ à p ; pourquoi serait-il égal à dq? Il ne l'est pas nécessairement, et donc on doit écrire le second chemin comme ((q+dq~) + dq) + w) et faudrait exprimer w en fonction de dq et dq~, et le prendre en compte dans le calcul.

[A voir en vidéo sur Futura]

[azizovsky]

une lecture en diagonale (après la peinture ....), pour passer de q à q+dq , tu a fait une dérivée covariante D(q) et pour passer de q+dq une autre dérivée covariante, or il faut une dérivé covariante de D(q), càd D(q~)[D(q)].

ps: c'est le commutateur D(q~)D(q) - D(q)D(q~) qui donne le tenseur de courbure.