Rotation de Wick : opérateur expérimental

[stefjm]

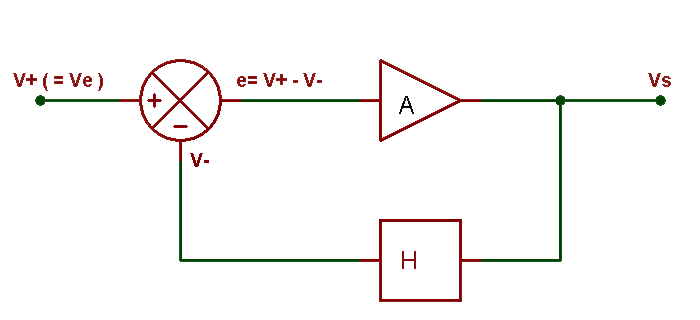
Bonjour,

Auriez-vous sous la main un exemple d'opérateur réalisable physiquement qui opère une rotation de Wick? Il s'agit de la transformation qui à associe , avec .
Une opération qui transforme un système oscillateur de réponse en un système de réponse .

Cordialement.
-----

[stefjm]

Je crois que j'ai trouvé une possibilité que je vous soumets.

Système de départ : oscillateur harmonique classique
Équation différentielle :
Racines de l'équation caractéristique :
Discriminant :
Réponse à l'échelon en : allure , h: échelon de Heaviside

Opération 1 : Multiplication par -1 de la sortie de l'oscillateur

Opération 2 : Contre réaction en mettant l'oscillateur et le gain de -1 à la place de A et H=1, retour unitaire

source http://electronique.aop.free.fr/cour_5.html

Système obtenu : double intégrateur de gain négatif
Équation différentielle :
Racines de l'équation caractéristique : , racine double
Discriminant :
Réponse à l'échelon en : allure

Opération 3 : Contre réaction à nouveau en mettant le résultat de l'opération 2 à la place de A et H=1, retour unitaire
Système obtenu : cascade de deux système du premier ordre
Équation différentielle :
Racines de l'équation caractéristique : , racine double
Discriminant :
Réponse à l'échelon en : allure

Ces trois opérations ont permis de passer d'un système ayant ses racines en imaginaires pures à un système ayant ses racine en réelles pures (rotation de Wick dans le plan complexe). Pour ce faire, on est passé par des racines nulles en translatant les racines le long de l'axe imaginaire (opération 2), puis le long de l'axe réel (opération 3).

On est passé d'un système qui répond en cosinus circulaire à un système qui répond en cosinus hyperbolique en remplaçant par .


Qu'en pensez-vous?

J'invite les septiques à venir constater le fonctionnement de ce système en vraie grandeur physique...

Cordialement.

[invite69d38f86]

la transformation de wick sert souvent à passer de la métrique euclidienne à celle de Minkowski .ça y ressemble beaucoup

[invite69d38f86]

ce n'est pas une réponse directe a ta question mais regarde ces montages
ils permettent de passer d'etats purs a des mélanges.
d'amplitudes de probabilités a des probabilites un peu comme au passage de mq a phys statistique.

[A voir en vidéo sur Futura]

[stefjm]

la transformation de wick sert souvent à passer de la métrique euclidienne à celle de Minkowski .ça y ressemble beaucoup

Mes opérations changent un système limite stable répondant en sinus (oscillateur) en un système instable répondant en sh (explosion) en passant par un système instable répondant en rampe (inertie).
On peut aussi peut-être les voir comme un changement de point de vu d'un même système?

ce n'est pas une réponse directe a ta question mais regarde ces montages
ils permettent de passer d'etats purs a des mélanges.
d'amplitudes de probabilités a des probabilites un peu comme au passage de mq a phys statistique.

Pour cette partie, c'est beaucoup plus loin de ce dont j'ai l'habitude.
Il y a probabilité quand c'est imaginaire pur et émergence d'une valeur moyenne quand c'est réel?
Avec la même rotation de pi/2 dans le plan complexe?

[stefjm]

Ces trois opérations ont permis de passer d'un système ayant ses racines en imaginaires pures à un système ayant ses racine en réelles pures (rotation de Wick dans le plan complexe). Pour ce faire, on est passé par des racines nulles en translatant les racines le long de l'axe imaginaire (opération 2), puis le long de l'axe réel (opération 3).

On est passé d'un système qui répond en cosinus circulaire à un système qui répond en cosinus hyperbolique en remplaçant par .

A noter que si on recommence les trois opérations, on repasse d'une réponse en cosh à une réponse en cos.

Si on note S le premier système, S' le second et H l'opérateur boucle fermée, cela revient à changer de base


Un avis sur cette représentation?
Est-ce de la vulgarisation de la boucle fermée et rotation de Wick de suffisamment bon niveau?

[invite69d38f86]

le H c'est la premiere lettre de quoi (harmonique; Hadamard?)

[invite69d38f86]

plutot Heaviside il me semble.

[invite69d38f86]

A noter que si on recommence les trois opérations, on repasse d'une réponse en cosh à une réponse en cos.

Si on note S le premier système, S' le second et H l'opérateur boucle fermée, cela revient à changer de base


Un avis sur cette représentation?
Est-ce de la vulgarisation de la boucle fermée et rotation de Wick de suffisamment bon niveau?

dis moi si j'ai bien compris;
H S et H^-1 sont des montages electroniques en série. H c'est ton rotateur de wick. S un montage quelconque. H^-1 a l'effet inverse de celuii de H
Est ce le meme que H mais ou la sortie est en entrée?
Et S' c'est le montage obtenu.
dans H on a les 3 étapes dont tu parlais au début.
mathémariquement ca ressemble a des compositions d'opérateurs. ce qui manque c'est la définition des fonctions sur lequel ils opérent.
s'agit il de fonctions réelles comme cos (f t) ou de fonctions complexes comme a cos (f t) + i b sin (f t) ou de fonctions vectorielles?

pour quelqu un comme moi qui n'a plus que de tres vagues souvenir sur ce qu'est un circuit oscillant, il serait bien d'avoir un schema du montage de H mais pas symbolique avec l'indication des composants electriques.

La ca deviendrait de la bonne vulgarisation.
dis toi bien que quand tu parles d'échelon , de gain etc je ne sais meme pas de quoi il s'agit
il faudrait un gros travail a ce niveau.
sinon l'idée d'un montage faisant une rotation de wick ca c'est tres intéressant.

[stefjm]

H S et H^-1 sont des montages electroniques en série. H c'est ton rotateur de wick. S un montage quelconque. H^-1 a l'effet inverse de celui de H

Oui.
H : opérateur de boucle fermée qui au système quelconque G associe G/(1+G)
H^-1 : opérateur de boucle qu'on ouvre qui au système G associe -G/(1-G)

Est ce le meme que H mais ou la sortie est en entrée?

H et H^-1 sont des systèmes systèmes différents.

Et S' c'est le montage obtenu.
dans H on a les 3 étapes dont tu parlais au début.

Oui

mathémariquement ca ressemble a des compositions d'opérateurs. ce qui manque c'est la définition des fonctions sur lequel ils opérent.
s'agit il de fonctions réelles comme cos (f t) ou de fonctions complexes comme a cos (f t) + i b sin (f t) ou de fonctions vectorielles?

Ces opérateurs opèrent sur des fonctions de transfert (transformée de Laplace ou Fourier Sortie/Entrée) ou sur les équations différentielles liant (sortie(t),entrée(t)).

pour quelqu un comme moi qui n'a plus que de tres vagues souvenir sur ce qu'est un circuit oscillant, il serait bien d'avoir un schema du montage de H mais pas symbolique avec l'indication des composants electriques.

La structure de la boucle fermée est celle que j'ai donnée au dessus.
G associe Entrée à Sortie du système
l'opérateur H transforme G en G/(1+G) en calculant la différence entre la nouvelle entrée et la sortie du nouveau système et la place sur l'entrée de G.
http://cyrille.pinton.free.fr/electr...rs/asserv2.gif

La ca deviendrait de la bonne vulgarisation.
dis toi bien que quand tu parles d'échelon , de gain etc je ne sais meme pas de quoi il s'agit
il faudrait un gros travail a ce niveau.
sinon l'idée d'un montage faisant une rotation de wick ca c'est tres intéressant.

Sûr que le vocabulaire est une plaie : personne n'appelle les choses pareils.
Gain : multiplication par k
Echelon : primitive du dirac, nulle pour t négatif et valant 1 pour t positif.

Cordialement.

[ornithology]

salut stefjm,
je fais un petit up sur ta question
qui apparait sous mon fil "théoreme de wick".
je pense avoir donné un montage dans "information which path"
tu en avais trouvé un autre?

[stefjm]

Bonjour,
Merci pour l'intérêt porté à ce fil.
Le post #2 de ce fil donne un opérateur physiquement réalisable qui transforme
- un oscillateur classique à deux pôles imaginaires, réponse impulsionnelle en sinus circulaire,
en
- un système à deux pôles réels oposés, réponse impulsionnelle en sinus hyperbolique.

Cordialement.

[ornithology]

Mon montage est optique avec deux écrans de Young.
sur le 1er on a des interférences dues a des oscillations.
cet écran on y fait également 2 fentes comme les 1eres avec un 2eme écran derriere.
un dispositif (polariseurs orthogonaux par exemple) supprime les interférences sur le 2eme écran.