Relativité de la simultanéité

[Merlin95]

ce qui se passe après le demi-tour est mieux compris en analysant la durée du voyage du retour. Il est à nouveau de 1 an pour J2 et à la fin, le jumeau J1 a 2 ans. Juste avant le voyage de retour,J1 était donc à nouveau à 1 année lumière et avait juste 2 ans - 1/10 année soit 1,9 ans. C'est normal car la phase d'accélération est identique à la phase de décélération. J1 prend donc pendant son demi-tour apparent (vu de J2) 2 fois 0,9 ans et effectue un aller retour "accéléré" partant de 1 année lumière, allant jusqu'à 10 a.l. , et revenant à 1 année lumière, avant le voyage de retour qui dure à nouveau 1 an.

Ce demi-tour de J1 par rapport à J2 n'a donc absolument pas les mêmes caractéristiques que celui de J2 par rapport à J1 , qui se faisait à âge et distance pratiquement constante. Ceci est bien sur du au champ de gravitation apparente extrêmement fort qui existe pour J2 et pas pour J1.

Donc au final quel âge a J1 et J2 quand ils se retrouvent ? 1,9 + 1 = 2,9 années pour J1 et 2 pour J2, c'est bien cela ?
-----

[phys4]

Donc au final quel âge a J1 et J2 quand ils se retrouvent ? 1,9 + 1 = 2,9 années pour J1 et 2 pour J2, c'est bien cela ?

Les durées totales avec les données initiales prises sont
pour J1 20 ans, les 2 fois 10 ans du voyage.
pour J2, 2 ans, puisque gamma = 10 et il fait deux trajets d'un an.

J1 voit les 2 ans, sous la forme 1 an ralentit 19,95 fois plus 1 an accéléré autant donc pendant 20 ans pour lui.
J2 voit 1/20 année de J1 pendant son trajet aller et 19,95 ans de J1 pendant son trajet retour.
Il n'y a rien d'autre à voir.

[Merlin95]

C'est dommage de voir qu'une personne prenne le temps de détailler les points de repère A, B, C et qu'une autre personne dise qu'il n'y a rien d'autre à voir que des éléments qui ne reprennent pas ce qui avait été détaillé auparavant.
Je vais essayer de reprendre le message de Archi3 en prenant en compte ces résultats finaux.

[Merlin95]

Le sédentaire va voir son jumeau au ralenti (car il s'éloigne, effet Doppler) pendant presque 20 ans, l'image qu'il recevra de son jumeau sera celle de ses 1 ans de voyage à la fin de cette phase, puis il verra son jumeau s'arrêter, prenant un rythme "normal", puis enfin, il le verra très accéléré (car il s'approche, effet Doppler), en quelques mois le sédentaire verra son jumeau prendre un an de plus.

Le il c'est le voyageur. Car si c'est le sédentaire, vous dîtes qu'il a vu le voyageur passé 1 an, et au retour aussi 1 an donc si c'est ca, il le verrait pas en accéléré.

[Merlin95]

ce qui se passe après le demi-tour est mieux compris en analysant la durée du voyage du retour. Il est à nouveau de 1 an pour J2 et à la fin, le jumeau J1 a 2 ans

20 ans j'imagine.

[phys4]

20 ans j'imagine.

Bien sur, je pensais que les points de repère n'étais pas importants : il y a simplement un aller que vous pouvez noter AB et un retour à noter DE.

Archi a beaucoup compliqué les choses et fait un joli mélange.

[Merlin95]

On peut résumer, 1 an pour l'aller, un an pour le retour, 2 ans au total pour l'un, et pour l'autre 10 ans, et 10 ans donc 20 ans, mais quand on dit cela, on a en fait pas dit grand chose.

Du coup comment ca se passe ?

Le fait d'imaginer que le retour est fait instantanément cache certaines choses qu'il me semble utile de préciser.
Ce qui se passe dans les périodes de décélération et d'accélération me semble peut-être à tord décisif.

En effet, imaginons qu'il n'y ait pas de décélération, on pourrait alors dire qu'entr A et C (le moment où le voyageur passe au dessus de la planète visitée), le temps propre du voyageur est de 1 an, et ce temps correspond à un temps de 10 ans pour le sédentaire.
La distance propre entre A et B est de 10 a.l., et la distance pour le voyageur est de 1 a.l.
Le sédentaire voit l'horloge du voyageur battre plus lentement que la sienne.
Mais peut-on dire que le voyageur voit aussi l'horloge du sédentaire au ralenti ?
Si oui, si le sédentaire est plus vieux lorsqu'ils se retrouvent, alors à quel moment vieillit-il plus vite (son horloge bat plus rapidement vu du voyageur) ?

[phys4]

On peut résumer, 1 an pour l'aller, un an pour le retour, 2 ans au total pour l'un, et pour l'autre 10 ans, et 10 ans donc 20 ans, mais quand on dit cela, on a en fait pas dit grand chose.

Du coup comment ca se passe ?

Le fait d'imaginer que le retour est fait instantanément cache certaines choses qu'il me semble utile de préciser.
Ce qui se passe dans les périodes de décélération et d'accélération me semble peut-être à tord décisif.

En effet, imaginons qu'il n'y ait pas de décélération, on pourrait alors dire qu'entre A et C (le moment où le voyageur passe au dessus de la planète visitée), le temps propre du voyageur est de 1 an, et ce temps correspond à un temps de 10 ans pour le sédentaire.
La distance propre entre A et B est de 10 a.l., et la distance pour le voyageur est de 1 a.l.
Le sédentaire voit l'horloge du voyageur battre plus lentement que la sienne.
Mais peut-on dire que le voyageur voit aussi l'horloge du sédentaire au ralenti ?

Il faut faire la part entre la mesure dans un laboratoire et ce que l'on peut observer pour un vaisseau spatial.
Dans certains problèmes, il est parfois difficile de reconnaitre dans quel sens il faut appliquer le facteur de Lorentz, un façon simple de se'y retrouver et de se souvenir que pour faire la mesure il faut un référentiel avec deux horloges distantes synchronisées qui observe une horloge mobile, donc dans un autre référentiel.
C'est toujours l'horloge unique qui semble aller plus lentement que les deux autres. Vous remarquerez que les deux horloges synchronisées implique que ce référentiel rest inertiel pendant toute la mesure, ce qui rejoint l'une des explications données : le vaisseau mobile ne peut pas avoir deux horloges synchronisées dans son référentiel, c'est l'effet de l'accélération.

Revenons à la question posée : nous avons le droit de négliger l'accélération, mais pas ses conséquences pour le (les) référentiels du vaisseau.
Ce qui observable c'est seulement les signaux échangés, ils sont affectés d'un facteur de distorsion de 19,95 soit dans un sens, soit l'autre symétriquement.
Ce qui n'est pas symétrique, ce sont les durées de mesure : le vaisseau reçoit les signaux de la Terre pendant 1 an dans un sens et 1 an dans l'autre, faites le total, il voit 20 ans de J1 en deux ans seulement.
J1 verra les 2 ans de J2 en 20 ans, car il mettra 19,95 ans pour recevoir la totalité du rapport d'aller avant celui de retour.

Vous voyez apparaitre une raison complémentaire de dissymétrie : c'est J2 qui maitrise les durées, car il se déplace par rapport aux signaux. Alors que J1 passif, ne peut que recevoir ce qu'on lui envoie.

[Merlin95]

Ca aurait été bien que tu dises à quoi correspond 19,95, là comme ca, excuse moi, je pourrais pas dire à quel rapport ça correspond.

[Merlin95]

Ce lien est assez détaillé :

http://hachel.chez-alice.fr/rela3.htm

Avec ce point que je trouve crucial :

Les deux jumeaux se voient réciproquement vieillir moins vite à l'aller, et selon la même équation: et réciproquement vieillir plus vite au retour:

C'est là un des noeuds du problème et ce sur quoi je voulais justement des éclaircissements.

[Merlin95]

Et on a bien la symétrie dont parle la RR.

[Amanuensis]

Avec ce point que je trouve crucial :

Les deux jumeaux se voient réciproquement vieillir moins vite à l'aller, et selon la même équation: et réciproquement vieillir plus vite au retour

C'est là un des noeuds du problème et ce sur quoi je voulais justement des éclaircissements.

L'affirmation est correcte, mais passe complètement à côté du point crucial.

Déjà, au mot «voir» au sens propre, c'est exactement la même chose en classique: c'est l'effet Doppler, et il est symétrique.

Du fait qu'en classique la phénoménologie est la même, ce ne peut pas être explicatif pour la RR.

Ensuite, ce dont parle l'affirmation est le taux de vieillissement, «moins vite», «plus vite». Or ce qui nous intéresse c'est le vieillissement total, pas le taux.

Seulement, en classique, on ne fait pas la différence, parce que le vieillissement total est le taux fois la durée du voyage, et le «réflexe» est de prendre une durée égale pour les deux.

Mais cela ne marche pas en RR. Le vieillissement de l'autre tel que vu est le taux vu intégré sur le temps.

Et les durées propres des deux phases ne sont pas les mêmes pour les deux. L'intégration donne donc des vieillissements vus différents. L'asymétrie est dans les durées propres.

Remarquons que présenté comme ça, cela paraît tautologique: parce que les durées propres sont différentes, la symétrie apparente des taux de vieillissement donne une intégrale différente. Oui, mais ce n'est pas tautologique, juste cohérent. Et ce aussi bien en classique qu'en RR. Et le calcul avec les équations de la RR montre cette cohérence.

Le seul point, une fois de plus, est de ne pas penser en termes de durées absolues. Le «paradoxe» des jumeaux ne prouve pas que les durées propres des voyages sont différentes, il se contente de l'illustrer.

Si on cherche l'origine de la dissymétrie, ce n'est pas réfléchir à la symétrie du Doppler qui va aider.

Pour moi (mais il y a d'autres manières de voir), l'image est celle d'un triangle, celui formé en 4D par les trois événements, séparation (A), demi-tour (B) et réunion (C). La dissymétrie est alors évidente: en géométrie euclidienne la différence de longueur entre AC et la somme des longueurs de AB et BC dépend de l'angle en C. La transcription en géométrie minkowskienne est: la différence entre la durée de AC et la somme des durées AB et BC dépend du changement de vitesse en C. La symétrie d'une phase est simplement la symétrie d'un angle: les deux droites porteuses de AC et AB sont symétriques l'une de l'autre, de même que les droites porteuses de CA et CB. Mais cela n'entraîne pas l'égalité de longueur des deux chemins!

Une telle vision (i.e., «lire les diagrammes de Minkowski») n'est peut-être pas facile à acquérir, mais elle oblige à (ou permet de...) ne pas penser en temps absolu. Sur ces diagrammes, les durées (propres, les seules physiques) ne se lisent pas sur l'axe de coordonnées mais comme des longueurs de segments (ou de courbes). Application: dans le cas des jumeaux elle permet de voir immédiatement à la fois la symétrie par phase (celle générale entre deux droites) et la non-symétrie (dans un triangle non plat il n'y a pas, de manière évidente, de symétrie entre un côté et l'ensemble des deux autres).

Note: je n'ai pas pris l'interprétation de «voir» pour les taux de vieillissement comme la «dilatation du temps», qui est la différence dans les formules entre doppler classique et doppler relativiste, autrement dit le doppler relativiste corrigé du doppler classique. Car cette correction n'est pas le phénomène tel que constaté, mais le résultat d'un calcul qui implique les formules de la RR.

[Amanuensis]

Corrigendum:

[L'édition de message post envoi est devenu un cauchemar pour moi (pb du forum, ou de mon navigateur, ou de la combinaison des deux, je ne sais), et je n'ai pas encore réussi à m'adapter.]

Le texte est mieux dit comme suit pour un passage:

------------

Seulement, en classique, on ne fait pas la différence, parce que le vieillissement total est la somme des taux fois la durée de la phase (phase aller et phase retour), et le «réflexe» est de prendre les durées des phases égales tant pour les deux observateurs que pour les deux phases.

Mais cela ne marche pas en RR. Le vieillissement de l'autre tel que vu est le taux vu intégré sur la durée propre de l'observateur, et les durées (propres) des phases ne sont pas les mêmes pour les observateurs. Phases de durées égales pour l'un, mais différentes pour l'autre.L'intégration donne donc des vieillissements vus différents.

L'asymétrie est dans les durées propres.

[Paradigm]

Bonjour à tous,

Une formalisation des jumeaux de Langevin dans le cadre la RR basée sur l'image du triangle (en 4D) évoquée par Amanuensis

Cordialement,

[Amanuensis]

J'ai pris le temps (long) de faire une figure.



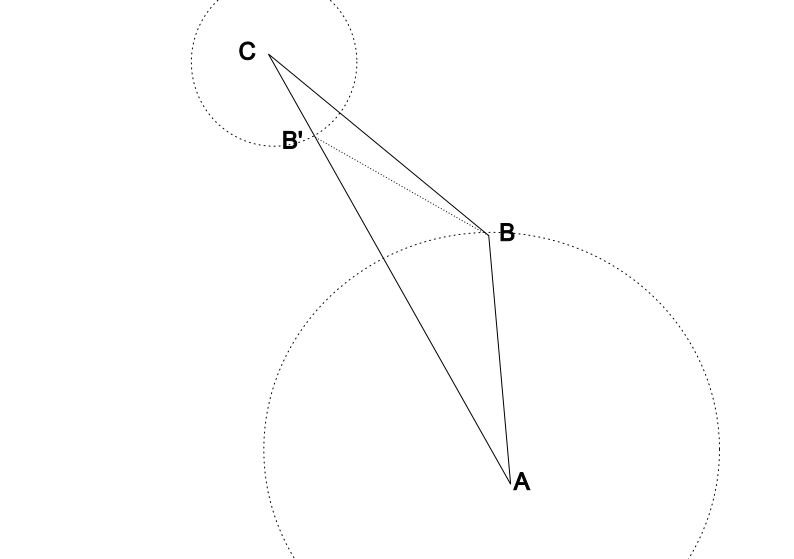
Le temps est vers le haut. A est l'événement de séparation, B l'événement demi-tour, C l'événement réunion et B' l'événement «vue par l'inertiel du demi-tour».

La ligne BB' est donc le trajet de la lumière véhiculant l'image du demi-tour. L'angle en B est la modification de vitesse lors du demi-tour.

Les deux cercles indiquent les régions de symétrie. La partie intermédiaire, hors des cercles, est la partie non symétrique, à l'origine du différentiel de vieillissement.

Dans un tel diagramme les longueurs de segment ne représentent pas exactement les durées (ou distances) propres (si c'était le cas, BB' serait de longueur nulle) ; ce n'est donc pas correct quantitativement (ce ne serait pas possible, on peut peut pas faire une carte euclidienne «isométrique» de la géométrie de Minkowski. Pour le quantitatif, faut faire les calculs.

[Amanuensis]

PS: Ne pas chercher la signification des coordonnées, des axes. Il n'y en a pas, le dessin est volontairement sans coordonnées significatives, comme on peut le faire en géométrie. La seule contrainte est que les lignes de genre temps (comme AB, AC et BC) soit plus proches de la verticale que les lignes de genre lumière (comme BB').

On peut ensuite raisonner et calculer sur ces diagrammes comme on le fait en géométrie sans coordonnées, avec «juste» une modification sur les normes et projections. J'avais donné ces calculs pour le «triangle de Langevin» dans une discussion ancienne, que j'ai la flemme de retrouver.

[Archi3]

Hello
désolé pour le temps de latence, j'ai été éloigné de mon ordi pour des causes indépendantes de ma volonté (mais dépendantes de ma distraction ..)
tout d'abord pour références, je corrige les coquilles de mon premier post. L'idée du post venait de montrer en quoi le voyage vu par J1 ou par J2 était totalement différent (et incidemment, montrer l'impossibilité de raisonner dans un référentiel "attaché" au jumeau voyageur).
L'idée est que chaque jumeau peut à bon droit se demander entre les deux rencontres initiales et finales, un truc du genre "tiens je me demande où mon jumeau est en ce moment et quel âge (propre) il peut avoir, même si je sais bien que ce n'est pas forcément le mien car j'ai bien compris la Relativité).

Pour le jumeau J1 galiléen, cette question est raisonnablement posée et la réponse est assez simple. Le référentiel galiléen (R1) attaché à J1 permet une synchronisation de toutes les horloges fixes dans ce référentiel et il est raisonnable d'attacher à chaque évènement de J2 :
* une position coincidente dans R1
* un temps t coïncident mesuré dans R1
* un temps propre tau1 mesuré par J1 à cet instant t (ce sera le même)
* un temps propre tau2 mesuré par J2 au même instant (tau2≠ t)

On obtient pour les 5 évènements décrits plus haut (x1 sera toujours égal à zéro).
A : x2 = 0 , t =tau1= 0 , tau2 = 0
B,: x2 = 10 a.l, t=tau1= 10 ans , tau2 = 1 an
C , D : comme B à peu de choses près (la durée du demi-tour supposé très brève)
E : x2 = 0 , t=tau1 = 20 ans , tau2 = 2 ans

Pour J2 c'est là que ça se complique. J2 n'étant pas inertiel, dans quel(s) référentiel(s) mesurer la position et l'âge de J1, et en particulier quel instant de J1 doit être considéré comme simultané avec J2 pour qu'il puisse se demander "tiens quel âge a mon jumeau en ce moment ?" une question que la plupart des lecteurs trouvera sans doute assez anodine , quand on connait les TL (la question inverse posée par J1 EST assez anodine).
La seule façon raisonnable d'attacher un référentiel qui permette de répondre à cette question est de considérer le référentiel tangent à J2, c'est à dire le référentiel galiléen dans lequel il parait immobile à l'instant t. Le problème est ça donne les résultats absurdes que j'ai décrit.

Dans le référentiel tangent à J2, on obtient pour les 5 évènements décrits plus haut (c'est x2 qui sera toujours zéro) :
A : x1=x2 = 0 , t =tau1= 0 , tau2 = 0
B,: x1 = - 1 a.l, tau1= 0,1 ans , t=tau2 = 1 an

C : x1 = -10 a.l., tau1 = 10 an, t=tau2 = 1 an(+ epsilon)

D : x1 = - 1 a.l, tau1= 19,9 ans , t=tau2 = 1 an (+ 2 epsilon)


E : x1 = 0 , tau1 = 20 ans , tau2 = 2 ans

Les variations subies par J1 paraissent absurdes (déplacements superluminiques, vieillissement soudain très accéléré...): mais en fait le problème fondamental est que "l'ensemble des référentiels tangents" n'est PAS un référentiel. Il ne constitue pas une cartographie (x,t) de l'espace temps. Il donne lieu à des phénomènes aberrants, et même encore plus que ce qui a été décrit : par exemple le jumeau J1 peut remonter le temps (si le jumeau J2, après avoir fait une pause sur une planète, repart dans le même sens à gamma=10 au lieu de revenir en arrière, J1 redeviendra "jeune" !). Ou un moment de J1 peut être simultanés avec plusieurs moments de J2. Mais le problème fondamental est qu'il n'y a pas de référentiel rigide attaché à J2 (les coordonnées de Rindler ne pavent pas tout l'espace temps et en plus elles ne valent que pour une accélération constante, ce qui n'est pas le cas de J2). Bref il n'y a aucune manière naturelle de décider "quel" moment de J1 est simultané pour J2 dans "son" réferentiel :et donc il n'y a absolument aucune symétrie entre les 2 (en quelque sorte le "voyage" de J1 par rapport à J2 ne peut pas etre correctement décrit). Ce genre de problème existe DEJA dans un espace plat pour un observateur accéléré - on comprend qu'il puisse se poser de manière encore plus intrinsèque et inévitable pour un champ de gravitation réel comme un trou noir....

[Merlin95]

Hello
désolé pour le temps de latence, j'ai été éloigné de mon ordi pour des causes indépendantes de ma volonté (mais dépendantes de ma distraction ..)
tout d'abord pour références, je corrige les coquilles de mon premier post. L'idée du post venait de montrer en quoi le voyage vu par J1 ou par J2 était totalement différent (et incidemment, montrer l'impossibilité de raisonner dans un référentiel "attaché" au jumeau voyageur).
L'idée est que chaque jumeau peut à bon droit se demander entre les deux rencontres initiales et finales, un truc du genre "tiens je me demande où mon jumeau est en ce moment et quel âge (propre) il peut avoir, même si je sais bien que ce n'est pas forcément le mien car j'ai bien compris la Relativité).

Pour le jumeau J1 galiléen, cette question est raisonnablement posée et la réponse est assez simple. Le référentiel galiléen (R1) attaché à J1 permet une synchronisation de toutes les horloges fixes dans ce référentiel et il est raisonnable d'attacher à chaque évènement de J2 :
* une position coincidente dans R1
* un temps t coïncident mesuré dans R1
* un temps propre tau1 mesuré par J1 à cet instant t (ce sera le même)
* un temps propre tau2 mesuré par J2 au même instant (tau2≠ t)

On obtient pour les 5 évènements décrits plus haut (x1 sera toujours égal à zéro).
A : x2 = 0 , t =tau1= 0 , tau2 = 0
B,: x2 = 10 a.l, t=tau1= 10 ans , tau2 = 1 an
C , D : comme B à peu de choses près (la durée du demi-tour supposé très brève)
E : x2 = 0 , t=tau1 = 20 ans , tau2 = 2 ans

Pour J2 c'est là que ça se complique. J2 n'étant pas inertiel, dans quel(s) référentiel(s) mesurer la position et l'âge de J1, et en particulier quel instant de J1 doit être considéré comme simultané avec J2 pour qu'il puisse se demander "tiens quel âge a mon jumeau en ce moment ?" une question que la plupart des lecteurs trouvera sans doute assez anodine , quand on connait les TL (la question inverse posée par J1 EST assez anodine).
La seule façon raisonnable d'attacher un référentiel qui permette de répondre à cette question est de considérer le référentiel tangent à J2, c'est à dire le référentiel galiléen dans lequel il parait immobile à l'instant t. Le problème est ça donne les résultats absurdes que j'ai décrit.

Dans le référentiel tangent à J2, on obtient pour les 5 évènements décrits plus haut (c'est x2 qui sera toujours zéro) :
A : x1=x2 = 0 , t =tau1= 0 , tau2 = 0
B,: x1 = - 1 a.l, tau1= 0,1 ans , t=tau2 = 1 an

C : x1 = -10 a.l., tau1 = 10 an, t=tau2 = 1 an(+ epsilon)

D : x1 = - 1 a.l, tau1= 19,9 ans , t=tau2 = 1 an (+ 2 epsilon)


E : x1 = 0 , tau1 = 20 ans , tau2 = 2 ans

Ok merci, c'est plus clair maintenant. Merci à Amanuensis aussi pour le diagramme.

[mach3]

PS: Ne pas chercher la signification des coordonnées, des axes. Il n'y en a pas, le dessin est volontairement sans coordonnées significatives, comme on peut le faire en géométrie. La seule contrainte est que les lignes de genre temps (comme AB, AC et BC) soit plus proches de la verticale que les lignes de genre lumière (comme BB').
.

C'est le genre d'approche qu'on devrait voir plus souvent.

m@ch3

[Amanuensis]

Merci à Amanuensis aussi pour le diagramme.

En espérant que cela ne soit pas mal pris, je ne suis pas trop intéressé par les merci (mais d'autres oui...). Par contre, je serais intéressé à savoir si cela a amené quelque chose aidant la compréhension, et quoi exactement, pour savoir si c'est réutilisable pour d'autres discussions, comment le modifier éventuellement, etc. En particulier, j'ai cherché à illustrer que la symétrie dans la vue l'un de l'autre est correcte dans les phases initiales et finales, mais pas dans la phase intermédiaire. Est-ce que cela aide (un peu, beaucoup, pas du tout, ...) à voir comment sont compatibles la symétrie mentionnée dans le message de 1h39 et la dissymétrie des vieillissements?

[Merlin95]

J'ai ma vitesse d'assimilation qui est très lente. Cela ne m'a pas aidé pour l'instant, ca dépasse mes capacités actuelles de compréhension sur le sujet, mais je continue à essayer de comprendre.

[Merlin95]

Mes retours viendront un peu plus tard si je me suis capable d'en faire un retour compréhensible et exploitable.

[Merlin95]

Le temps est vers le haut.

On peut avancer que l'espace est vers la droite ?

A est l'événement de séparation, B l'événement demi-tour, C l'événement réunion et B' l'événement «vue par l'inertiel du demi-tour».

je comprends.

La ligne BB' est donc le trajet de la lumière véhiculant l'image du demi-tour. L'angle en B est la modification de vitesse lors du demi-tour.

je comprends.

Les deux cercles indiquent les régions de symétrie. La partie intermédiaire, hors des cercles, est la partie non symétrique, à l'origine du différentiel de vieillissement.

Je ne comprends pas ce point, en particulier pourquoi on parle ici de symétrie.

Dans un tel diagramme les longueurs de segment ne représentent pas exactement les durées (ou distances) propres (si c'était le cas, BB' serait de longueur nulle) ; ce n'est donc pas correct quantitativement (ce ne serait pas possible, on peut peut pas faire une carte euclidienne «isométrique» de la géométrie de Minkowski. Pour le quantitatif, faut faire les calculs.

J'ai rien à apporter à ce point, n'étant pas assez compétant pour avoir un avis.

En particulier, j'ai cherché à illustrer que la symétrie dans la vue l'un de l'autre est correcte dans les phases initiales et finales, mais pas dans la phase intermédiaire. Est-ce que cela aide (un peu, beaucoup, pas du tout, ...) à voir comment sont compatibles la symétrie mentionnée dans le message de 1h39 et la dissymétrie des vieillissements?

Non en ce qui me concerne mais peut-être est-ce lié aux points précédents sur les cercles.

[Amanuensis]

On peut avancer que l'espace est vers la droite ?

Ou vers la gauche... L'espace n'est pas orienté, contrairement au temps. Les directions spatiales c'est tout ce qui est plus près de l'horizontale que les lignes de genre lumière (représentées souvent à 45°, sans que ce soit une nécessité).

En RR ce qui est important c'est la distinction entre genre temps, le genre espace et surtout les directions de genre lumière.

Je ne comprends pas ce point, en particulier pourquoi on parle ici de symétrie.

Si on se limite à ce qu'il y a à l'intérieur d'un des cercles, les situations des deux jumeaux sont parfaitement symétriques (géométriquement, c'est la symétrie miroir par rapport à la bissectrice, l'orientation n'a pas d'importance, à l'instar d'un triangle isocèle dessiné dans une orientation quelconque). En particulier, ils se voient l'un l'autre vieillir moins vite (à l'aller, cercle du bas) ou plus vite (au retour, cercle du haut) qu'eux-mêmes, mais identiquement. Ce sont ces zones qui font croire que le phénomène est symétrique.

Mais si on regarde toute la figure, et non pas juste les deux zones encerclées, elle manifeste une asymétrie entre les deux voyage (AC via B' d'un côté, et ABC de l'autre). C'est la position de B et B' qui est différente pour les deux: B est au milieu du chemin ABC, alors que B' est plus près de C que de A sur le chemin AC direct. Dire que le taux de vieillissement est perçu symétriquement est vrai vers le début ou vers la fin (les zones encerclés) mais la position différente de B et B' (au milieu ou non) rompt la symétrie.

[Comme toute figure en géométrie classique, elle ne fait qu'illustrer, supporter l'intuition. La confirmation demande des calculs, qu'on fait en géométrie classique avec de la trigonométrie. Et on peut faire la même chose avec un tel diagramme, avec trigonométrie adaptés (la trigonométrie hyperbolique, avec des sinh et cosh à la place des sin et cos). Perso je trouve bien plus facile d'obtenir un support d'intuition ainsi plutôt qu'avec des calculs en coordonnées, que ce soit en géométrie classique ou sur un diagramme de Minkowski en RR.

Au fond, j'ai du mal à comprendre comment des calculs en coordonnées comme on en voit sur ce fil aident réellement. Ils ne font que confirmer, de manière «aveugle» ce que dit directement le paradoxe (l'augmentation d'âge est différentes) sans aider (pour moi) à avoir une intuition sur le fond permettant d'aborder d'autres cas. On connaît à l'avance le résultat des calculs, et donc ce devrait être la méthodologie suivi par le calcul qui aide à comprendre le résultat... Bref, je propose une autre voie (et voix), pour chercher ce qui peut aider.]

[mach3]

Petit commentaire sur le schéma en passant, au lieu des cercles, est-ce que ça ne devrait pas être des hyperboles (pas sûr que ça aide à la compréhension, question d'exactitude, c'est tout).

m@ch3

[Archi3]

J'ai pris le temps (long) de faire une figure.

Pièce jointe 366266

Le temps est vers le haut. A est l'événement de séparation, B l'événement demi-tour, C l'événement réunion et B' l'événement «vue par l'inertiel du demi-tour».

La ligne BB' est donc le trajet de la lumière véhiculant l'image du demi-tour. L'angle en B est la modification de vitesse lors du demi-tour.

Les deux cercles indiquent les régions de symétrie. La partie intermédiaire, hors des cercles, est la partie non symétrique, à l'origine du différentiel de vieillissement.

Dans un tel diagramme les longueurs de segment ne représentent pas exactement les durées (ou distances) propres (si c'était le cas, BB' serait de longueur nulle) ; ce n'est donc pas correct quantitativement (ce ne serait pas possible, on peut peut pas faire une carte euclidienne «isométrique» de la géométrie de Minkowski. Pour le quantitatif, faut faire les calculs.

j'ai une petite critique à faire sur ce diagramme : le caractère "isocèle" du triangle (donc la durée égale du voyage aller et du voyage retour) n'existe QUE dans le référentiel du jumeau galiléen (et donc lorsque sa "droite" est verticale). Dans d'autres référentiels galiléens , le triangle est (éventuellement très) dissymétrique. Par exemple dans le référentiel galiléen accompagnant le jumeau voyageur à l'aller (à gamma=10 constant), le voyage est vu très différemment : le jumeau voyageur commence par rester immobile pendant un an, tandis que J1 s'éloigne constamment à gamma=10 (il n'aura vieilli que de 0,1 ans). Puis au moment du "demi-tour" , le jumeau J2 part à la poursuite de J1 (qui continue à s'éloigner à un gamma de 10...) à un gamma d'environ 200, et le voyage dure environ 200 ans ....

[mach3]

A la racine, il y a la difficulté à représenter de la géométrie de Minkowski sur une feuille de papier (ou un écran) euclidienne. Cela vaut pour ma critique cercle/hyperbole et pour la critique sur le caractère isocèle. On ne peut pas tout avoir, il faut faire des choix.

On peut par exemple dessiner l'analogue euclidien de la situation (et je crois que c'est ce qui a été fait), et donc le triangle est toujours isocèle et les parties symétriques délimitées par des cercles.
Ou alors on dessine le cas Minkowskien, et le dessin depend du mapping Minkowski->Euclide que l'on choisit. Un triangle "isocèle Minkowskien" ne sera représenté comme un triangle isocèle euclidien que dans certains mappings.

m@ch3

[Merlin95]

Si on se limite à ce qu'il y a à l'intérieur d'un des cercles, les situations des deux jumeaux sont parfaitement symétriques (géométriquement, c'est la symétrie miroir par rapport à la bissectrice, l'orientation n'a pas d'importance, à l'instar d'un triangle isocèle dessiné dans une orientation quelconque).

La bissectrice de l'angle ABC, c'est bien cela ? Lorsque B parcourt le cercle centré en A, le triangle ABC n'est pourtant plus symétrique. Dans quel sens, où est la symétrie ?

[Amanuensis]

La bissectrice de l'angle ABC, c'est bien cela ? Lorsque B parcourt le cercle centré en A, le triangle ABC n'est pourtant plus symétrique. Dans quel sens, où est la symétrie ?

Si on note D l'intersection de AC avec le cercle du bas, la symétrie est entre AD et AC. AD est la partie du mouvement de l'inertiel qui va de la séparation (en A) à D, AC la partie du mouvement de l'autre entre la séparation et le demi-tour. Ces deux partie (AD et AC) sont des segments de droites donc des MRU, et sont symétriques l'un de l'autre, ADC formant un triangle isocèle.

Les cercles ne sont pas des parcours de quoi que ce soit, juste une manière symbolique de représenter l'égalité AD et AC.

[En fait je réalise que le problème est qu'il n'est pas facile d'interpréter, sans habitude, ce qui est «conservé» de la géométrie minkowskienne dans cette représentation euclidienne, nécessairement déformée, comme une carte plane de la surface terrestre la déforme... L'aspect isocèle en 4D n'est pas conservé pour tous les triangles dans la cartographie. Que ce soit la géométrie sphérique ou hyperbolique, la représentation sur un plan ne peut pas être «littérale».

Bon..., je pense que c'est un échec, c'est une technique qui ne marche qu'une fois les règles du jeu comprises. Pour moi, pour Mach3, mais c'est tout.]

[Archi3]

Si on note D l'intersection de AC avec le cercle du bas, la symétrie est entre AD et AC. AD est la partie du mouvement de l'inertiel qui va de la séparation (en A) à D, AC la partie du mouvement de l'autre entre la séparation et le demi-tour. Ces deux partie (AD et AC) sont des segments de droites donc des MRU, et sont symétriques l'un de l'autre, ADC formant un triangle isocèle.

peut etre que je n'ai pas compris, mais je ne vois pas à quel évènement D correspond (pour J1). Est ce le point où J1 a atteint 1 an, l'âge de J2 aura quand il fera son demi-tour ? d'un autre coté comme tu dis les représentations euclidiennes ne permettent pas d'lllustrer le temps propre simplement (en tout cas pas comme une "longueur", puisque le temps propre de n'importe quel segment de longueur "euclidienne" donnée tend vers zéro quand il se rapproche du cône de lumière).
Bref je ne suis pas certain de voir ce que le diagramme permet d'éclaircir pour quelqu'un qui a les idées un peu confuses sur l'effet de la métrique minkowskienne.... Comme suggère Mach3, représenter les hyperboles d'asymptotes le cone de lumière (qui est le lieu réellement suivi par l'extrémité des 4-vecteurs lors des "quasi-rotations" de la TL ) aide peut etre à mieux voir la déformation du triangle ... Mais bien sur la symétrie n'est plus aussi facilement visualisable, deux trajets de même temps propre n'ont plus la même longueur euclidienne).