Relativité de la simultanéité

[Deedee81]

Au contraire, la question est très bonne

Je n'ai pas dit qu'elle était mauvaise
-----

[Amanuensis]

Alors précisons: Non, cette question peut se poser AUSSI dans un forum scientifique (celui-ci en particulier), et dans le cadre de la physique,et non seulement «dans les interrogations plutôt philo-physique».

Et NON, ce n'est pas une bonne comparaison que de la faire avec une question «Qu'est-ce que le temps?». La différence est qu'une horloge est un objet tangible, un instrument de mesure, qui a des caractéristiques comme limites de fonctionnement, précision, répétabilité, etc.

[mach3]

C'est-à-dire commencer par le commencement : qu'est-ce qu'une horloge

quelques éléments de réponse ici pour les lecteurs intéressés : http://forums.futura-sciences.com/ep...ml#post6144894

m@ch3

[Nicophil]

"En attendant, la science contemporaine n'a pas tranché un débat qui reste philosophique" : https://www.jstor.org/stable/4303428...n_tab_contents

[Zefram Cochrane]

Bonjour,


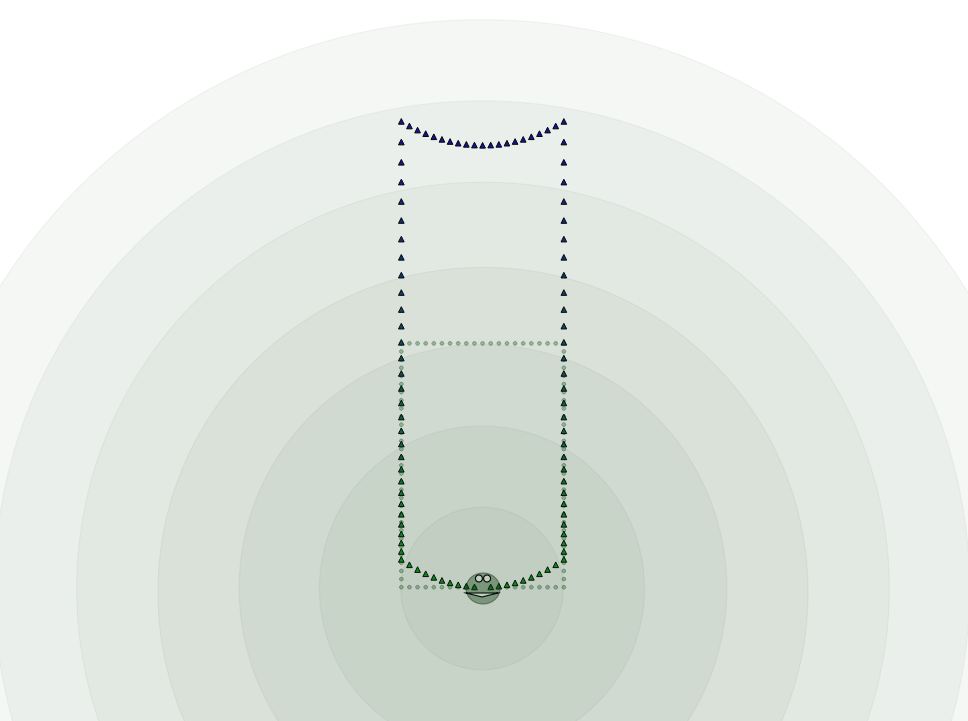
Voici le schéma d'un observateur situé dans un ascenseur rectangulaire (points vert) quand il est plongé dans un référentiel inertiel; chaque point est séparé d'un point adjacent d'une longueur propre de 1 000 000s.l .

A T=0s, l'observateur accélère avec une accélération propre de 10m/s² et les points d'une accélération propre égale à c/(30Ms.l+Z) Z étant la coordonnée verticale d'un point à T=0s par rapport à l'observateur.

Au fur et à mesure que la vitesse par rapport au référentiel initial augmente, l'observateur constate ( par ce qu'il a une vision euclidienne de son environnement) que la cage d'ascenseur semble se déformer jusqu'à un certain point ( plus la distance initale séparant l'observateur d'un point est importante et plus le point semble dévier de sa position initiale comme indiquée sur le schéma du fait de l'aberration de la lumière).

A partir d'un certain temps, l'ascenseur prend sa forme définitive dans le champ de pesanteur ainsi simulé comme indiqué sur le schéma (triangles).

Si initialement, la coordonnée X et Z de chaque point y est mentionnée dessus (graduation), le fait que l'observateur déformé ne modifie en rien les coordonnées indiquée dessus.

par contre la coordonnnée X' et Z' apparente de ces points n'est plus la même.

d'où mes question :
1) comme formuler ce que je viens de dire en utilisant une sémantique correcte?
2) la cage d'ascenseur ici simulée est sensé représenter une structure infiniment rigide; je ne comprends pas pourquoi je ne peut utiliser ce genre de structure dans le cadre d'un exercice de RG et encore moins dans le cadre d'un exercice de RR?

[Amanuensis]

2) la cage d'ascenseur ici simulée est sensé représenter une structure infiniment rigide; je ne comprends pas pourquoi je ne peut utiliser ce genre de structure dans le cadre d'un exercice de RG et encore moins dans le cadre d'un exercice de RR?

L'infinie rigidité implique une vitesse infinie de la causalité entre deux points distants de l'objet.

Réciproquement donc, une vitesse finie de la causalité implique une valeur minimale à l'élasticité pour une accélération donnée a pour que l'objet reprenne ensuite ses dimensions. [En très grossier, si d est la distance maximale entre un point de l'objet et le point d'application de la force (on suppose un point unique d'application de la force), il faut une durée d/c pour que l'accélération se propage dans l'objet, le point d'application s'est alors déplacé de 1/2 a d²/c², et donc l'élasticité doit âtre suffisante pour accepter une dilatation de 1/2 ad/c². C'est le plus souvent très faible, mais non nul].

Si l'élasticité est trop faible, l'objet se déforme plastiquement ou casse. En aucun cas il ne garde sa longueur (ce qui serait impliqué par une rigidité infinie.)

Voir le «paradoxe» de la clé et la serrure.

[muzoter]

###############
- avais initié un topic il fut un temps :

http://forums.futura-sciences.com/ep...e-horloge.html

or la conclusion ayant semblé devoir être que les jumeaux dits de langevin quand ils se revoient, ayant au préalable activé deux horloges de même facture au même instant t0, ont sur leurs cadrans respectifs exactement la même heure arrête tout d'suite ça va fermer m'étais-je dis à l'époque

[phys4]

or la conclusion ayant semblé devoir être que les jumeaux dits de langevin quand ils se revoient, ayant au préalable activé deux horloges de même facture au même instant t0, ont sur leurs cadrans respectifs exactement la même heure arrête tout d'suite ça va fermer m'étais-je dis à l'époque

Certaines personnes ont des difficultés à oublier le temps absolu, pourquoi voulez vous que des horloges identiques, mais séparées, ne vivent pas leurs vies indépendantes?
Cela ne me choque que l'on ne comprenne pas, ce qui est remarquable, c'est plutôt le nombre de personnes qui arrivent à assimiler les bases.

Mais il faudrait commencer par des exercices simples sur les équations de Lorentz.

[Amanuensis]

or la conclusion ayant semblé devoir être que les jumeaux dits de langevin quand ils se revoient, ayant au préalable activé deux horloges de même facture au même instant t0, ont sur leurs cadrans respectifs exactement la même heure

Ce n'était pas le cas du tout, vous racontez n'importe quoi.

[LLphy]

or la conclusion ayant semblé devoir être que les jumeaux dits de langevin quand ils se revoient, ayant au préalable activé deux horloges de même facture au même instant t0, ont sur leurs cadrans respectifs exactement la même heure

Ce n'était pas le cas du tout, vous racontez n'importe quoi.

Concernant les jumeaux de Langevin, il semble que ce soit le demi-tour du jumeau qui soit parti dans la fusée qui crée une asymétrie dans le système. Pourtant, vu depuis la fusée, on pourrait aussi dire que c'est le jumeau resté sur terre qui fait demi tour...du coup, y 'a t'il vraiment asymétrie ? Le fait que le jumeau voyageur revient plus jeune n'est-il dû finalement qu'à l'énorme accélération qu'il a subi lors du demi tour? Dans ce cas, seule la RG serait concernée par ce phénomène et pas la RR ?

Autre chose: s'il y a une asymétrie entre les jumeaux, pouvons-nous en conclure qu'une rotation sur soi-même (ou une accélération en général) n'est pas équivalente à une rotation de l'univers tout entier autout de soi? (principe de Mach) Vous voyez ce que je veux dire ? Si le jumeau de la fusée est fortement accéléré lors de son demi tour, selon Mach, il est accéléré par rapport à toutes les masses lointaines, et si j'ai bien compris son principe, cela est équivalent à une accélération de toutes les autres masses de l'univers (dont la terre avec l'autre jumeau dessus) par rapport à lui. Comme cette équivalence ne semble pas vérifiée puisque les jumeaux n'ont pas le même âge après l'expérience de pensée de Langevin, pouvons-nous en déduire que le principe de Mach est faux ?

Hum, ça fait beaucoup de questions en un message, déjà merci à tous pour vos interventions fertiles!

[mach3]

Mais il faudrait commencer par des exercices simples sur les équations de Lorentz.

pas forcément le mieux les transformations de Lorentz pour vraiment comprendre, mais bon, les traditions...

m@ch3

[Merlin95]

Sans vouloir disperser la discussion par rapport aux dernières questions de LLphy, quel outil alors (les diagrammes de Minkowsky peut-être) ?

[mach3]

Concernant les jumeaux de Langevin, il semble que ce soit le demi-tour du jumeau qui soit parti dans la fusée qui crée une asymétrie dans le système. Pourtant, vu depuis la fusée, on pourrait aussi dire que c'est le jumeau resté sur terre qui fait demi tour...du coup, y 'a t'il vraiment asymétrie ? Le fait que le jumeau voyageur revient plus jeune n'est-il dû finalement qu'à l'énorme accélération qu'il a subi lors du demi tour? Dans ce cas, seule la RG serait concernée par ce phénomène et pas la RR ?

Ah! Attention, marronnier!

1ere chose, l'histoire des jumeaux, tant qu'on la raconte en espace-temps plat, relève de RR. Soi-disant la RR ne traiterait que des observateurs en mouvement rectiligne uniforme ? C'est un mythe. Oui les cours de RR pour débutants, où on ne parle que de transformations de Lorentz, de dilatation du temps et contraction des longueurs, et où la métrique de Minkowski est presque passée sous silence ne servent qu'à traiter les MRU. Mais la RR ne s'arrête pas là. Elle est même conçue justement pour traiter des mouvements accélérés, ceux des charges électriques en particulier (l'electrodynamique des corps en mouvement...).

Concernant l'histoire du demi-tour, l'idée revient souvent, mais ce n'est pas ça la solution. On peut imaginer des scénarios biscornus où les deux jumeaux subissent les mêmes accélération et se retrouvent pourtant avec un age différent à la fin, ou inversement, ils ne subissent pas les mêmes accélérations mais finissent au même age. On peut aussi imaginer l'histoire dans un univers type tore et là on peut avoir une différence d'âge sans qu'il n'y ait eu la moindre accélération... Bref, fausse piste.

Il faut s'orienter vers le côté géométrique pour bien comprendre. L'analogie en géométrie euclidienne est l'inégalité triangulaire : la somme des longueurs de deux côtés d'un triangle est forcément plus grande que la longueur du 3e côté.
Dans l'espace-temps de Minkowski, celui de la relativité restreinte, ce n'est pas la métrique d'Euclide qui s'applique, mais celle de Minkowski (qui, en toute rigueur, n'est pas une métrique, mais c'est l'usage de l'appeler ainsi. Il en résulte une géométrie différente, mais qui partage des similitudes avec la géométrie d'Euclide. Il y a notamment une(des) inégalité(s) triangulaire(s).
Dans l'histoire des jumeaux, il y a 3 événements. Leur séparation, A, le demi-tour du voyageur, B et les retrouvailles, C. Pour simplifier, on suppose que le sédentaire est en mouvement rectiligne uniforme entre A et C et que le voyageur enchaîne deux mouvements rectilignes uniformes, entre A et B, puis entre B et C.
On s'intéresse à la "longueur" des côtés du triangle ABC. Ces "longueurs" sont en fait les durées que mesurerait une horloge si elle parcourrait ces côtés. Il vient que la durée entre A et C est différente de la somme des durées de A à B puis de B à C. Si la géométrie était euclidienne, AC serait la plus courte. En géométrie Minkowskienne, il se trouve qu'elle est plus longue dans ce cas de figure (côtés de genre temps et hauteur issue de B de genre espace). Cela peut se démontrer à peu près de la même manière que l'inégalité triangulaire en géométrie d'Euclide.

Pour résumer, l'essentiel de la cinématique de la RR est dans la "longueur" des lignes d'univers (calculable via la métrique de Minkowski) et le fait que physiquement, cette "longueur" est la durée que mesure une horloge qui suit cette ligne d'univers. Si il y a deux lignes d'univers entre deux événements, elles font, sauf cas particulier, une "longueur" différente. Tout comme en géométrie euclidienne : deux courbes entre deux points ont généralement une longueur différente.
C'est ça qu'il est important de comprendre : comment marche la métrique de Minkowski. Les transformations de Lorentz, c'est limite osef, c'est qu'un outil, exactement comme la rotation du plan en géométrie euclidienne.

On parlera de mach demain, il y aussi plein de choses à dire.

m@ch3

[Merlin95]

Mais on peut faire le même raisonnement en disant que c'est le jumeau sur terre qui fait un voyage, celui en mouvement étant considéré au repos.
Les longueurs et les triangles seraient donc ceux du jumeau sur terre, et on trouverait de même que c'est lui qui est le plus âgé.

[Archi3]

oui mais non, puisque le jumeau voyageur change de référentiel galiléen, ce que ne fait pas le jumeau sur Terre.

Il est d'ailleurs illustratif de se demander à quel distance et à quel âge sont chaque jumeau , à chaque phase , vu par chaque autre jumeau.
On peut le faire sur 5 évènements clés du voyage :
* le départ A
* juste avant que le jumeau voyageur fasse son demi tour B
* au milieu du demi tour quand le jumeau voyageur s'est arrêté par rapport à son jumeau terrestre C
* juste après le demi-tour quand le jumeau voyageur repart en arrière D
* à l'arrivée E.

Pour simplifier, on supposera que chaque voyage se fait à gamma= 10, pendant 10 ans pour le jumeau terrestre (20 ans pour aller retour), et que le demi-tour est extrêmement rapide (temps nul à la limite, point anguleux dans le triangle).

Vu du jumeau terrestre J1 , c'est assez simple :

A J1 et J2 ensemble à T=0 , X=0

B J1 = 10 ans à X=0. J2 a voyagé sur 10 a.l (à peu de chose près) mais il n'a vieilli que 1 an
C et D : meme chose que B a peu de chose près. Pendant le demi-tour, (supposé très rapide) J2 ne change ni d'âge ni de position.

E : 10 s'écoulent à nouveau, donc J1 a 20 ans, et J2 n'a que 2 ans. C'est le résultat classique du calcul.


Vu de J2, c'est très très différent et bien plus bizarre !

En A évidemment c'est la même chose.

En B : J2 a toujours 1 an. Le voyage n'a duré que 1 an donc J1 n'est qu'à 1 année lumière de J2 et pas à 10. Comme il a voyagé également à gamma=10, il n'a vieilli que de ... 1/10e d'année soit à peine 1 mois.

Donc J1 n'est qu'a 1 année lumière et n'a vieilli que de un peu plus de 1 mois.

Mais en C , J1 et J2 sont dans le même référentiel donc ils sont d'accord sur les âges et les distances ! donc en C J1 se retrouve brutalement propulsé à 10 années lumières et vieilli de 0,9 ans pour se retrouver à 1 an !
Ce déplacement extraordinairement rapide (superluminique !!) accompagné d'un vieillissement accéléré sera attribué dans un formalisme de RG par un champ de gravitation extrêmement intense , opposé à l'accélération (négative) du jumeau J2. J2 a l'impression d'un champ extrêmement fort qui sépare le jumeau J1 très loin et accélère le temps de J1 par rapport à J2 (c'est J2 qui est ralenti gravitationnellement car il est dans le "puits de potentiel" gravitationnel) . En RR il est interprété comme une variation très rapide (rotation ) du plan de simultanéité . Notons cependant que le jumeau J2 ne "voit" pas le demi-tour de J1 pas plus que J1 ne "voit" instantanément le demi-tour de J2, à cause du temps de parcours fini de la lumière.

ce qui se passe après le demi-tour est mieux compris en analysant la durée du voyage du retour. Il est à nouveau de 1 an pour J2 et à la fin, le jumeau J1 a 2 ans. Juste avant le voyage de retour,J1 était donc à nouveau à 1 année lumière et avait juste 2 ans - 1/10 année soit 1,9 ans. C'est normal car la phase d'accélération est identique à la phase de décélération. J1 prend donc pendant son demi-tour apparent (vu de J2) 2 fois 0,9 ans et effectue un aller retour "accéléré" partant de 1 année lumière, allant jusqu'à 10 a.l. , et revenant à 1 année lumière, avant le voyage de retour qui dure à nouveau 1 an.

Ce demi-tour de J1 par rapport à J2 n'a donc absolument pas les mêmes caractéristiques que celui de J2 par rapport à J1 , qui se faisait à âge et distance pratiquement constante. Ceci est bien sur du au champ de gravitation apparente extrêmement fort qui existe pour J2 et pas pour J1.

[mach3]

Mais on peut faire le même raisonnement en disant que c'est le jumeau sur terre qui fait un voyage, celui en mouvement étant considéré au repos.
Les longueurs et les triangles seraient donc ceux du jumeau sur terre, et on trouverait de même que c'est lui qui est le plus âgé.

non, on ne peut pas. Le segment AC est droit. Le sédentaire ne ressent aucune accélération. Comme il y a un "angle" entre AB et BC, le voyageur ressent une accélération. Les deux lignes sont intrinsèquement différentes, il n'y a pas de symétrie et la présence de l'angle dans ce cas de figure là, implique que AC est plus long.
L'angle, qui est une accélération, peut être vu comme la cause de la différence d'âge aux retrouvailles dans ce cas de figure particulier là, mais son rôle quantitatif est totalement dépendant de la forme de la figure. C'est un tout. Chaque segment de ligne d'univers possède une durée intrinsèque, indépendante du point de vue.
Nul besoin de référentiels ou de systèmes de coordonnées, notions généralement mal comprises de toutes façons.

C'est amusant, le message de Archi3 est illustratif du genre de réponse que je ne veux plus vraiment faire sur ce sujet, à coup de référentiel, de coordonnées.

m@ch3

[mach3]

Vu de J2, c'est très très différent et bien plus bizarre !

En A évidemment c'est la même chose.

En B : J2 a toujours 1 an. Le voyage n'a duré que 1 an donc J1 n'est qu'à 1 année lumière de J2 et pas à 10. Comme il a voyagé également à gamma=10, il n'a vieilli que de ... 1/10e d'année soit à peine 1 mois.

Donc J1 n'est qu'a 1 année lumière et n'a vieilli que de un peu plus de 1 mois.

Mais en C , J1 et J2 sont dans le même référentiel donc ils sont d'accord sur les âges et les distances ! donc en C J1 se retrouve brutalement propulsé à 10 années lumières et vieilli de 0,9 ans pour se retrouver à 1 an !

c'est pas plutôt 10 ans?

ce qui se passe après le demi-tour est mieux compris en analysant la durée du voyage du retour. Il est à nouveau de 1 an pour J2 et à la fin, le jumeau J1 a 2 ans. Juste avant le voyage de retour,J1 était donc à nouveau à 1 année lumière et avait juste 2 ans - 1/10 année soit 1,9 ans.

non, dans le référentiel où le voyageur est immobile pendant la phase de retour, les évènements où J2 à 1 an (D) et où J1 à 19,9 ans ont la même datation.

L'analyse faite en terme de référentiel inertiels successifs peut paraitre très bizarre. Elle semble dire que pour J2, J1 vieilli seulement de 1,2 mois en 1 ans, puis de 9,9 ans instantanément, puis encore de 9,9 ans instantanément, puis de 1,2 mois en 1 ans. Cette analyse est totalement artificielle. Comparer les dates d'évènements séparés par un intervalle spatiale (genre J1 à 1 an et J2 à 10 ans) n'a pas de sens physique, ou si peu. Ce qu'il faut comprendre, à chaque étape, c'est ça :
-Quand le voyageur est en B (avant qu'il ne s'arrête par rapport au sédentaire), alors si une horloge, immobile par rapport à lui, et synchronisée parfaitement à son horloge(*), passe devant le sédentaire alors qu'il a 1,2 mois, elle indiquera 1 an.
-Quand le voyageur est en C (il est immobile par rapport au sédentaire), alors si une horloge, immobile par rapport à lui, et synchronisée parfaitement à son horloge(*), passe devant le sédentaire alors qu'il a 10 ans, elle indiquera 1 an.
-Quand le voyageur est en D (il est à nouveau en mouvement par rapport au sédentaire), alors si une horloge, immobile par rapport à lui, et synchronisée parfaitement à son horloge(*), passe devant le sédentaire alors qu'il a 19,9 ans, elle indiquera 2 ans.
C'est le seul sens physique que l'on peut tirer des datations de référentiels inertiels : la datation d'un évènement distant par rapport à un observateur est l'heure qu'indiquerait une horloge, qui par hasard, passerait par là et serait immobile par rapport à l'observateur et synchronisée avec son horloge. Et ce n'est testable que si on a bien tout prévu au préalable, avec des horloges de mouvements et synchro qui vont bien un peu partout...

Ces datations ne disent pas grand chose sur ce que les jumeaux voient (avec leurs yeux, des perceptions réelles) durant l'expérience et pour le coup ça c'est très physique, mesurable, testable.
Le sédentaire va voir son jumeau au ralenti (car il s'éloigne, effet Doppler) pendant presque 20 ans, l'image qu'il recevra de son jumeau sera celle de ses 1 ans de voyage à la fin de cette phase, puis il verra son jumeau s'arrêter, prenant un rythme "normal", puis enfin, il le verra très accéléré (car il s'approche, effet Doppler), en quelques mois le sédentaire verra son jumeau prendre un an de plus.
Le voyageur va voir pendant 1 an son jumeau au ralenti, sur l'image qu'il recevra de son jumeau à la fin de cette phase, celui n'aura même pas un mois. Il le verra ensuite quelques instant à un rythme normal, puis il le verra très accéléré. Sous les yeux du voyageur, en 1 an, son frère sédentaire va prendre quasiment 20 ans.
Je laisse comme exercice de calculer les ages exacts à chaque étape.

Ce déplacement extraordinairement rapide (superluminique !!) accompagné d'un vieillissement accéléré sera attribué dans un formalisme de RG par un champ de gravitation extrêmement intense , opposé à l'accélération (négative) du jumeau J2. J2 a l'impression d'un champ extrêmement fort qui sépare le jumeau J1 très loin et accélère le temps de J1 par rapport à J2 (c'est J2 qui est ralenti gravitationnellement car il est dans le "puits de potentiel" gravitationnel) .

Alors là, si il y avait un smiley en train de vomir, je l'utiliserais... On est en espace-temps plat. Pas de RG, pas de champ de gravitation (0 courbure).

(*) ce qui signifie ici que si le voyageur effectue une mesure radar sur l'horloge est qu'il obtient une durée 2d, alors l'horloge est à une distance d, et l'heure qu'il voit (avec ses yeux, en vrai) sur cette horloge distante retarde de d par rapport à la sienne. Je considère que c=1, par simplicité.

m@ch3

[Amanuensis]

Je dois avouer être surpris, et en accord avec Mach3. Je ne m'attendais pas à ce genre de phraséologie de la part d'Archi3:

le jumeau voyageur change de référentiel galiléen

Gasp!

Mais en C , J1 et J2 sont dans le même référentiel

Re-gasp, et en plus C est un événement...

Ce déplacement extraordinairement rapide (superluminique !!) accompagné d'un vieillissement accéléré sera attribué dans un formalisme de RG par un champ de gravitation

Gasp encore (un champ d'accélération oui, de gravitation non)

du plan de simultanéité .

Mouais...

---

Dans l'ensemble on voit une phraséologie type mauvaise vulgarisation.

[Amanuensis]

Ah! Attention, marronnier!

Pire que marronier: une ornière de discussion. En gros, quand on tombe dedans la discussion n'en sort plus, et au revoir le sujet initial...

Faudrait une FAQ bien faite, et stopper toute discussion sur les jumeaux avec un renvoi à la FAQ.

[mach3]

bon, au tour de mach maintenant

Autre chose: s'il y a une asymétrie entre les jumeaux, pouvons-nous en conclure qu'une rotation sur soi-même (ou une accélération en général) n'est pas équivalente à une rotation de l'univers tout entier autout de soi? (principe de Mach) Vous voyez ce que je veux dire ? Si le jumeau de la fusée est fortement accéléré lors de son demi tour, selon Mach, il est accéléré par rapport à toutes les masses lointaines, et si j'ai bien compris son principe, cela est équivalent à une accélération de toutes les autres masses de l'univers (dont la terre avec l'autre jumeau dessus) par rapport à lui. Comme cette équivalence ne semble pas vérifiée puisque les jumeaux n'ont pas le même âge après l'expérience de pensée de Langevin, pouvons-nous en déduire que le principe de Mach est faux ?

A l'origine du principe, il y a l'expérience du seau d'eau de Newton, avec la surface de l'eau qui devient concave en cas de rotation axiale du seau. La question est : "si on enlève tout, sauf le seau d'eau, est-ce que la surface de l'eau devient concave quand il tourne ou non?" (on passe sur le fait qu'il faudrait d'abord se demander comment l'eau reste dans le seau, c'est pas la question) ou plus formellement, un objet qui tournerait sur lui même dans un univers vide subirait-il une force centrifuge ou non.
Mach a postulé que non. Que les forces d'inerties sont due à tout le contenu de l'univers et que donc dans un univers avec rien sauf un objet, il n'y a pas de forces d'inertie sur l'objet.
Pendant un moment, Einstein a pensé que sa théorie de la relativité générale était justement en ligne avec ce principe, car un mouvement de chute libre "ici" voit sa forme (la géodésique) dictée par tout le contenu de l'univers, et que du coup, un objet ne suivant pas une chute libre (il ne suit pas une géodésique) subirait une accélération, une force d'inertie, parce qu'il ne suit pas le chemin dicté par le contenu de l'univers. Il pensait même que le principe de mach entrait dans sa théorie comme principe fondateur profond, au même titre que le principe de relativité ou que le principe d'équivalence.
Finalement la RG se construit sans le principe de mach dans ses fondations. La RG semble compatible avec le principe, mais celui-ci n'a pas vraiment d'apport.
Autre chose importante à ce propos, nous n'avons pas d'univers vide sous la main pour tester. Notre univers n'étant pas vide, impossible de savoir si la surface de l'eau est concave quand le seau tourne et qu'on a tout enlever...

Une rotation sur soi, au sens rotation active, n'est pas équivalente à une rotation de tout l'univers autour de soi. On peut facilement savoir qui de soi-même ou du reste de l'univers effectue une rotation active, c'est celui qui subit une force d'inertie. On a tout a fait le droit, "mathématiquement", de compenser cette rotation active sur soi par une rotation passive, ainsi on a une représentation de la situation où on est immobile et où tout le cosmos tourne, mais c'est toujours nous qui subissons la force d'inertie, car dans cette nouvelle représentation, les géodésiques tournent, et ce qui ne tourne pas, ne les suit pas, donc subit une accélération. Attention, c'est un changement de référentiel ou de coordonnées (qui ne sont d'ailleurs pas très bien défini a grande distance dans ce cas de figure...), c'est-à-dire un choix d'étiquetage des évènements, c'est non physique.
Lors du demi-tour, c'est le jumeau voyageur qui subit l'accélération, pas le sédentaire. La situation n'est pas symétrique et chacun peut s'en rendre compte par des mesures ou un ressenti concret.

m@ch3

[LLphy]

Ouf, merci, je vais lire tout ça un peu plus tard, déjà que je commence à traîner sur le forum pendant les heures de boulot .

[Zefram Cochrane]

oui mais non, puisque le jumeau voyageur change de référentiel galiléen, ce que ne fait pas le jumeau sur Terre.

Il est d'ailleurs illustratif de se demander à quel distance et à quel âge sont chaque jumeau , à chaque phase , vu par chaque autre jumeau.
On peut le faire sur 5 évènements clés du voyage :
* le départ A
* juste avant que le jumeau voyageur fasse son demi tour B
* au milieu du demi tour quand le jumeau voyageur s'est arrêté par rapport à son jumeau terrestre C
* juste après le demi-tour quand le jumeau voyageur repart en arrière D
* à l'arrivée E.

Pour simplifier, on supposera que chaque voyage se fait à gamma= 10, pendant 10 ans pour le jumeau terrestre (20 ans pour aller retour), et que le demi-tour est extrêmement rapide (temps nul à la limite, point anguleux dans le triangle).

Vu du jumeau terrestre J1 , c'est assez simple :

A J1 et J2 ensemble à T=0 , X=0

B J1 = 10 ans à X=0. J2 a voyagé sur 10 a.l (à peu de chose près) mais il n'a vieilli que 1 an
C et D : meme chose que B a peu de chose près. Pendant le demi-tour, (supposé très rapide) J2 ne change ni d'âge ni de position.

E : 10 s'écoulent à nouveau, donc J1 a 20 ans, et J2 n'a que 2 ans. C'est le résultat classique du calcul.


Vu de J2, c'est très très différent et bien plus bizarre !

En A évidemment c'est la même chose.

En B : J2 a toujours 1 an. Le voyage n'a duré que 1 an donc J1 n'est qu'à 1 année lumière de J2 et pas à 10. Comme il a voyagé également à gamma=10, il n'a vieilli que de ... 1/10e d'année soit à peine 1 mois.

Donc J1 n'est qu'a 1 année lumière et n'a vieilli que de un peu plus de 1 mois.

Mais en C , J1 et J2 sont dans le même référentiel donc ils sont d'accord sur les âges et les distances ! donc en C J1 se retrouve brutalement propulsé à 10 années lumières et vieilli de 0,9 ans pour se retrouver à 1 an !
Ce déplacement extraordinairement rapide (superluminique !!) accompagné d'un vieillissement accéléré sera attribué dans un formalisme de RG par un champ de gravitation extrêmement intense , opposé à l'accélération (négative) du jumeau J2. J2 a l'impression d'un champ extrêmement fort qui sépare le jumeau J1 très loin et accélère le temps de J1 par rapport à J2 (c'est J2 qui est ralenti gravitationnellement car il est dans le "puits de potentiel" gravitationnel) . En RR il est interprété comme une variation très rapide (rotation ) du plan de simultanéité . Notons cependant que le jumeau J2 ne "voit" pas le demi-tour de J1 pas plus que J1 ne "voit" instantanément le demi-tour de J2, à cause du temps de parcours fini de la lumière.

ce qui se passe après le demi-tour est mieux compris en analysant la durée du voyage du retour. Il est à nouveau de 1 an pour J2 et à la fin, le jumeau J1 a 2 ans. Juste avant le voyage de retour,J1 était donc à nouveau à 1 année lumière et avait juste 2 ans - 1/10 année soit 1,9 ans. C'est normal car la phase d'accélération est identique à la phase de décélération. J1 prend donc pendant son demi-tour apparent (vu de J2) 2 fois 0,9 ans et effectue un aller retour "accéléré" partant de 1 année lumière, allant jusqu'à 10 a.l. , et revenant à 1 année lumière, avant le voyage de retour qui dure à nouveau 1 an.

Ce demi-tour de J1 par rapport à J2 n'a donc absolument pas les mêmes caractéristiques que celui de J2 par rapport à J1 , qui se faisait à âge et distance pratiquement constante. Ceci est bien sur du au champ de gravitation apparente extrêmement fort qui existe pour J2 et pas pour J1.

Alors là, si il y avait un smiley en train de vomir, je l'utiliserais...

Bonjour,
En MRU , un observateur verra l'autre vieillir K fois moins vite que lui s'ils séloignent l'un de l'autre et un observateur verra l'autre vieillir K fois plus vite que lui s'ils se rapporchent l'un de l'autre.
Dans le paradoxe des jumeaux, le voyageur verra le Sédentaire vieillir d'une durée Te = T'/K pendant la phase d'éloignement et d'une durée Ta=K*T' durant la phase d'approche. Le Voyageur verra donc en une duré propre 2T' le Sédentaire vieillir de (K+1/K)*T' = Te + Ta=T.
Le Sédentaire verra en une durée propre Te = K*T' le Voyageur vieillir d'une durée T' pendant la phase d'éloignement et pendant la phase d'approche il verra en une durée propre Ta = T'/K le Voyageur vieillir d'une durée T'.

Donc les deux observateurs seront tous deux d'accord pour affirmer que le Sédentaire aura vieilli d'une durée propre T = (K+1/K)* T' et que el Voyageur aura vielli d'une durée propre 2T' .

L'explication du paradoxe des jumeaux est que le Voyageur est acteur du mouvement à cause du rebond et donc il s'écoule une même durée propre pour lui durant la phase d'éloignement et la phase d'approche tandis que le Sédentaire est spectateur du mouvement et la durée observée d'éloignement est supérieur à celle observée d'approche.

[Merlin95]

non, on ne peut pas. Le segment AC est droit. Le sédentaire ne ressent aucune accélération.

Donc si je résume dans l'analyse géométrique (faite pour comprendre ce qui se passe), on doit conserver l'information de qui ressent l'accélération et c'est pour cela qu'on ne peut pas faire le raisonnement symétrique.

[Amanuensis]

Donc si je résume dans l'analyse géométrique (faite pour comprendre ce qui se passe), on doit conserver l'information de qui ressent l'accélération et c'est pour cela qu'on ne peut pas faire le raisonnement symétrique.

On peut le présenter ainsi. Mais le plus simple argument contre la symétrie est que, comme l'a indiqué Archi3, la description de ce que chacun voit de l'autre est totalement différente. Si l'expérience était faite, ce serait un constat d'observation, et tout modèle devra en rendre compte, et donc être asymétrique.

Il y a tellement d'arguments contre un raisonnement symétrique qu'on se demande pourquoi certains continuent à le défendre. Mais, bon, il y a bien eu un congrès récemment de terre-platistes...

[Nicophil]

Gasp encore (un champ d'accélération oui, de gravitation non).

Un champ de pesanteur.

[Archi3]

c'est pas plutôt 10 ans?

oups pardon, pas bien réveillé, je me suis emmêlé moi meme, oui il a pris 9,9 années pour se retrouver à 10 ans, et encore 9,9 années à la fin du demi tour pour se retrouver à 19,9 années , les dernières 0,1 année étant prises au voyage du retour.

Sinon désolé de vous avoir choqué, mais mon analyse ne voulait démontrer que dans un référentiel galiléen tangent au mouvement de J2, J1 n'avait absolument pas le même mouvement symétrique que celui de J2 vu par J1. En particulier le "demi-tour" de J1 vu par J2 ne peut absolument pas être interprété par une vraie force (comme celle nécessaire pour faire faire demi-tour à J2 , qui est a priori la vraie réaction d'une (rétro) fusée...) . A quoi peut il etre du? uniquement à une "gravité apparente" (ou un champ de forces d'inertie suivant le point de vue). Néanmoins dans un référentiel accéléré type Rindler attaché à J2, c'est bien la différence apparente d'écoulement du temps dans ce champ qui "explique" le vieillissement accéléré de J1 par rapport à J2.

Alors là, si il y avait un smiley en train de vomir, je l'utiliserais... On est en espace-temps plat. Pas de RG, pas de champ de gravitation (0 courbure).

et alors? le redshift gravitationnel ne dépend que de la métrique (le rapport des racines de g00) et pas du tout de la courbure. Il y a un ralentissement du temps apparent dans le référentiel de Rindler dans un espace plat (d'ou l'explication du paradoxe de Bell ou deux vaisseaux ayant la meme accélération propre intrinsèque semble prendre du retard ou de l'avance l'un par rapport l'autre : vu de chaque vaisseau, l'autre parait accélérer moins vite ou plus vite).

sinon pour Amanuensis , j'essaie d'employer un vocabulaire plus correct (ma formulation de ce matin étant un peu "sloppy" ..)

le jumeau voyageur change de référentiel galiléen
Gasp!

"le référentiel galiléen tangent au mouvement du jumeau voyageur change au cours du demi-tour" , ça te va mieux ?

Mais en C , J1 et J2 sont dans le même référentiel
Re-gasp, et en plus C est un événement...

"les référentiels galiléens tangents à J1 (qui est constant) et à J2 au moment de l'évènement C sont les mêmes" : ça te va mieux ?

Ce déplacement extraordinairement rapide (superluminique !!) accompagné d'un vieillissement accéléré sera attribué dans un formalisme de RG par un champ de gravitation
Gasp encore (un champ d'accélération oui, de gravitation non)

question de vocabulaire, mais bien sur dans un référentiel ou J2 est immobile, il y a un champ de "gravitation" ou de "force d'inertie" apparent (connexion non nulle meme si la courbure est nulle)

du plan de simultanéité .
Mouais...

plan de simultanéité dans le référentiel galiléen tangent varie lors du demi -tour .

(PS : la TL montre que le moment "simultané avec vous" à une distance L varie lorsque votre vitesse varie, d'une quantité valant à la limite non relativiste ∆T= ∆V . L/c^2. Rien qu'en marchant de part et d'autre dans une pièce à 1m/s et en se demandant quel instant sur la Galaxie d'Andromede est "simultané" avec vous, on obtient un résultat surprenant...)

[Archi3]

Bonjour,
En MRU , un observateur verra l'autre vieillir K fois moins vite que lui s'ils séloignent l'un de l'autre et un observateur verra l'autre vieillir K fois plus vite que lui s'ils se rapporchent l'un de l'autre.

certainement pas, et dans aucune des interprétations du verbe "voir" ...

[mach3]

certainement pas, et dans aucune des interprétations du verbe "voir" ...

si si, doppler, après ça dépend de ce que vaut K

et alors? le redshift gravitationnel ne dépend que de la métrique (le rapport des racines de g00) et pas du tout de la courbure. Il y a un ralentissement du temps apparent dans le référentiel de Rindler dans un espace plat (d'ou l'explication du paradoxe de Bell ou deux vaisseaux ayant la meme accélération propre intrinsèque semble prendre du retard ou de l'avance l'un par rapport l'autre : vu de chaque vaisseau, l'autre parait accélérer moins vite ou plus vite).

On est en espace-temps plat, courbure 0, donc on ne parle pas de RG, c'est tout. On est en plein dans la RR, la belle RR, la vraie, bien rude avec des observateurs accélérés . Ca n'empêche pas qu'il y ait un redshift qui mime le redshift gravitationnel de la RG dans un référentiel uniformément accéléré, cause principe d'équivalence, et c'est même un résultat tout à fait intéressant et instructif.

m@ch3

[Merlin95]

On peut le présenter ainsi. Mais le plus simple argument contre la symétrie est que, comme l'a indiqué Archi3, la description de ce que chacun voit de l'autre est totalement différente

Ok je vais relire à tête reposée.

Il y a tellement d'arguments contre un raisonnement symétrique qu'on se demande pourquoi certains continuent à le défendre. Mais, bon, il y a bien eu un congrès récemment de terre-platistes...

J'avoue avoir du mal à assimiler la non pertinence du raisonnement symétrique. Plutôt un manque de pratique (on va dire ca).

[Amanuensis]

Ca n'empêche pas qu'il y ait un redshift qui mime le redshift gravitationnel de la RG dans un référentiel uniformément accéléré, cause principe d'équivalence, et c'est même un résultat tout à fait intéressant et instructif.

Faut que je retrouve l'article, mais c'est bien plus que mimer. Les trois phénomènes de redshift (effet RR de vitesse, effet gravitationnel, décalage cosmologique) et évidemment leurs combinaisons se résument à une combinaison d'un transport parallèle et d'un angle entre qvecteurs (entre le U du récepteur et le V' au point de réception, transporté du V de l'émetteur). C'est essentiellement la même chose, pas l'un qui mime l'autre.

D'ailleurs ce sont les combinaisons les plus intéressantes: car elles montrent qu'il n'y a pas moyen de distinguer les causes. Les trois effets sont distingués parce qu'apparaissant «purs» resp. dans les modèles «essentiels», ceux dont on parle en permanence : l'espace-temps de Minkowski (effet de la vitesse seule), géométrie extérieure de Schw. (décalage gravitationnel), et modèle cosmologique FLRW (décalage cosmologique). Chacun ont la particularité d'avoir des référentiels privilégiés qui «isole» un des effets.

Mais si on prend un cas totalement général, alors on ne peut pas décomposer, mais l'approche par le transport parallèle marche toujours.

Dans le cas accéléré en RR, c'est le qvecteur de la cible qui tourne par rapport à l'inertiel. Dans les cas Schw. et cosmologique, c'est a géométrie de l'espace-temps qui fait tourner le qv transporté.

Notons aussi que l'approche par le transport est indépendante du référentiel ou des coordonnées, c'est une description géométrique.