Bonjour,
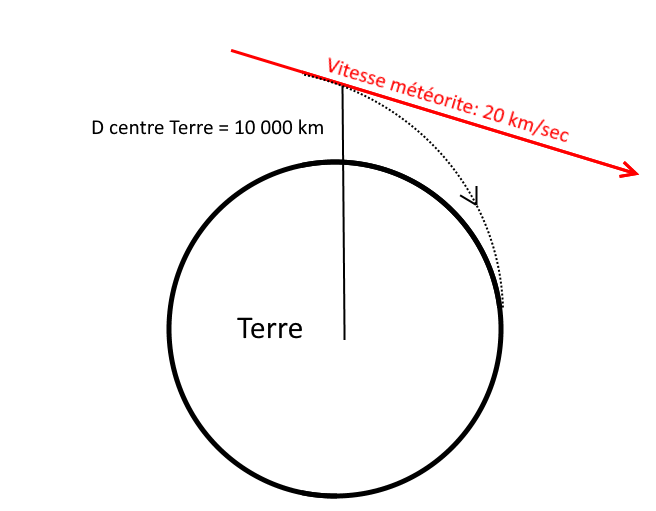
lorsqu'une météorite se déplace en direction de la Terre puis la tangente.
Est-ce qu'en connaissant la vitesse initiale de la météorite et sa distance à la Terre, on peut calculer de combien sa trajectoire sera modifiée.
Merci pour vos explications.
En connaissant vitesses et positions initiales des objets, on peut en principe tout calculer.Envoyé par Youri Gagarine
Mais en mécanique céleste où 3 corps ou plus interviennent (dans ton exemple, à minima, une météorite, la Terre, le Soleil), ca devient rapidement hors de portée de calculs à la main, il faut des modèles numériques.
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
restons simples, on va juste rester dans mécanique à 2 corps.
Mais je ne sais pas par quoi commencer.
Cependant l'énergie cinétique d'une météorite de 1kg, vitesse 30 km/sec est 45 millions de fois plus élevée que l'attraction terrestre.
Donc est ce que la gravité terrestre pourrait modifier la trajectoire de cette météorite?
Bonjour,
C'est facile : https://fr.wikipedia.org/wiki/Probl%...%A0_deux_corps
Petit soucis de définition et de vocabulaire ici.
La gravité terrestre ne modifie pas la trajectoire, puisque le système que vous considérez est constitué de la Terre et de la météorite. L'attraction gravitationnelle entre les deux corps défini la trajectoire (des deux).
Not only is it not right, it's not even wrong!
Comment faites vous pour comparer une énergie cinétique et une accélération ?
En plus de la réponse d'Albanxiii, la gravité terrestre influe sur tous les corps de l'Univers (avec des nuances sur la vitesse de la lumière mais on va rester simple).
Donc dans le sens où vous l'entendez, elle va influer sur votre météorite. Mais il faudrait aussi se demander à quelle distance elle est. Si elle se promène au delà de Pluton et qu'on se place dans un référentiel héliocentrique, l'influence de la Terre sera faible.
Si elle passe à 300 km, elle sera déviée sensiblement.
Salut,
C'est une correction purement de terminologie, mais une meteorite qui ne tombe pas sur la Terre n'est pas une meteorite. Cela reste un asteroide
Une meteorite est un caillou trouve sur Terre (ou sur une autre planete/satellite) provenant d'un astre different (asteroide, planete, etc.).
T-K
If you open your mind too much, your brain will fall out (T.Minchin)
Oui effectivement!
J'ai dit un peu n'importe quoi là!
Ma question porte sur les objets arrivant dans l'environnement terrestre. A partir du moment où ils subissent une influence qui va modifier leur trajectoire.
Tu as raison de me corriger.Salut,
C'est une correction purement de terminologie, mais une meteorite qui ne tombe pas sur la Terre n'est pas une meteorite. Cela reste un asteroide
Une meteorite est un caillou trouve sur Terre (ou sur une autre planete/satellite) provenant d'un astre different (asteroide, planete, etc.).
T-K
Mais je ne suis pas sûr qu'on utilise le terme "astéroïde" pour un caillou de quelques centaines de grammes en orbite autour du soleil.
Est ce qu'on peut utiliser le terme "objet"?
Donc, à partir de quand la trajectoire d'un objet se déplaçant à 30 km/sec sera modifiée par l'attraction gravitationnelle de la Terre?
La réponse a été donnée. Tu devrais lire ce que les participants écrivent quand tu poses une question.
Mais non! Ou alors on ne s'est pas compris.
Au début, le corps est uniquement soumis à l'attraction gravitationnelle du soleil, il est en orbite autour du soleil.
Et s'il passe suffisamment proche de la Terre, alors il s'agira d'un problème à 3 corps: soleil/terre/objet
Salut,
On peut faire plus simple, inutile de se torturer l'esprit.
1) considérer la trajectoire de la météorite en l'absence de la Terre
2) considérer la trajectoire en présence de la Terre
Et là on peut parler de déviation par la Terre sans se faire des nœuds dans la tête
Pour le problème à trois corps, gasp, compliqué. A éviter sauf accès à un calculateur.
Je propose plutôt d'utiliser 1 loin de la Terre
Puis de considérer la trajectoire comme une condition initiale, faire un changement de repère pour avoir une terre immobile et considérer le mouvement de l'astéroïde dans le champ des deux masses immobiles. Et à la fin, hop, retour au référentiel héliocentrique.
Bon, ne faisons pas "yaka", ça reste des calculs assez costauds.
Avec ça tu peux même calculer les effets de frondes
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
C'est bien compliqué tout cela!
Ma question est très simple:
Considérant un objet qui se déplace en ligne droite (météorite, ou balle de fusil, ou balle de tennis), on connait sa vitesse, comment est ce qu'on calcule l'angle de déviation de l'objet, causé par l'attraction terrestre.
Bonjour, je reviens après plus d'un an et demi sur ce sujet qui me tracasse, en vous rajoutant un schéma.
Connaissant la vitesse de la météorite, donnée par rapport au référentiel terrestre.
Sa distance minimum au centre de gravité de la Terre.
L'angle de la trajectoire de cette météorite.
Comment est ce qu'on calcule le point d'impact de la météorite sur Terre?
J'ai l'impression que cela revient à étudier un simple calcul balistique?
Merci pour votre aide.
Youri.
Bonjour,
C'est en effet un simple calcul balistique mais avec g variable.
Vous avez une trajectoire newtonienne, pour laquelle vous connaissez parfaitement l'un des points.
Vous pouvez calculer l'énergie, ce qui vous donnera le grand axe 2a (en supposant que cela soit une ellipse).
Vous pouvez calculer la constante de la loi des aires, ce qui vous permettra de calculer le paramètre p.
En reportant dans l'énergie vous obtiendrez l'excentricité e.
A partir de là vous connaissez l'équation de la trajectoire.
En reportant dans cette équation, vous obtiendrez l'angle repérant la position θ0 par rapport au grand axe.
Et enfin en résolvant R(terre)=r(θ(terre)), vous obtiendrez la position du point d'impact.
Merci pour la réponse, mais j'ai pas le niveau pour tout comprendre, est ce que vous êtes d'accord pour m'aider à comprendre pas à pas?
Est ce que j'utilise F=G.M.m/r²?
merci
Pour ce qui est de l'énergie, je parle bien d'énergie, pas de forces.
Si vous ne connaissez pas les orbites newtoniennes, je m'appuie sur les résultats connus sur celles-ci, je ne repart pas de zéro, c'est un cours entier...
Remarque : je n'ai pas fait les calculs numériques et suis parti sur l'idée d'une trajectoire elliptique, à voir... (Si vous trouver E>0, il faudra reprendre)
Energie= énergie cinétique + potentielle
, ce qui donne 2a est le grand axe de l'ellipse
Moment cinétique
Un grand merci pour le détail. Est ce que vous pourriez juste m'expliquer ceci:Energie= énergie cinétique + potentielle
Moment cinétique
Le
Merci et désolé pour mes questions de débutants!
Bjr à toi,
Le point d'impact (lieu du choc) va dépendre de la position de la terre (rotation de la terre) à l'heure
considérée de l'impact.
Donc faut aussi CONNAITRE la position de la terre à l'heure du choc.
Bonne journée
Salut,
Non c'est juste r * v.
Oui.Le
C'est l'excentricité, par le nombre népérien. https://fr.wikipedia.org/wiki/Excent...C3%A9_orbitale
Ca dit juste si l'orbite est circulaire ou plus ou moins elliptique.
P.S. j'ai de bizarres petits soucis avec LaTex Mes formules n'apparaissent pas.
Dernière modification par Deedee81 ; 30/06/2020 à 07h03.
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Merci pour les réponses, ça se clarifie, je vais pouvoir passer tout ça sur tableur.
Moi je les vois parfaitement.
Salut,
Maintenant moi aussi. Bizarre.
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Bonjour,
Si on part des données numériques du message 13 ... on peut déjà être sûr que la trajectoire ne pourra pas être une ellipse ... il ne faut donc pas partir de cet a priori pour faire des calculs.
En effet : Em = m * (-GM/do + 1/2 Vo²) = m * (-6,67.10^-11 * 5,98.10^24/10000000 + 1/2 * 20000²) > 0 et donc la trajectoire sera une branche d'hyperbole ... qui pourra ou non aboutir à un crash.
Autrement : la vitesse de 20 km/s est supérieure à la vitesse de libération de l'attraction terrestre ... et donc, soit il y aura un crash, soit la trajectoire sera une branche d'hyperbole.
Si on veut se servir d'un tableur, on peut le faire sans aucun a priori sur la nature de la trajectoire.
Dans le plan de la trajectoire du météorite contenant le centre le Terre (réflexion limitée à 2 corps) pris comme centre du repère.
Avec la droite dessinée verticale sur le dessin du message 13 comme axe des ordonnées et la perpenpiculaire à l'axe des ordonnées passant par le centre de la Terre comme axe des abscisses.
A partir du point initial de la position du météorite ((0 ; 10000000) sur le dessin ... mais qu'on peut évidemment modifier)
et à partir de la vitesse "initiale" (20000 m/s sur le dessin ... mais qu'on peut évidemment modifier)
et à partir de l'angle fait par la vitesse en t = 0 avec l'axe des ordonnées ...
On calcule aisément Vx(0) ; Vy(0) et on calcule |F| = GmM/sqrt(x²+y²) et on en déduit les accélérations suivant les axes : ax = GM*x/(x²+y²)^(3/2)
et ay = -GM*y/(x²+y²)^(3/2)
Et par incréments de temps successifs ... on peut donc calculer V(x) ; V(y) , x et y en fonction du temps
On trace ainsi la trajectoire (dans le plan défini) et on peut tracer sur le même graphe le profil de la Terre.
Voila par exemple ce que cela donne avec les données du dessin message 13 ... et avec un angle de 60° entre la "verticale" et le vecteur vitesse quand le météorite coupe l'axe des ordonnées.
(dessin de gauche)
Et avec les même données ... sauf angle de 30° au lieu de 60° (à droite)
