Je vais essayer d’être plus concret que dans mon précédent message .
Donc vitesse au sommet : conservation de l’énergie d’où
m.g.(h1-d) = 1/2 m.vs avec m = 0.03 kg h1 = 0.93 m d = 0.23 m
vs = sqrt( 2.g (h1- d)) vs = sqrt( 2 * 9.81* 0.7) = 3.70 m/s
Force centrifuge au sommet m. vs^2/ d/2 = 2 m.vs^2 /d = 2*0.03*(3.7)^2/0.23 = 3.57 N
Poids m.g = 0.03 *9.81 = 0.294 N
Donc si la voiture part du haut de la rampe il y a une très grosse marge.
Si on veux être très rigoureux on doit justifier que vs est la bonne vitesse à utiliser.
Dans la montée Vm > vs (conservation de l'énergie) et le poids est projeté sur le rayon donc avec un sin(teta) < 1 . Poids plus petit, force centrifuge plus grande CQFD
Même chose pour la descente.
Pour « pinailler" :
1)Le centre de gravité n’est pas au niveau de roue d'où une variation de l’énergie potentielle. Refaire le calcul avec un diamètre plus petit tenant compte de la distance roue / centre de gravité
2)La force d’appui au sommet ne doit pas être nulle ou un peu positive. Il faut un minimum d’adhérence de force d’appui sinon ça part dans le décor. La valeur maxi est le poids puisque ça marche sur une trajectoire normale.
Les frottements : en général pour les forces de roulement on prends F = alpha * v Pour la résistance de l'air F = ½ Ro v^2 Cx avec Ro densité de l'air Cx facteur de trainée.
Mais cela conduit souvent à des équations différentielles qui n'ont pas de solution analytique. (Possible que l'équation donnée dans le brouillon en fasse partie). Reste le calcul numérique avec les méthodes itératives.
-----





 ; pour le cercle, l'accélération est supérieure à g (à cause de l'action de la glissière)
; pour le cercle, l'accélération est supérieure à g (à cause de l'action de la glissière) 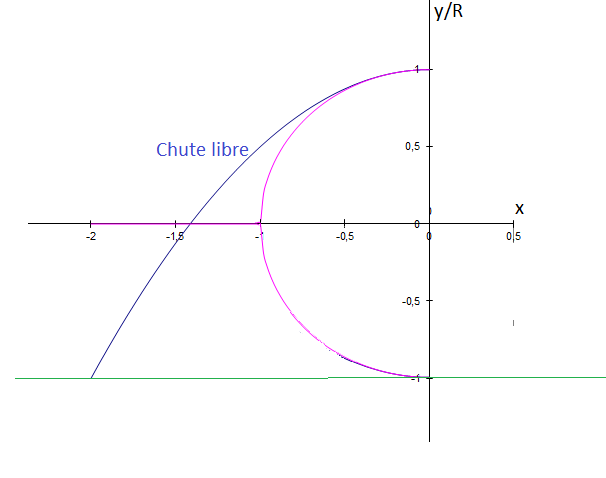
 Pub
Pub