Rotation ou translation ?

[Christian Arnaud]

Amis de la statique , bonjour



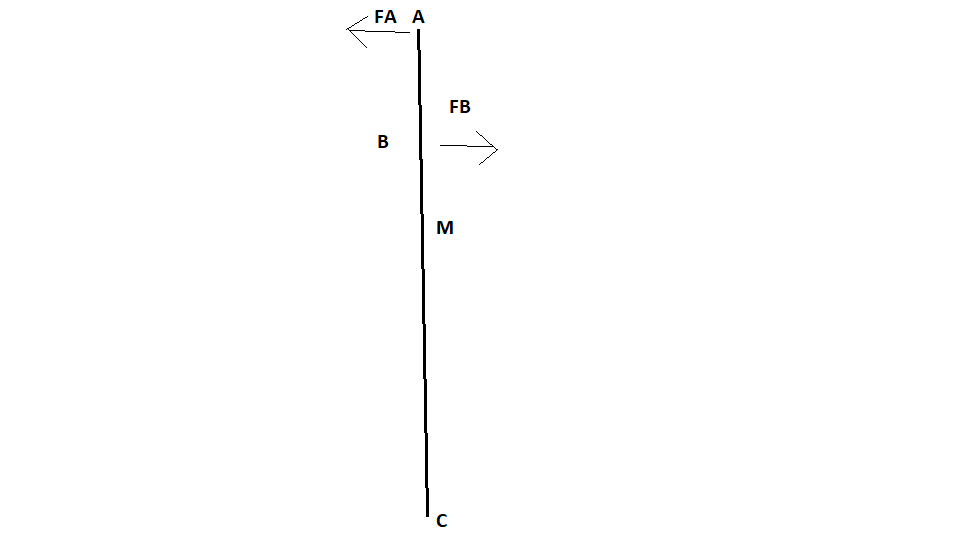
Le schéma ci-dessus représente une barre homogène de section rectangulaire AC , de centre de gravité M. Elle repose à plat sur une plaque horizontale de faible adhérence. Elle subit l'action de deux forces opposées :
- FA en A vers la gauche
- FB en B vers la droite
Les modules des deux forces ne sont pas égaux et on AB=1/5(AC) ( le point B est situé au 1 5ème de la barre AC)

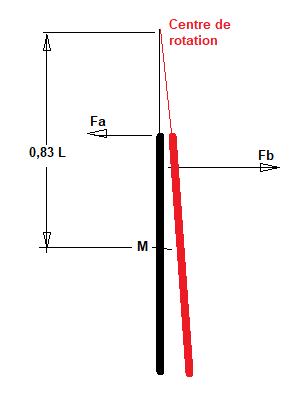
1) Suivant les modules des deux forces, y-aura-t-il rotation ou translation de la barre ou les deux ?

2) Comment tenir compte de l'adhérence (ou frottement) entre la barre et la plaque , et cela influe-t-il sur le mouvement obtenu ?

D'avance merci
-----

[Dynamix]

Salut

1) Suivant les modules des deux forces, y-aura-t-il rotation ou translation de la barre ou les deux ?

Il faut distinguer 3 cas :
_Cas général
_Résultante nulle
_Moment nul en M
(En plus du cas "moment nul en tout points")

[harmoniciste]

Bonjour,
Vous devez considérer le moments la somme des moments des 2 forces par rapport à M: Fa* AM - Fb* BM
Cette somme produira une rotation autour de M, d'accélération égale à 3 (Fa* AM - Fb* BM) / (masse * AC²)

De plus, le point M subira l'accélération linéaire Acc, due à la la somme des forces appliquées:
Acc = (Fa - Fb) /masse

[Sethy]

Bonjour,

Question : après déplacement, est-ce que les force Fa et Fb restent "horizontales" ou au contraire restent-elles "perpendiculaires" à la barre ?

Question subsidiaires : Ces forces sont elles exercées par une attraction (aimantation) ou par un asservissement mécanique à la barre ?

Cela ne change évidemment rien au déplacement initial, mais cela à des conséquences pour la suite.

[A voir en vidéo sur Futura]

[Christian Arnaud]

Bonjour,
Vous devez considérer le moments la somme des moments des 2 forces par rapport à M: Fa* AM - Fb* BM
Cette somme produira une rotation autour de M, d'accélération égale à 3 (Fa* AM - Fb* BM) / (masse * AC²)

De plus, le point M subira l'accélération linéaire Acc, due à la la somme des forces appliquées:
Acc = (Fa - Fb) /masse

Merci , harmonisiste ; mais la rotation a -t-elle bien lieu autour de M ou entre A et B ? (au centre de gravité de la section AB )

[Christian Arnaud]

Bonjour,

Question : après déplacement, est-ce que les force Fa et Fb restent "horizontales" ou au contraire restent-elles "perpendiculaires" à la barre ?

Question subsidiaires : Ces forces sont elles exercées par une attraction (aimantation) ou par un asservissement mécanique à la barre ?

Bonjour Sethy .
les forces A et B restent horizontales (elles viennent d'un asservissement mécanique dans un mécanisme d'horlogerie Atmos). Mais le cas inverse ( forces restant perpendiculaires exercées par une aimantation) m'intéresse aussi

[harmoniciste]

La rotation n'est qu' un changement angulaire de la barre. Il n'est donc pas question de centre de rotation.
Un centre de rotation ne peut être localisé qu'en fonction de la translation du centre de gravité M
Si, dans un court intervalle de temps, le centre de gravité est déplacé et que la position angulaire de la barre est modifiée, il apparait qu'un point de la barre reste pratiquement immobile: C'est là le centre instantané de rotation.

[Christian Arnaud]

Salut


Il faut distinguer 3 cas :
_Cas général
_Résultante nulle
_Moment nul en M
(En plus du cas "moment nul en tout points")

Bonjour ,

Et comment poursuit-on , par exemple dans le cas général ?

[Christian Arnaud]

=harmoniciste;6384792]La rotation n'est qu' un changement angulaire de la barre. Il n'est donc pas question de centre de rotation.
Un centre de rotation ne peut être localisé qu'en fonction de la translation du centre de gravité M
Si, dans un court intervalle de temps, le centre de gravité est déplacé et que la position angulaire de la barre est modifiée, il apparait qu'un point de la barre reste pratiquement immobile: C'est là le centre instantané de rotation.

Sans doute , mais si M reste fixe , il y a bien une rotation , non ?

[Resartus]

Bonjour,

Comme indiqué par harmoniciste, c'est une question de dynamique. Il n'y a centre instantané de rotation que si la barre bouge

Dans le cas simple où le frottement est nul, on peut écrire l'accélération du centre de gravité de la barre et son accélération angulaire en fonction des forces et de leurs moments, de la masse de la barre et de son moment d'inertie (1/12 ml² si on suppose qu'elle est homogène et de faible largeur)
En intégrant sur les premières fractions de seconde, cela donne une vitesse angulaire et une vitesse de rotation proportionnelles au temps, et le rapport entre les deux va donner la position du centre instantané de rotation
Pas le courage d'écrire la solution générale, mais voici quelques cas simples :

Si FB=-FA la barre tournera autour de son centre de gravité
Si FB=0, elle tournera autour d'un point situé à l/6 du centre de gravité du coté opposé à FA (c'est à dire au 2/3 de la barre)

[Dynamix]

Et comment poursuit-on , par exemple dans le cas général ?

Avec le PDF , comme d' hab

Sans doute , mais si M reste fixe , il y a bien une rotation , non ?

Si M seul reste fixe , oui .

[Resartus]

Bonjour,
Pour ce qui est du cas avec frottement, cela devient un peu plus compliqué :

au moment précis où cela commence à bouger, les forces de frottement sont au maximum c'est à dire f*mu*g par unité de longueur (où mu est la masse linéique de la barre), mais elles sont orientées à l'opposé de FA-FB d'un coté du centre de rotation, et dans le même sens que FA-FB de l'autre coté.
Cela donne une résultante et un moment résultant qui vont dépendre de la position du centre de rotation, et qu'il faudra rajouter aux deux équations du PFD puis résoudre pour trouver la position de ce centre de rotation

[Christian Arnaud]

Si FB=-FA la barre tournera autour de son centre de gravité
Si FB=0, elle tournera autour d'un point situé à l/6 du centre de gravité du coté opposé à FA (c'est à dire au 2/3 de la barre)

Si FB=-FA la barre tournera autour de son centre de gravité
Si FB=0, elle tournera autour d'un point situé à l/6 du centre de gravité du coté opposé à FA (c'est à dire au 2/3 de la barre)

Bonjour Resartus et merci pour ces explications

Pourrais-tu rajouter stp où est le centre instantané de rotation dans le cas où FB=-2FA ? Merci

[Christian Arnaud]

Avec le PDF , comme d'hab

PDF ou PFD ?

[harmoniciste]

Avec Fb = -2 Fa et AB = AC/5, on a
Somme des moments autour de M: Fa*L/2 - Fb(3L/10) = Fa *L/10,
donnant l'accélération angulaire : Fa * L/10 / ( m L^2/12) ou 1,2 Fa / m L
On a aussi l'accélération de M = -Fa /m
Le centre instantané de rotation étant fixe par définition implique que la vitesse du déplacement de ce point, dûe à la translation de M (1), et égale et opposée à celle due à la rotation autour de M (2).
Or (1) vaut -(Fa/m)*t ou -K*t en prenant K = Fa/m
et (2) vaut X*(1,2 K L)*t (avec X =distance séparant M du centre de rotation)
on a alors K = K*X*1.2 L D'où X/L = 1/1,2 = 0.83 L

[Christian Arnaud]

on a alors K = K*X*1.2 L D'où X/L = 1/1,2 = 0.83 L

Merci harmoniciste pour le résultat et pour avoir fait l'effort d'en donner le détail et aussi pour avoir pris le temps de faire un schéma clair et propre (beaucoup mieux que le mien)