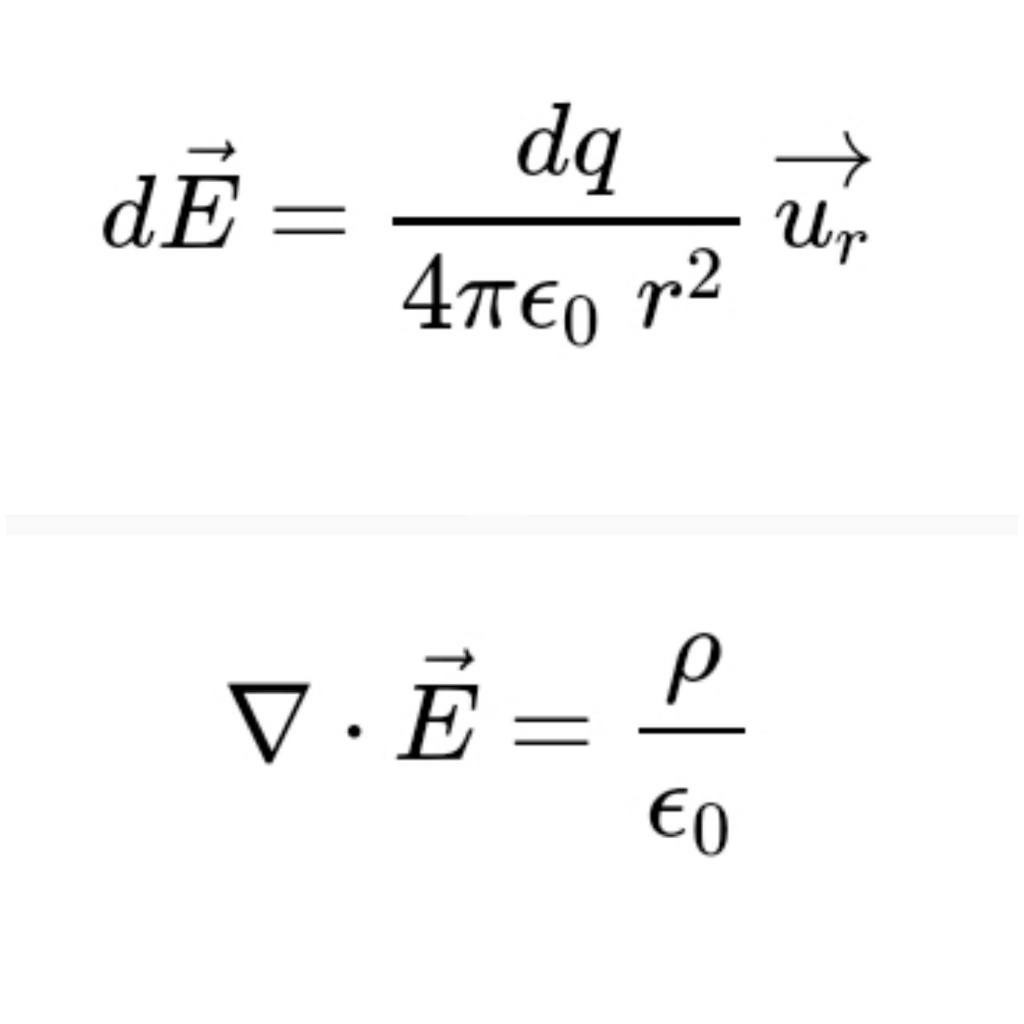Établir l'équation de Maxwell-Gauss à partir de la loi de Coulomb

[langcheuv]

Bonjour,

Il s'agit peut être plus d'un problème mathématique mais bon...
J'aimerais établir proprement l'équation de Maxwell-Gauss sous forme locale en partant de la loi de Coulomb. Bien sûr sans utiliser de théorèmes (Green-Ostrogradsky ou autres).

Merci poir votre aide.
-----

[langcheuv]

Quelqu'un passant par là, peut être ?

[phys4]

La loi de Coulomb contient une terme en inverse du carré de la distance, qui permet de prouver que le flux du champ électrique à travers une sphère entourant une charge est toujours
Vous pouvez prouver aussi que le flux dans un cône ayant pour sommet la charge ne dépend que de l'angle solide du cône. Le flux total dans l'ensemble des cônes autour de la charge est donc également , et ce flux ne dépend pas de la forme de la surface entourant cette charge. Une charge extérieur donnera un flux total nul.

Vous devriez pouvoir en déduire que le flux sortant d'une surface quelconque est proportionnel à la somme des charges intérieures.

[langcheuv]

Bonjour,

Votre raisonnement sous-entend le théorème de Gauss. Je veux justement partir de la loi de Coulomb pour en déduire l'équation de Maxwell-Gauss par calcul direct.

[A voir en vidéo sur Futura]

[phys4]

La loi de Coulomb vous donne la fonction de l'inverse du carré de la distance, c'est ce qui permet de définir un flux constant dans un angle solide.

Je ne vois pas de chemin plus direct ?

[langcheuv]

Je vois, merci. J'ai vu des débuts de démonstrations qui ne faisaient pas intervenir la notion d'angle solide, mais les calculs semblaient techniques.

[0577]

Bonjour,

J'aimerais établir proprement l'équation de Maxwell-Gauss sous forme locale en partant de la loi de Coulomb.

Une première étape serait de formuler proprement ce que vous appelez "loi de Coulomb" et "équation de Maxwell-Gauss".

[soliris]

Bonjour,

A cet endroit sur Futura-sciences, j'ai trouvé ceci:

[soliris]

Whoups, j'avais écrit 2 x le même message, mille excuses.

[gts2]

Je veux justement partir de la loi de Coulomb pour en déduire l'équation de Maxwell-Gauss par calcul direct.

En partant de quelle définition de la divergence ?

[langcheuv]

Je veux donc partir de la loi de Coulomb, pour arriver à la forme locale de l'équation de Maxwell-Gauss.

[ThM55]

D'habitude on fait la déduction dans l'autre sens car on va plus naturellement du général au particulier que du particulier au général. Mais dans le cas particulier, les deux lois sont équivalentes.

Dans le cas particulier d'une charge ponctuelle à l'origine, on peut écrire la distribution de charge sous la forme d'une distribution de Dirac .

La loi de Maxwell s'écrit alors .

A partir de là je ne vois pas comment on peut se passer du théorème de la divergence, ou théorème de Green-Ostrogradski. Pourquoi faudrait-il s'en passer? Pour la fierté d'être ignorant?

Ce théorème nous dit que l'intégrale de la divergence d'un champ de vecteurs sur un volume de l'espace est égal au flux de ce vecteur à travers la frontière de ce volume. Si pour le volume je prends une sphère centrée à l'origine, j'obtiens immédiatement la loi de Coulomb car l'intégrale du delta donne .

Maintenant, si je pars de la loi de Coulomb, je dois démontrer que la divergence du champ de vecteurs est un delta.

Essayons. Avec la convention d'Einstein (indices répétés sont sommés) cette divergence peut s'écrire et . On calcule alors facilement la divergence (ici ):



Mais

et


En substituant on trouve:
.

Si , le résultat est nul. La divergence est bien nulle partout sauf peut être à l'origine. Plaçons une petite sphère centrée à l'origine et de rayon . Il est clair que le flux du champ électrique à travers cette sphère est . Donc d'après le théorème, l'intégrale de la divergence sur le volume de cette sphère a cette valeur non nulle. Pourtant elle est nulle partout sauf à l'origine. Donc elle doit être proportionnelle à la distribution de Dirac.
CQFD

[ThM55]

Pour compléter la démonstration et obtenir la loi de Maxwell-Gauss pour toute distribution de charges et non plus seulement pour une seule charge ponctuelle, il faut postuler que le champ obtenu est la somme des champs de Coulomb de chaque élément de volume. Autrement dit que l'équation de Maxwell est linéaire. En sommant les distributions de Dirac on trouve au second membre la distribution de charges générale.

[0577]

Bonjour,

d'après le théorème, l'intégrale de la divergence sur le volume de cette sphère a cette valeur non nulle. Pourtant elle est nulle partout sauf à l'origine. Donc elle doit être proportionnelle à la distribution de Dirac.
CQFD

Ce dernier "donc" n'est pas justifié: si l'on ajoute à la distribution de Dirac un multiple non-nul de sa dérivée, on obtient une distribution nulle partout sauf à l'origine, d'intégrale 1 sur le volume d'une sphère autour de 0, et qui n'est pas proportionnelle à la distribution de Dirac (physiquement, si l'on ajoute un moment dipolaire à une particule ponctuelle, on ne change pas la charge, la divergence du champ électrique reste nulle en dehors de la particule, et pourtant le champ électrique change). L'argument est donc incomplet en l'état.

[ThM55]

Bonsoir. Non, un tel terme de dérivée est exclu du fait de la symétrie sphérique qui se trouve dans l'hypothèse de départ (champ coulombien). On doit obtenir un scalaire pour l'égaler à la divergence, pour cela il faudrait par exemple faire le produit scalaire du gradient avec un vecteur fixé dans une direction donnée et cela privilégie cette direction. Mais vous avez raison, il faut le dire pour que la preuve soit complète.

[0577]

un tel terme de dérivée est exclu du fait de la symétrie sphérique qui se trouve dans l'hypothèse de départ (champ coulombien).

Oui!

Pour poursuivre dans le pinaillage: il faudrait démontrer que la distribution de Dirac est la seule distribution supportée en un point et avec symétrie sphérique. C'est en effet clair si l'on sait qu'une distribution supportée en un point est une combinaison linéaire de dérivées de la distribution de Dirac, mais encore faudrait-il démontrer aussi cela...

Là où je veux en venir est qu'il faudra à la fin écrire la définition d'une distribution et ce sera une réponse à la question initiale sur l'utilisation du théorème de Gauss (=de la divergence=Green-...): dans le monde des distributions, la dérivée est définie par une intégration par parties formelle, et le théorème de Gauss n'étant qu'une version de l'intégration par partie, il n'est pas étonnant qu'il apparaisse puisqu'il était en un sens caché dans la définition de la divergence.

Une autre manière un peu moins tautologique de répondre à la question initiale serait de s'interdire de parler de distribution mathématique, en partant d'une distribution de charges suffisamment dérivable et en interprétant la loi de Coulomb comment donnant le champ électrique créé sous forme intégrale. La version non-tautologique de la question est alors de montrer que ce champ électrique est suffisamment dérivable, et que sa divergence, définie honnêtement en termes de dérivées, est donnée par l'équation de Maxwell-Gauss.

[phys4]

Je n'avais compris que l'auteur voulait la relation locale avec la divergence de E. Aussi j'ai donné seulement comment obtenir la relation intégrale du flux à travers une surface.

Pour obtenir directement la relation locale sans passer par la distribution de Dirac, il faudrait utiliser une sphère uniformément chargée en volume.
Il sera alors possible de montrer que la divergence est nulle hors de la sphère, constante et égale au rapport à l'intérieur de la sphère.

Si vous voulez éviter la formule de divergence en sphérique, vous pouvez calculer le champ d'un plan infini uniformément chargé. Puis utiliser cette formule pour calculer le champ d'une plaque épaisse.
La divergence est alors très simple, et vous retrouvez une divergence nulle à l'extérieur de la plaque et la divergence constante à l'intérieur.

[ThM55]

En réponse à 0577: il n'est pas difficile de rendre cet argument parfaitement rigoureux avec la théorie des distributions. Je n'ai pas la patience pour développer cela ici en LATEX et l'argument serait considérablement alourdi et n'aurait de sens que si le questionneur est suffisamment versé en théorie des distributions. Schématiquement, il "suffit" de régulariser le potentiel coulombien en déplaçant les pôles, puis d'intégrer la divergence avec une fonction test f et de montrer que l'intégrale tend vers une grandeur proportionnelle à f(0) et enfin de prendre la limite quand les pôles reviennent en zéro. Cela prouve rigoureusement que la distribution est celle de Dirac. Il faut justifier chaque étape avec toutes sortes de conditions techniques nécessaires pour prendre la limite. Je pense que tous les physiciens savent qu'il faut faire cela mais préfèrent s'en passer car cela n'a rien d'essentiel pour le résultat physique. Et tant qu'on ne me provoque pas en duel je ne sors pas les armes lourdes.

Un exemple réel: dans leur livre "Gravity - Newtonian, Post-Newtonian, Relativistic", Eric Poisson et Clifford Will (deux sommités en relativité générale), écrivent page 9 un encadré "Proof that . Cela concerne le potentiel newtonien, mais c'est exactement le même argument que celui que j'ai développé. Il concluent après un calcul semblable au mien: "(...) the surface integral returns -4 Pi. Because (the laplacian) vanishes when whenever the integration domain encloses x=0, we conclude that it is distributionally equal to ." C'est le niveau de rigueur normal dans un traité de physique semble-t-il.

Toutefois, si j'ai l'occasion de parler à Eric Poisson, vos remarques me donneront un sujet de conversation.