Bonjour,
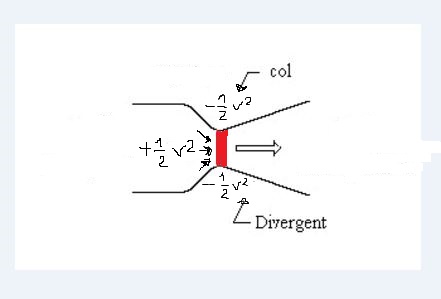
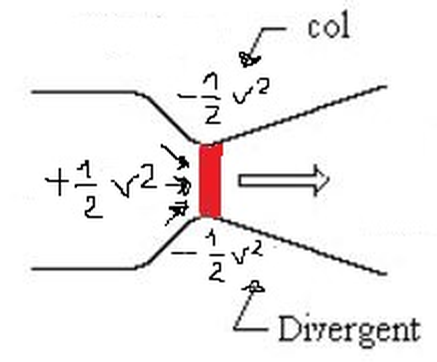
Sur le web, cette fonction représente la loi de Bernoulli "divisée par rho", c'est-à-dire amputée de la masse volumique (v²/2 + g.z + P/rho= constante).
Mais, dans les limites acceptables d'une certaine fluidité, la pression est-elle sensible à la masse volumique?
Ce que je veux dire, c'est que si l'on envoie une pression de 2 bars soit dans une barrique d'huile, soit dans du fuel lourd, cela fera toujours 2 bars de pression, non ?
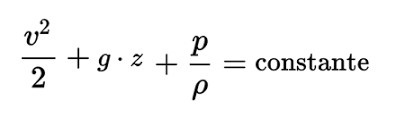
1) Bernoulli est démontré en supposant rho=Cte
2) Je dirai plutôt rho=rho(P) : la masse volumique est sensible à la pression.
Vous vous relisez parfois ou vous nous prenez vraiment pour des jambons ?Envoyé par soliris
Not only is it not right, it's not even wrong!
Merci gts2
Evidemment je parlais de liquides, pas de gaz; à propos de liquides + ou - visqueux, on m'a affirmé sur un autre forum que les pressions n'étaient pas influencés par la masse volumique.
Dernière modification par soliris ; 02/11/2019 à 17h27.
Il faut bien lire le sens de ma question: je ne demande pas si rho est influencé par la pression, mais l'inverse.
Merci
Oui mais dans le sens rho influence P, cela a un sens ambiguë.
Dans le sens P influence rho, la masse volumique est une caractéristique du matériau qui dépend de la pression qu'on lui impose, le sens est clair.
Dans l'autre sens, on peut comprendre :
- la pression au fond d'un bassin dépend de la masse volumique du fluide qui est au-dessus : évidemment oui !
- on appuie avec une force F sur un piston, la pression exercée par ce piston sur le fluide en-dessous dépend de rho(fluide) : évidemment non !
Il suffit de réécrire l'équation :
La dépendance de P par rapport à rho devient tout de suite plus évidente.
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.
J'abandonne !
Salut .
En annulant la vitesse on retrouve la formule de la pression hydrostatique qui est bien fonction de la masse volumique .Il suffit de réécrire l'équation :
Si tu envoies 2 bars , tu as 2 bars .
La réciproque est vraie aussi .
2 bars à l' endroit ou tu mesures la pression .
1 mm en dessus ou en dessous , les pressions sont différente , à cause de rot.zèd .
Je suis désolé si j'ai commis une erreur ou une méprise.
J'ai juste essayer de débloquer la situation en réécrivant l'équation donnée au 1er post.
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.
Excuses-moi, je voulais dire j'abandonne l'idée de répondre à la question, qui est soit qqch d'évident si on écrit Bernoulli comme tu l'as fait, soit une impossibilité de réponse si on s'en tient à la question initiale :
"la pression est-elle sensible à la masse volumique" précisée par "2 bars dans une barrique d'huile vs. deux bars dans du fuel lourd"
Ok, je comprends mieux. Pas de souchis alors.
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.
Merci à tous, Sethy, Dynamix, gts2, albanxiii, pour vos réponses.Il suffit de réécrire l'équation :
La dépendance de P par rapport à rho devient tout de suite plus évidente.
Tiens, c'est curieux.. J'aurais plutôt pensé que c'est la "fluidité" de la vitesse v dans la pression dynamique (donc v²/2) qui est influencée par la masse volumique, avant que ce soit la pression hydrostatique.
Cela fait quand même quelques sons de cloche différents.. Déjà on s'est rendu compte que, dans certains cas, Bernoulli tient compte de la pression cinétique (compression dans un tuyau d'eau en augmentant la vitesse), et dans d'autres de la pression "de densité" (ou plutôt "dépression" à l'extrémité du tube d'un vaporisateur).
Cela commence à faire beaucoup de modifs pour une ch'tite misère de formule, si on se dit que soit on a 2 bars de pression, quelle que soit la masse volumique, soit la masse volumique change si on change la pression.
Comme le dit Sarkozy: "vous savez, moi, pour c'que j'en dis".
Mais je prends des notes.
Dernière modification par soliris ; 04/11/2019 à 15h16.
Oui.
Oui aussi.. . . la masse volumique change si on change la pression.
Et les deux affirmations ne sont pas exclusives.
L'électronique c'est comme le violon. Soit on joue juste, soit on joue tzigane . . .
Il en tient toujours compte.
C'est quoi une pression de densité ?
... à ce point la , je suppose que tu le fais exprès .....!
2 bars , c' est une donnée (en un point) , pas une variable .
Tu sais que tu as 2 bars (tu l' as mesuré ou calculé) , peu importe ce qui l' "influence" 2 bars , c' est 2 bars , point barre .
salut.
Je suis cette discussion de loin, mais :
J'ai plutôt l'impression que tu ne saisis pas certaines choses, ce qui t'amène à douter d'une formule parfaitement claire...Cela fait quand même quelques sons de cloche différents.. Déjà on s'est rendu compte que, dans certains cas, Bernoulli tient compte de la pression cinétique (compression dans un tuyau d'eau en augmentant la vitesse), et dans d'autres de la pression "de densité" (ou plutôt "dépression" à l'extrémité du tube d'un vaporisateur)
Ces informations vous sont fournies sous réserve de vérification :)
Ok.. c'est sûrement pas la bonne expression; mais sur le fond, vous m'avez mis la puce à l'oreille ici, dans ce sujet à la réponse #2,à propos du surenfoncement du Queen Eilzabeth II, avec cette phrase : "La pression P (sous le bateau) a bien diminué parce que la pression cinétique (1/2 rho vit²) a augmenté".
Pour illustrer ce à quoi vous m'avez fait penser, voici un exemple très différent, mais il a l'avantage d'être facile à dessiner. C'est à propos de la tuyère de Laval.
Lorsque le fluide passe à l'intérieur du col, la "pression cinétique" frontale du fluide, [en + v²/2] est à son maximum quand le fluide atteint la vitesse du son; mais la réaction sur le bord interne du col induit exactement (selon votre phrase) une réaction latérale opposée, une dépression en [-v²/2], qui doit agir de façon directe, en vibrations et autres effets. Bien sûr, les ingénieurs pensent que le col subit une surpression, alors que je pense qu'il s'agit bien du contraire.
Est-ce qu'il s'agit là de l'écoulement laminaire le plus pur qui existe, à ce point que c'est la dépression qui domine ? Allez savoir, je cherche un moyen pour le montrer et donc le prouver; en fait la réponse est très simple: il faut fabriquer un col qui puisse se comprimer.
Dernière modification par soliris ; 05/11/2019 à 16h56. Motif: explications supplémentaires
1- Bernoulli concerne un fluide incompressible, ici on atteint la vitesse du son, donc incompressible ne marche plus.
2- La vitesse n'est pas maximale au niveau du col
3- ...
Bonjour,
Lorsque le fluide passe à l'intérieur du col, la "pression cinétique" frontale du fluide, [en + v²/2] est à son maximum quand le fluide atteint la vitesse du son; mais la réaction sur le bord interne du col induit exactement (selon votre phrase) une réaction latérale opposée, une dépression en [-v²/2], qui doit agir de façon directe, en vibrations et autres effets. Bien sûr, les ingénieurs pensent que le col subit une surpression, alors que je pense qu'il s'agit bien du contraire.
Le problème, c'est de prétendre opposer à égalité une cogitation solitaire à une réalisation de issue de milliers d'heures de travail d'ingénieurs, qui - eux - ont quelques connaissances en mathématiques. Consulter pour information l'article suivant.
C'est là que se trouve l'anomalie, qui ne relève ni de la mécanique des fluides, ni même de la physique en général.
Donc.. l'anomalie, c'est moi !Bonjour,
C'est là que se trouve l'anomalie, qui ne relève ni de la mécanique des fluides, ni même de la physique en général.
Alors, concernant la tuyère de Laval, en particulier, je rappelle (une fois de plus) que ceci est purement descriptif, et pas explicatif : " Lorsqu'un gaz circule à une vitesse subsonique dans un tuyau dont le diamètre se rétrécit, sa vitesse augmente. La vitesse du gaz ne peut toutefois pas dépasser celle du son (Mach 1). En effet en régime d'écoulement supersonique (vitesse supérieure à la vitesse du son) le comportement du gaz s'inverse : pour que sa vitesse augmente il faut que le diamètre du tuyau augmente (démonstration plus bas : Relation d'Hugoniot). " Même la démonstrationde Hugoniot est une bonne TROUVAILLE mais ne peut être expliquée par la relation entre les sons et le mouvement des fluides. Là-dessus, je n'ai trouvé RIEN. Alors je vous en prie, donnez-moi ce lien internet qui le montrerait, vous m'enlèveriez une douzaine de DOUTES EXISTENTIELS.
Je le répète, expliquez-moi les courbes de l'image ci-dessus. Surtout celle, au hasard, concernant la masse volumique rhô.
Bonne chance.. Au fait, ces courbes représentent chacune une fonction. Donnez-les à tous vos petits camarades du forum.
Salut,
C'est p la pression et pas rhô la masse volumique
En plus dans wikipedia c'est maqué juste en dessous. Tu devrais être un peu plus attentif.
Pour la démo en question, si ça existe.... mais j'ai ça dans mes syllabusD'autres ici feront peut-être l'effort de trouver une référence.
EDIT je laisse aussi aux autres le soins, s'ils le veulent, d'expliquer ces courbes
Dernière modification par Deedee81 ; 06/11/2019 à 15h41.
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Il y a juste besoin de trois équations classiques : détente d'un gaz adiabatique, conservation du débit massique, premier principe. Détails dans le lien ci-dessous, que vous devez connaitre puisque vous parlez de "démonstration de Hugoniot" :
https://fr.wikipedia.org/wiki/Équation_d%27Hugoniot
que voulez vous de plus ?
Pour ce qui est de l'explication des courbes :
- P diminue : la pression de sortie est plus petite que celle d'entrée
- T diminue : classique pour une détente adiabatique
- v augmente : le gaz est accéléré par le gradient de pression
et pour ce qui est de \rho on a= constante donc \rho diminue
la seule chose compliquée est pourquoi M=1 au col et pour cela vous avez Hugoniot.
