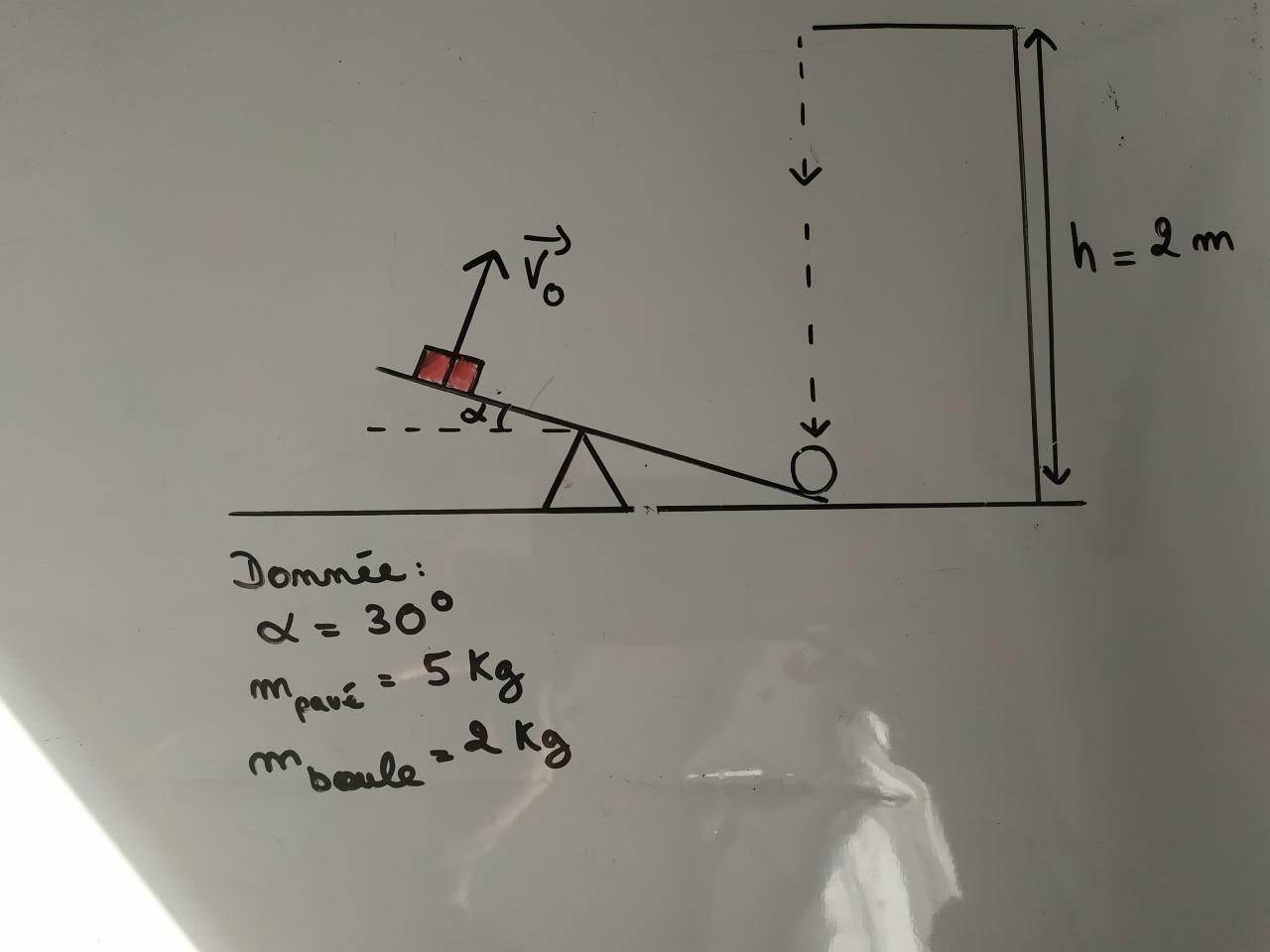
Bonjour à tous, je suis en terminal et je me suis poser un petit problème. J'aimerais déterminer l'équation de la trajectoire du pavé (cf. image ci dessous) lorsque la boule "catapulte le pavé". Pour cela j'aurai besoin de la vitesse initiale du pavé lorsqu'il est catapulté, hors je n'y parviens pas. J'ai conscience qu'on peut calculer l'énergie cinétique de la boule mais comment faire le lien avec la vitesse initiale du pavé ?
Merci d'avance pour votre aide.
Bonjour,
Approche en première approximation :
- Quelle est l'énergie mécanique de l'ensemble (m1 et m2) au moment où la masse m1 est lachée au point haut ?
- Soit Delta H, la différence d'altitude de la masse m2 entre mes 2 dessins.
Quelle est son énergie potentielle de pesanteur (sur le dessin du bas) ?
- Soit Vo, la vitesse d'expulsion de la masse m2 ...
Quelle est au même instant la vitesse de la masse m1 ?
Quelle est à cet instant la somme des énergies cinétiques des mobiles m1 et m2.
Par la conservation de l'énergie mécanique du système ... on peut alors calculer Vo.
Tout cela sans tenir compte de la déformation de la poutre de la bascule, des frottements et de ...
Un grand merci pour votre aide, alors :
- Emi (m1+m2) = Epp (m1) (car Ec et Epp de m2 sont nul au début de l'expérience)
= m1 x g x h
= 39 j
- Avec, delta H = 0,5 m, on a : Epp (m2) = m2 x g x delta H
= 24,5 j
- Lorsque m2 est expulsée, V(m1) est nul
Alors, Ec (m1+m2) = Ec (m2)
D'où, Emf (m1+m2) = Epp (m2) + Ec (m2)
= 24,5 + 1/2 x m2 x (Vo)^2
= 2,5 Vo^2 + 24,5
Or on néglige les frottements, déformations ... Donc :
Emi (m1+m2) = Emf (m1 + m2)
39 = 2,5 Vo^2 + 24,5
Vo = 2,4 m/s
J'espère que jusqu'ici cela est correcte,
On a alors, Vox = sin(Alpha) x Vo = 1,2 m/s
Voy = cos(Alpha) x Vo = 2,1 m/s
Une fois éjecté, la masse m2 n'est soumise qu'a son poids d'où:
A ( Ax=0 ; Ay=-g)
V (Vx=Vox ; Vy=-gt + Voy)
OM ( X= 1,2t ; Y= -4,9(t)^2 + 2,1t)
D'où l'équation de la trajectoire : y= -3,4x^2 + 1,75x
? j'espère que c'est juste.
Salut,
Erreur, je pense, quand tu dis : "- Lorsque m2 est expulsée, V(m1) est nul"
Juste avant que m2 décolle, m1 est encore en train de descendre (l'instant juste avant que la bascule ne touche le sol) ... et donc si les bras de la bascule sont de même longueur, la masse m1 descend à la même vitesse que la masse m2 monte.
Juste après l'impact de la bascule à butée sur le sol, l'énergie cinétique de la masse m1 qui descendait est absorbée par la déformation du sol ... mais cela on "oublie" car la masse m2 a alors décollé.
Hum... il faudrait donc que j'intègre Ec(m1) (soit 39j puisque son toute son Epp c'est transformé en Ec juste avant l'impact) au calcul de Emf(m1+m2) ? Cela me parait incohérent car auquel cas j'obtiens un vitesse Vo négative, ou alors je n'ai pas bien compris
Bonjour,
m1.g.h = m2.g.delta H + 1/2.(m1+m2)*Vo²
...
