Equation différentielle système second ordre

[automonfire]

Bonjour à tous !

Je n'arrive pas à determiner l'équation différentielle de ce système en boucle ouverte, je ne sais pas par quel "bout" commencer.

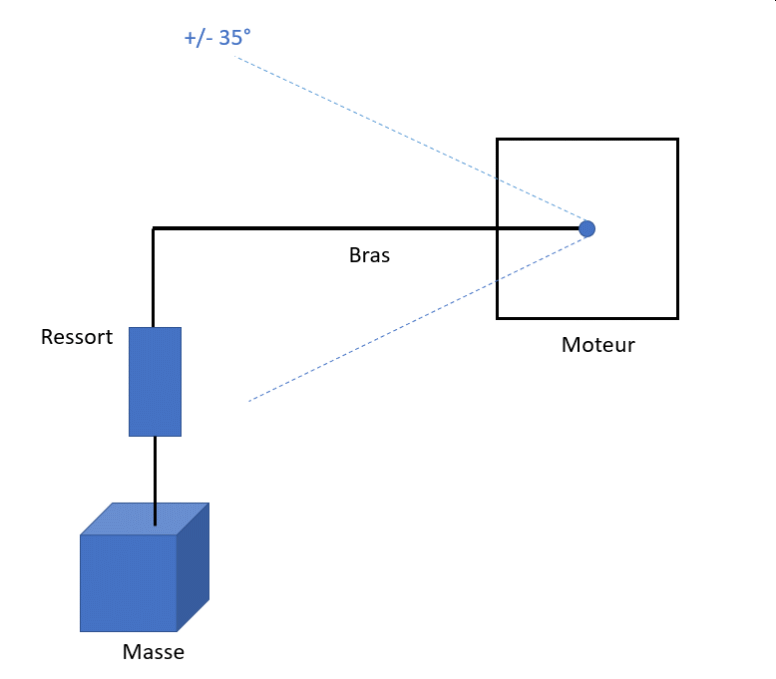
Voici le système:



Un moteur pas à pas est attaché à un support, un poids est attaché à un élastique qui lui même est attaché au bout d'un bras de longueur b fixé au moteur.
Une caméra est installée au niveau de la masse, afin de pouvoir obtenir en sortie la variation de hauteur du poids en pixels.
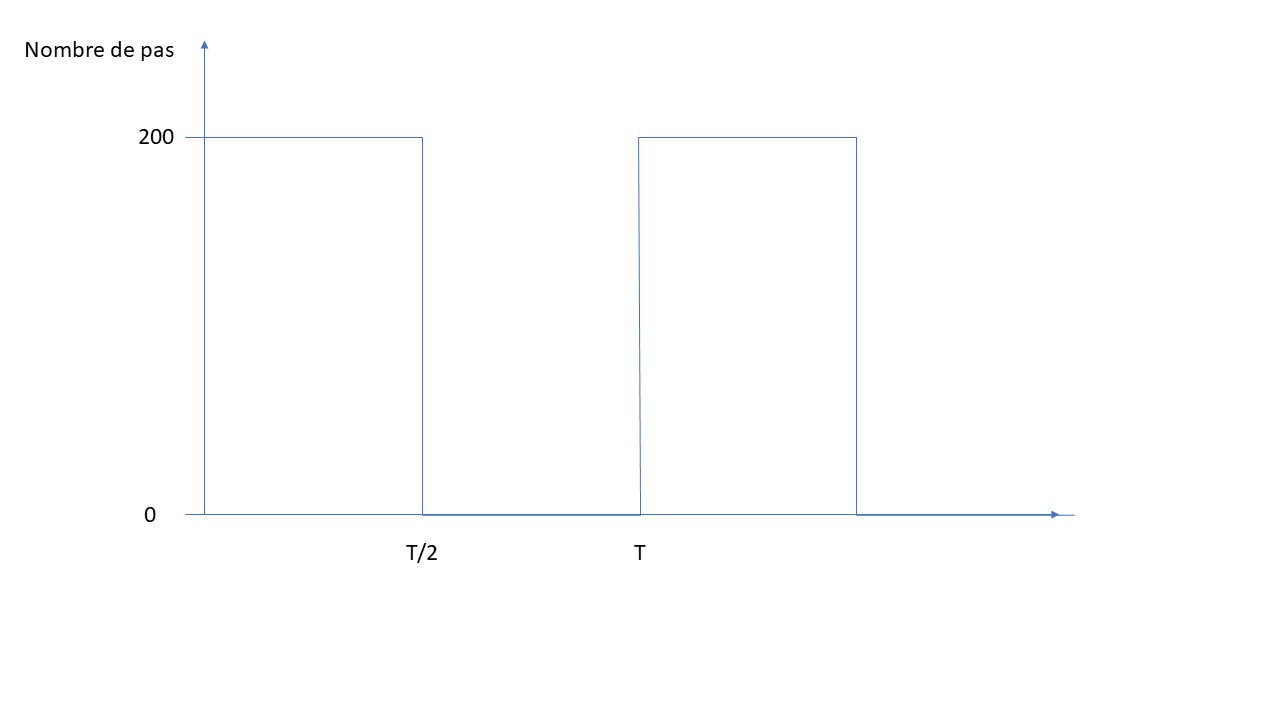
Le moteur pas à pas alterne entre 2 positions, l'angle reste faible pour négliger le fait que le poids de déplace horizontalement.

Je ne vois pas comment mettre en equation les variations de hauteur du moteur.

Votre aide me sera précieuse

Merci et à bientôt
-----

[gts2]

Bonjour,

Problème à préciser :
- si je comprends bien le bras oscille entre deux positions +-35°
- la durée de bascule entre ces deux états est-elle à prendre en compte ?
- si oui, comment est modélisé ?
- il y a une pause entre deux bascules ?
- est-ce simplement ?

[automonfire]

Bonjour,

Le bras oscille entre 2 positions, sans prendre en compte la durée de bascule entre ces 2 états.
Le moteur est piloté comme ceci:


En entrée du système il y a le nombre de pas donné en consigne au moteur pas à pas , et en sortie la variation du nombre de pixel selon y

[gts2]

Dans ce cas, c'est un système masse ressort, dans lequel il faut faire attention à ce que l'allongement du ressort fait intervenir les deux extrémités, la première liée à la masse qui est votre variable x, et la deuxième liée au bras qui aura un comportement de type signal carré.

[A voir en vidéo sur Futura]

[automonfire]

D'accord merci,
Pour modéliser le mouvement du bras, est-ce qu'il suffit de fournir en entrée un signal carré, ou bien il faut le prendre en compte dans les équations?
De plus, est-ce que le cela change le système si on remplace le ressort par un elastique?

[gts2]

Pour modéliser le mouvement du bras, est-ce qu'il suffit de fournir en entrée un signal carré, ou bien il faut le prendre en compte dans les équations ?

Il faut interpréter le texte qui n'est pas d'une précision parfaite. Je dirai oui, le mouvement du bras entrera en compte par l'amplitude du signal.

De plus, est-ce que le cela change le système si on remplace le ressort par un élastique ?

Cela ne change pas les équations

[Black Jack 2]

Bonjour,

Tel quel, l'oscillation de la masse consécutive à un mouvement (supposé instantané) du bras est non amortie ...
Sans autre précision sur T (du bras) , m et k (cte du ressort), on ne connaît ni la position ni la vitesse de la masse lors du mouvement suivant du bras... et il peut alors arriver à peu près n'importe quoi.

On peut évidemment étudier ce qui se passe en fonction du rapport de la valeur de T(bras) et de la période d'oscillation libre de la masse.